KMP算法的原理
文章目录
-
- 一、字符串匹配问题
- 二、BF算法的操作流程(暴力匹配算法)
- 三、KMP算法的操作流程
- 四、字符串的前、后缀
- 五、KMP算法的原理
- 六、KMP算法如何获取next数组?
- 七、KMP算法的代码实现
- 总结
一、字符串匹配问题
场景描述:现有两个字符串,一个被称为主串Smain,一个被称为模式串Smodel。判断Smain中是否存在某个子串(字符串中的连续片段)与Smodel完全相同。
为方便表述,我把从Smain中寻找的目标子串称为目标串Sgoal。
二、BF算法的操作流程(暴力匹配算法)
首先求出Smain和Smodel长度:int m=Smain.length(),n=Smodel.length(); 很容易想到的方法就是暴力匹配,即BF算法。 从Smain中选择一个位置start(从下标0位置开始)作为目标串Sgoal的起点,然后从左往右挨个选取字符与Smodel进行比较(指针i维护Sgoal,指针j维护Smodel)。 如果遍历的过程中出现Smain[i] != Smodel[j] 的情况,则说明以当前start为起点的Sgoal与Smodel无法完全匹配,我们就需要重新选择一个起点作为Sgoal的起始位置,然后让指针重新回到Sgoal和Smodel的起始位置(start++,i=start;j=0;),然后重新开始上述Sgoal与Smodel的匹配流程,这个操作称为回溯。 随着start的右移,如果一直没有找到Smodel而出现m-start 如果j指针顺利遍历到Smodel的末尾,则说明Smain中存在与Smodel相同的子串,且Sgoal的起始位置就是start。 暴力匹配的思路非常简单,但时间复杂度却是O(m*n),并不是一个高效的算法。 KMP算法相比BF算法的优势就在于:KMP算法把解决该类问题的时间复杂度优化到了O(n)。 KMP算法同样是挨个取字符两两比对,同样也是当j指针顺利遍历到Smodel的结尾时说明Sgoal与Smodel配对成功。不同之处在于,KMP算法的i指针不用进行回溯,这就意味着,最多只需要进行m次比较就能确定最终的结果,因此KMP算法遍历的时间复杂度是O(m)。 KMP算法的做法是: 用一个next数组记录Smodel在j位置以前的部分最长相同前、后缀的长度。即next[j]=Smodel在[0,j-1]部分最长相同前、后缀的长度。当出现 Smain[i] != Smodel[j]时,i不变,然后 j 指针回溯到next[j]对应的下标处( j =next[j]),然后从i、j位置继续往后比较。 具体操作如下图: BF做法: KMP做法: 下面,我们就来分析以下这种现象的原理。不过,我们需要先解决一个小问题: 什么是字符串的前、后缀? 字符串的前缀是指,包含首字符而不包含尾字符的子串。 字符串的后缀是指,包含尾字符而不包含首字符的子串。 根据定义,我们只需要从字符串的首字符开始往右拓展,就能得到长度不同的前缀;从字符串的尾字符开始往左拓展,就能得到长度不同的后缀; 以字符串"abcde"为例: 其前缀包括"a"、“ab”、“abc”、“abcd”;其后缀包括"e"、“de”、“cde”、“bcde”; 要讲明白KMP算法的原理,首先要解决的问题是: 为什么 j 回溯到Smodel的 j 下标以前最长相同前、后缀长度对应下标处,而 i 不变?且为什么可以直接从 i 、j位置直接往后接着遍历,而不用担心考虑 i、j以前的的部分会不匹配?这么做的原理是啥? 这就和相同前、后缀的特性有关了。 我们先回到Smain[i] 与Smodel[j] 出现不匹配的状态。 又因为i、j以前的部分完全匹配,则必然:前缀1=前缀2;后缀1=后缀2; 根据等量关系可得:前缀2=后缀1; 也就是说,如果把最长相同后缀(后缀1)作为Sgoal的开头部分,就可以直接从 i 位置和前缀2的下一位置开始往后接着配对;而前缀2的下一位置,对应的下标正是前缀2的长度值。 这就是 i 指针不变而 j 指针回溯到j以前最长相同前、后缀长度位置处,然后可以直接从 i、j位置接着往后匹配的原因。 此时最长相同后缀(后缀1)的起始位置,便是Sgoal的起始位置,用变量start_1来表示。 但此时还有一个疑问,谁能保证 [start+1,start_1 - 1] 区间内不会存在有效的起点?怎么保证start直接跳到start_1中间不会错过有效的起点? 在此,先把结论公之于众:[start+1,start_1-1] 区间内确实不存在其他有效的起点。 根据我们刚才的分析,KMP算法的实现原理就是借助了前缀2=后缀1的特性。而后缀1的起点start_1就是Sgoal的新起点。 那么,我们在选择新起点时,就只能选择所有相同前、后缀中,对应后缀1的起点。 而如果要从所有符合条件的后缀1中选择一个,将其起点作为新的start,同时又要避免错过有效的起点,就要选择所有符合条件的后缀1中起点最接近原来start的那个。 而要使得选择的后缀1的起点最接近原来的start,就要使得这个后缀1的长度最长。 这就是为什么KMP算法要选择最长相同前、后缀的原因。 因此,最长相同后缀的起点start_1,就是所有可供选择的新起点中最接近原来start的位置。换句话说,[start+1,start_1-1] 区间内不存在有效位置能作为Sgoal的起点。 截止目前,关于KMP算法的理论部分就算是搞明白了。 但还有一个难点,如何获取next数组? 难道j每遍历到一个新位置,都遍历一遍Smodel的[0,j-1]部分来获取该部分最长相同前后、缀的长度吗? 很明显,这种方式求next数组的时间复杂度至少也是O(n^2)水平,自然不可能用这种方法。 接下来,我们接着研究KMP算法如何用O(n)的时间复杂度获取next数组。 首先,我们再次明确一下next数组的含义: next数组用于记录Smodel中任意下标位置之前的子串的最长相同前、后缀的长度。 next[i]表示Smodel的[0,i-1]范围内的最长的相同前、后缀的长度。 也就是说,要求next[i],就需要在Smodel的[0,i-1]范围内寻找最长的相同前、后缀。 而这种从某个子串中寻找最长相同前、后缀的过程,和从Smain中寻找Smodel的过程极为相似。 假如把Smodel的[0,i-1]段看作_Smain,把前缀当作_Smodel,则上述寻找相同前、后缀的过程就可以看作从_Smain中寻找_Smodel的过程。只不过我们在_Smain中查找时,起点是从下标1开始,而对应的_Sgoal的最后一个字符的下标必须是i-1。 接下来先介绍一下求next数组的思路: 我们用getnext函数来获取next数组,将Smodel作为参照传入getnext函数。 用j表示[0,i-1]范围最长相同前缀的下一位置,用i表示[0,i-1]范围最长相同后缀的下一位置。则i、j之前的部分必然相同。 当Smodel[i]==Smodel[j]时,表示可以在原来最长相同前、后缀的基础上直接追加Smodel[i]和Smodel[j],同时搜索范围由原来的[0,i-1]扩大至[0,i]。 而新的最长相同前缀(Smodel的[0,j]部分)的长度为j+1。而[0,i]范围的最长相同前、后缀的长度对应的就是next[i+1]的值。因此,next[i+1]=j+1。 当Smodel[i] !=Smodel[j],表示配对失败。 之前说到过,前缀和后缀的匹配过程和从主串中查找模式串的过程及其相似。 因此,我们同样可以把j回溯到next[j]的位置。 我们分别还原一下模式串与主串匹配以及求解next数组的两个情景。 情景一:在主串中查找模式串而出现Smain[i]与Smodel[j]不匹配 此时的情形是:i、j之前的部分都相同,i位置和j位置不匹配,需要重新选择一个j位置来和i位置匹配,同时要使得新的j位置的前面部分和i位置的前面部分相同。 我们进行的操作是:让j回溯到next[j]位置。 之所以要让j回溯是因为Smodel还没遍历完,只有调整j的位置才有可能让Smain[i]与Smodel[j]重新匹配,j才有可能遍历完整个Smodel。 情景二:求next数组、遍历到i位置时出现Smodel[i] !=Smodel[j] Smodel[i] !=Smodel[j]就表示我们选择的前缀根j无法和后缀根i匹配,因此我们需要重新选择一个前缀根j来和后缀根i匹配。 此时的情形是:i、j之前的部分都相同,i位置和j位置不匹配,需要重新选择一个j位置来和i位置匹配,同时要使得新的j位置的前面部分和i位置的前面部分相同。 这不就和主串与模式串匹配而出现Smain[i]!=Smodel[j]的情景一模一样嘛! 所以我们同样采取j回溯到next[j]的方式来重新让i、j匹配,才有可能得到有效的最长前、后缀。(j、i分别表示最长相同前、后缀的后缀根) 首先是初始化。下标0和下标1前面都没有前、后缀,因此next[0]=next[1]=0; 我们从下标2开始求next数组。 要求next[2],对应的搜索范围就是[0,1],而[0,1]区间的前缀根和后缀根只能是0和1。 因此,将i、j分别初始化为1和0。 此时i、j前面的公共部分为空,正好符合j、i最长相同前、后缀的下一位置的设定。 完整代码如下: 其实求next数组有好几种不同的方式,以上是本人的习惯用法。其实求next数组的原理都是一样的,只是写法上有些不同,大家理解其中的原理就OK了。 最后对KMP算法浅浅的总结一波。 KMP算法主要分为两个步骤: 第一个步骤是求next数组,这部分的时间复杂度为O(n); 第二个步骤是遍历主串与模式串进行匹配,这部分的时间复杂度为O(m); 因此,KMP算法总督时间复杂度为O(m+n),空间复杂度为:O(n) 相比于BF算法O(m*n)的时间复杂度和O(1)的空间复杂度,在效率上有明显提升。 在此附上leetcode原题链接:https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/ 首先我们通过判断一个字符串中是否包含另一个字符串的案例引出对应的字符串匹配算法。 然后我们了解了BF算法和KMP算法的具体操作流程。 顺带了解了什么是字符串的前后缀。 重点分析了KMP算法的原理及如何求next数组,这两个是整个KMP算法中最难理解的地方。 最后完成了KMP算法的代码实现。 希望之前不太理解KMP算法的同学看完本篇能够有所收获,本篇有什么误人子弟之处也请大家帮忙指正。
如果m三、KMP算法的操作流程

观察拖拽后的上下两个字符串,发现 i、j位置以前的部分确实完全匹配。四、字符串的前、后缀
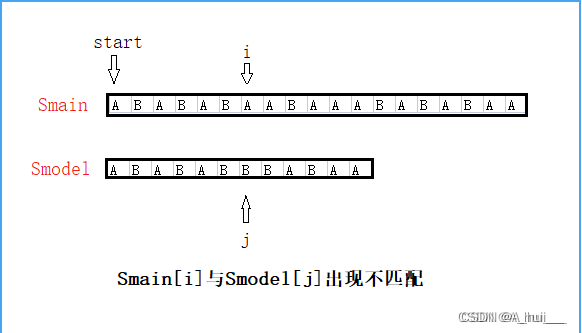
五、KMP算法的原理

根据最长相同前后缀的特性,必然有:前缀1=后缀1;前缀2=后缀2;六、KMP算法如何获取next数组?
七、KMP算法的代码实现
vector
大家可以通过这个题目练练手。总结