Sending a Sequence Over the Network

一、题目

题面翻译

你现在有一个序列 $a$，定义一个用该序列生成新序列 $b$ 的规则如下：

• 把 $a$ 这个序列分成连续的几段；
• 对于每一段，我们把这一段的长度插入到这一段的左边或右边。
• 每一段进行操作后便得到了 $b$ 序列。

比如 $a$ = $[1,2,3,1,2,3]$ ，我们可以把其分成 $[1]$，$[2,3,1]$，$[2,3]$，长度分别为 $1$，$3$，$2$。

然后我们把长度随意插入原序列中，可以得到一个不唯一的 $b$ 序列，例如：$b=[1,1,3,2,3,1,2,3,2]$。

现在给定一个长度为 $n$ $(1\le n\le 2\times 10^5)$ 已经操作后的序列 $b$ $(1\le b_i\le 10^9)$，询问你是否能构造出任意一个原序列 $a$，使得它进行如上操作后可以得到 $b$，若能构造出输出 YES，否则输出 NO。

共有 $t$ $(1\le t\le 10^4)$ 组数据，$\sum n\le 2\times 10^5$。

请注意常数可能造成的影响，否则可能会出现 TLE 等评测结果。

题目描述

The sequence $ a $ is sent over the network as follows:

1. sequence $ a $ is split into segments (each element of the sequence belongs to exactly one segment, each segment is a group of consecutive elements of sequence);
2. for each segment, its length is written next to it, either to the left of it or to the right of it;
3. the resulting sequence $ b $ is sent over the network.

For example, we needed to send the sequence $ a = [1, 2, 3, 1, 2, 3] $ . Suppose it was split into segments as follows: $ [\color{red}{1}] + [\color{blue}{2, 3, 1}] + [\color{green}{2, 3}] $ . Then we could have the following sequences:

• $ b = [1, \color{red}{1}, 3, \color{blue}{2, 3, 1}, \color{green}{2, 3}, 2] $ ,
• $ b = [\color{red}{1}, 1, 3, \color{blue}{2, 3, 1}, 2, \color{green}{2, 3}] $ ,
• $ b = [\color{red}{1}, 1, \color{blue}{2, 3, 1}, 3, 2, \color{green}{2, 3}] $ ,
• $ b = [\color{red}{1}, 1,\color{blue}{2, 3, 1}, 3, \color{green}{2, 3}, 2] $ .

If a different segmentation had been used, the sent sequence might have been different.

The sequence $ b $ is given. Could the sequence $ b $ be sent over the network? In other words, is there such a sequence $ a $ that converting $ a $ to send it over the network could result in a sequence $ b $ ?

输入格式

The first line of input data contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases.

Each test case consists of two lines.

The first line of the test case contains an integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the size of the sequence $ b $ .

The second line of test case contains $ n $ integers $ b_1, b_2, \dots, b_n $ ( $ 1 \le b_i \le 10^9 $ ) — the sequence $ b $ itself.

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case print on a separate line:

• YES if sequence $ b $ could be sent over the network, that is, if sequence $ b $ could be obtained from some sequence $ a $ to send $ a $ over the network.
• NO otherwise.

You can output YES and NO in any case (for example, strings yEs, yes, Yes and YES will be recognized as positive response).

样例 #1

样例输入 #1

7
9
1 1 2 3 1 3 2 2 3
5
12 1 2 7 5
6
5 7 8 9 10 3
4
4 8 6 2
2
3 1
10
4 6 2 1 9 4 9 3 4 2
1
1

样例输出 #1

YES
YES
YES
NO
YES
YES
NO

提示

In the first case, the sequence $ b $ could be obtained from the sequence $ a = [1, 2, 3, 1, 2, 3] $ with the following partition: $ [\color{red}{1}] + [\color{blue}{2, 3, 1}] + [\color{green}{2, 3}] $ . The sequence $ b $ : $ [\color{red}{1}, 1, \color{blue}{2, 3, 1}, 3, 2, \color{green}{2, 3}] $ .

In the second case, the sequence $ b $ could be obtained from the sequence $ a = [12, 7, 5] $ with the following partition: $ [\color{red}{12}] + [\color{green}{7, 5}] $ . The sequence $ b $ : $ [\color{red}{12}, 1, 2, \color{green}{7, 5}] $ .

In the third case, the sequence $ b $ could be obtained from the sequence $ a = [7, 8, 9, 10, 3] $ with the following partition: $ [\color{red}{7, 8, 9, 10, 3}] $ . The sequence $ b $ : $ [5, \color{red}{7, 8, 9, 10, 3}] $ .

In the fourth case, there is no sequence $ a $ such that changing $ a $ for transmission over the network could produce a sequence $ b $ .

二、分析

对于每一个a[i]来说，它可以是上一段的长度，也可以是下一段的长度。
那么就有这两种情况
Case1：这是一个长度标志，放在这段子序列的左边
那么只需要看dp[i-1]是否满足条件，if(dp[i-1]) dp[i+a[i]]=1;
Case2：这是一个长度标志，放在这段子序列的右边
那么只需要看dp[i-a[i]-1]是否满足条件，if(dp[i-a[i]-1]) dp[i]=1;

以样例1为例：
初始化

循环for(int i=1;i<=n;i++)
i=1

i=3

…

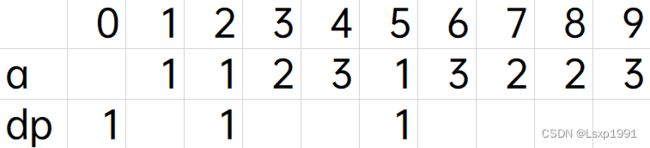
代码：

#include
#include
using namespace std;
const int N=2e5+10;
int n,a[N];
bool dp[N];
int main()
{
    int T;cin>>T;
    while(T--)
    {
        int n;cin>>n;
        for(int i=1;i<=n;i++) cin>>a[i];
        memset(dp,0,sizeof(dp));
        dp[0]=1;
        for(int i=1;i<=n;i++)
        {
            //Case1:In the left
            if(i+a[i]<=n)
            {
                if(dp[i-1]) dp[i+a[i]]=1;
            }
            //Case2:In the right
            if(i-a[i]-1>=0)
            {
                if(dp[i-a[i]-1]) dp[i]=1;
            }
        }
        if(dp[n]) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;     
    }
}