数据结构——顺序栈【c语言版】
栈(stack)是一种只能在一端插入或删除操作的线性表。(既操作受限的线性表)
栈只能在表尾插入或删除元素,表尾就是栈的栈顶,表头就是栈底
栈的主要特点:LIFO(last in first out) "后进先出"
栈可以采用顺序存储结构(顺序栈)和链式存储结构(链式栈)
下面是采用顺序存储结构来实现的顺序栈
假设栈的元素个数最大不超过正整数MAXSIZE,所以元素具有同一数据类型(ElemType),用下来方式来声明顺序栈的类型SQStack:
#define MAXSIZE 128
typedef int ElemType;
typedef struct
{
ElemType data[MAXSIZE];//存储栈的元素值
int top;//存储栈顶元素的下标(栈顶指针元素)
}SQStack;
对于顺序栈来说,有四个非常重要的要素
1.栈空条件:s.top==-1
2.栈满条件:s.top==MAXSIZE-1
3.进栈操作: s.top=s.top+1;
s.data[s.top]=e;
或 s.data[s.top+1]=e;
s.top=s.top+1;
4.出栈操作: *e=s.data[s.top];
s.top=s.top-1;
或 s.top=s.top-1;
*e=s.data[s.top+1];
1) 栈的初始化
创建一个空栈,让栈顶指针指向-1,代码如下:
SQStack InitStack()
{
SQStack s;
s.top = -1;
return s;
} 因为顺序栈采用数组来实现,而数组的大小已经给定,所以,不需要申请内存。
2)销毁栈
顺序存储不存在销毁操作,但是我们为了规范,依然给出了销毁栈的函数,不过没有如何操作,代码如下:
/*
顺序存储不存在销毁操作
*/
void DestroyStack(SQStack *s)
{
}3)判断栈是否为空
判断栈是否为空是需要判断s.top是否等于-1即可,代码如下:
int StackEmpty(SQStack s)
{
if(s.top == -1)
{
return 1;
}
else
{
return 0;
}
}如果你觉得上述代码太过于繁琐,也可以这样写:
int StackEmpty(SQStack s)
{
return (s.top == -1);
}4)进栈(push)
进栈,也称入栈,执行该操作需要先判断栈是否已满,避免栈上溢,代码如下:
/*
满:s.top==MAXSIZE-1
进栈操作:
s.top=s.top+1;
s.data[s.top]=e;
若栈不满,进行相关操作,并返回1;
否则,提示,返回0
*/
int Push(SQStack *s,ElemType e)
{
if(s->top != MAXSIZE-1)
{
s->top = s->top + 1;
s->data[s->top] = e;
return 1;
}
else
{
return 0; //栈满,既栈上溢
}
} 5)出栈(Pop)
出栈,也称退栈,执行该操作需要先判断栈是否为空,避免栈下溢,代码如下:
/*
出栈操作:
*e=s.data[s.top];
s.top=s.top-1;
若栈不空,进行相关操作,并返回1;
否则,提示,返回0
*/
int Pop(SQStack *s,ElemType *e)
{
if(s->top != -1)
{
*e = s->data[s->top];
s->top = s->top - 1;
return 1;
}
else
{
return 0; //栈空,既栈下溢
}
} 6)取栈顶元素
取栈顶元素也需要,判断栈是否为空,以确保操作合法性,代码如下:
/*
取栈顶元素操作:
*e=s.data[s.top];
若栈不空,进行相关操作,并返回1;
否则,提示,返回0
*/
int GetTop(SQStack s,ElemType *e)
{
if(s.top != -1)
{
*e = s.data[s.top];
s.top = s.top - 1;
return 1;
}
else
{
return 0;
}
}
7)输出栈(从栈底到栈顶)
/*
从栈底 至 栈顶
0---s.top
*/
void display(SQStack s)
{
int i;
printf("栈的元素为:");
for(i=0;i<=s.top;i++)
{
printf("%d ",s.data[i]);
}
printf("\n");
}下面是入栈和退栈的操作,代码如下:
int main()
{
SQStack s;
s = InitStack();
int i;
for(i=1;i<=7;i++)
{
Push(&s,i); //将1--7一次入栈
}
ElemType *e;
Pop(&s,&e); //将栈顶元素出栈
display(s); //输出栈的元素(从栈底到栈顶)
return 1;
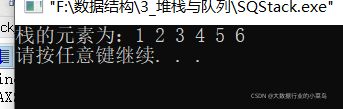
} 测试结果如下:
最后在附上完整代码:
#include
#define MAXSIZE 128
typedef int ElemType;
typedef struct
{
ElemType data[MAXSIZE];//存储栈的元素值
int top;//存储栈顶元素的下标
}SQStack;
/*
空:s.top==-1
满:s.top==MAXSIZE-1
进栈:
s.top=s.top+1;
s.data[s.top]=e;
-----------------
s.data[s.top+1]=e;
s.top=s.top+1;
出栈:
*e=s.data[s.top];
s.top=s.top-1;
-----------------
s.top=s.top-1;
*e=s.data[s.top+1];
取栈顶元素:
*e=s.data[s.top];
输出:0----s.top
*/
/*
1.初始化
空:s.top==-1
*/
SQStack InitStack()
{
SQStack s;
s.top = -1;
return s;
}
/*
2.销毁
顺序存储不存在销毁操作
*/
void DestroyStack(SQStack *s)
{
}
/*
3.判断栈是否为空
若为空,返回1;
否则,返回0
*/
int StackEmpty(SQStack s)
{
return (s.top == -1);
}
/*
4.进栈
满:s.top==MAXSIZE-1
s.top=s.top+1;
s.data[s.top]=e;
若栈不满,进行相关操作,并返回1;
否则,提示,返回0
*/
int Push(SQStack *s,ElemType e)
{
if(s->top != MAXSIZE-1)
{
s->top = s->top + 1;
s->data[s->top] = e;
return 1;
}
else
{
return 0;
}
}
/*
5.出栈
*e=s.data[s.top];
s.top=s.top-1;
若栈不空,进行相关操作,并返回1;
否则,提示,返回0
*/
int Pop(SQStack *s,ElemType *e)
{
if(s->top != -1)
{
*e = s->data[s->top];
s->top = s->top - 1;
return 1;
}
else
{
return 0;
}
}
/*
6.取栈顶元素
*e=s.data[s.top];
若栈不空,进行相关操作,并返回1;
否则,提示,返回0
*/
int GetTop(SQStack s,ElemType *e)
{
if(s.top != -1)
{
*e = s.data[s.top];
s.top = s.top - 1;
return 1;
}
else
{
return 0;
}
}
/*
7.输出
从栈底 至 栈顶
0---s.top
*/
void display(SQStack s)
{
int i;
printf("栈的元素为:");
for(i=0;i<=s.top;i++)
{
printf("%d ",s.data[i]);
}
printf("\n");
}
int main()
{
SQStack s;
s = InitStack();
int i;
for(i=1;i<=7;i++)
{
Push(&s,i); //将1--7一次入栈
}
ElemType *e;
Pop(&s,&e); //将栈顶元素出栈
display(s); //输出栈的元素(从栈底到栈顶)
return 1;
}