CS224n 2019 Winter 笔记（一）：Word Embedding:Word2vec and Glove

摘要

笔记只记个人学习重点和难点，不追求全面，只做读书过程中的疑惑解释，既做个人心得记录，也供读者参考
如有错误，烦请留言指点，谢过！
如有错误，烦请留言指点，谢过！
如有错误，烦请留言指点，谢过！

本次课Manning教授重点介绍CBOW模型和Glove模型，并为CBOW模型的目标函数做随机梯度下降推导。笔记主要记录CBOW和Skip-Gram两种模型主要流程及有关细节，顺带提一下Glove（推荐一篇博文以助理解）。

一、语言模型（Language Model）

在基于统计概率的自然语言处理中，如果把每个单词看成一个单独的离散变量，句子就是多个变量同时发生的结果，因此就有了不同的语言模型。

下面以句子> The cat jumped over the puddle为例说明两个模型

（一）一元模型（Unary Language Model）

如果把每个单词看成一个单独的离散变量，句子就是多个变量同时发生的结果，那么一个句子出现的概率可以写成：$$P(w_1,w_2,\dots ,w_n)$$

一元模型中，将句子中的所有单词都看成是独立变量，单词在所有文档中出现的概率是固定且独立的。因此$$P(w_1,w_2,\dots ,w_n)=\prod _{i=1}^{n}P(w_i)$$

但是，这个模型完全忽略了单词与单词之间的联系。比如，把某些语法固定搭配的单词同时出现的概率描述成相互独立显然是不合适的。如："I am a teacher"的概率显然会比"you appel economy war"的概率要高，因为第一个句子是符合语法的、有含义的，而第二个句子是混乱的、无意义的。

（二）二元模型（Bigram Model）

二元模型中，考虑了单词之间的耦合性，以条件概率的形式描述句子的出现概率$$P(w_1,w_2,\dots ,w_n)=\prod _{i=2}^{n}P(w_i|w_{i-1})$$

二、如何表示“word”——词向量（Word Vector）

如何表示一个单词或者汉字，是自然语言处理中的关键问题。最简单的词表示方法是“one-hot”（独热），它使用整个词汇表的大小作为词向量维度。向量的非常稀疏，只有一个1（词在词汇表出现的位置对应于向量的index上的值为1），其余全为0。

在cs224n官方给的notes中，这么定义one-hot：

One-hot vector: Represent every word as an ${\mathbb{R}}^{|V|\times 1}$ vector with all 0s and one 1 at the index of that word in the sorted english language.

举个例子：在长度为5000的vocabulary中，"bank"这个单词在词汇表中是第3个词，那么它的one-hot表示可以表示为
$$\begin{array}{c}[0,0,1,0,\cdots ,0]\\ 5000\end{array}$$
这种词向量表示方法有几个比较大的缺点：

• 向量的元素中，只有一个1，其余全是0，使得向量维数极大且极其稀疏（高维稀疏）
• 每一个词映射到高维空间都是相互正交的，也就是说one-hot向量空间中词与词之间没有任何联系，或者说无法通过词向量来判断出他们之间是否有联系，无法表达词与词之间的关系，如近义词、反义词等等
• 无法描述句子与句子、词与词之间的相似度
• 无法处理一词多义的情况

三、Word2Vec模型

2013年Mikolov在NIPS 2013中提出了Word2Vec（附报告PPT下载），旨在将所有的词向量化，就可以定量的去度量词与词之间的关系，甚至挖掘词之间的内在联系。引用课程assignment 2的handout中的一句话来描述其思想：

The key insight behind word2vec is that ‘a word is known by the company it keeps’.

Word Embedding and Word2vec
需要说明，word embedding是一个将词向量化的概念，是一个统称，而word2vec是谷歌的大神Mikolov提出的一种基于分布假设（认为上下文环境相同的词语其语义也相似）的word embedding的具体实现方法，能将高维稀疏的one-hot向量转化为低维稠密向量，具有相似语义的单词的向量之间距离较小，部分词语之间的关系能够用向量的运算表示。

（一）Word2vec的作用

Word2vec从词的内涵出发，认为词的含义可以从词的上下文推测出来，同义的词应该具有类似的上下文。同时，也能较为方便的计算词的相似度。

先明确一点，Word2Vec模型的作用是将英文、汉语、日文、韩文等等字符转化为一系列的向量（就是word to vector的意思），利用这些向量，MLer们可以做各种有意思的东西，最简单的比如计算句子/词语的相似度，做词语聚类。因为有了这个向量的存在，人们才能对一个词语或者句子进行量化，转化为一系列数字，再通过各种技术做各种各样有意思的任务。

word2vec其实就是一种把word变为vector的技术。怎么变呢？假设一个单词"China"，表示为$w^{\prime }$，词汇表（vocabulary）$V$的大小为$\left|V\right|$，所以用one-hot表示"China"就是：$$\begin{array}{c}{\left[0,\cdots ,0,1,0,\cdots ,0\right]}^T\\ \left|V\right|\end{array}$$

训练word2vec模型的目的就是找出一个转换矩阵$W$，通过与$w^{\prime }$相乘得到词对应的词向量$w$，计算过程为：$$w=W{w}^{\prime }$$转换矩阵$W$在模型设计中可自定义，假设是 $p\times \left|V\right|$，那么词向量$w$就是$p$的向量（如果这个看不明白，请结合CBOW模型，$W$就是输入层到隐层的参数矩阵）。

因此，word2vec最终目的就是为了得到这个转换矩阵（当然，还有另一个从隐层到输出层的参数矩阵，也是我们想要的矩阵），而这个转换矩阵就是训练的参数矩阵。

下面，具体介绍Word2Vec模型，它主要有Skip-Gram和CBOW两种，Skip-Gram是给定input word来预测上下文。而CBOW是给定上下文，来预测input word，两者互为镜像。

这里需要注意一点，Skip-Gram和CBOW两种模型都是word2vec的实现方法，都是为了将word表示成vector的模型，区别就是二者思考的角度（训练过程）不一样，一个通过中心词预测上下文的方法训练出词向量，一个是通过上下文预测中心词的方法训练出词向量。

（二）Continuous Bag of Words Model (CBOW)

1、CBOW模型思想

CBOW的目的是通过中心词（center word）的上下文（context）来预测该中心词，其训练输入是所有上下文对应的词向量，输出是某单个词的词向量。
比如下面这段话：

government debt problems turning into banking crises as happened in 2009

如果上下文窗口大小为2（即在中心词左右两边选择最近的2个词，共计4个，作为上下文），特定的这个词（中心词）是”banking ”，也就是我们需要的输出向量。那么这上下文4个词对应的one-hot向量就是模型的输入，对应的CBOW模型输入层有4个神经元。而模型的输出是所有词的softmax概率（当然，我们希望的是中心词的概率最大）。

由于CBOW使用的是词袋模型，因此这4个词都是平等的，也就是不考虑这些词和中心次之间的距离大小，只要在上下文窗口之内即可。

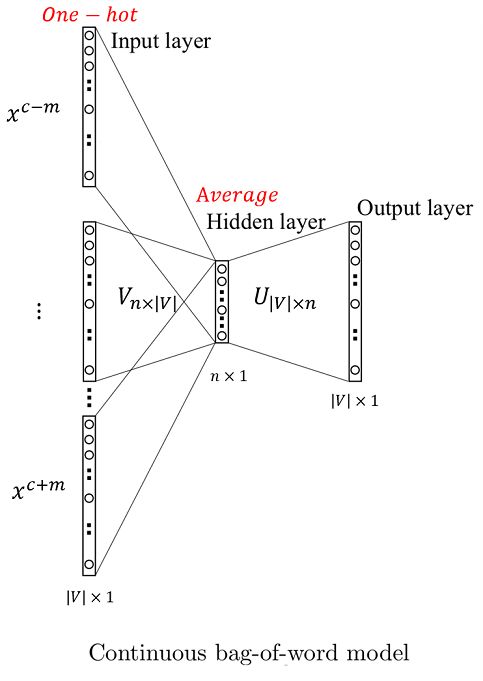
模型工作流程如下（如模型示意图所示）：

1. 设中心词是句子中的第$c$个词，上下文窗口大小（window size）为$m$。对$2m$个上下文单词生成其对应的$2m$个one-hot向量：$\left\{x^{(c-m)},\cdots ,x^{(c-1)},x^{(c+1)},\cdots ,x^{(c+m)}\right\}$，每个one-hot向量都是$\left|V\right|$维的，$\left|V\right|$为词汇表（vocabulary）大小；
2. 通过与初始化后的矩阵${\mathcal{V}}_{n\times |V|}$相乘，生成$2m$个$n$维向量$\left\{v_{c-m},\cdots ,v_{c-1},v_{c+1},\cdots ,v_{c+m}\right\}$，其中：$$v_{c-m}=\mathcal{V}{x}^{(c-m)},\cdots ,v_{c-1}=\mathcal{V}{x}^{(c-1)},v_{c+1}=\mathcal{V}{x}^{(c+1)},\cdots ,v_{c+m}=\mathcal{V}{x}^{(c+m)}$$
3. 对这$2m$个$n$维向量求平均，得均值向量$$\hat{v}=\frac{v_{c-m}+v_{c-1}+v_{c+1}+v_{c+m}}{2m}$$
4. 将这个均值向量与向量 ${\mathcal{U}}_{|V|\times n}$相乘，得到一个$\left|V\right|$维向量：$z=\mathcal{U}\hat{v}$
5. 最后将这个低维稠密向量通过softmax函数转化为以概率值为元素的$\left|V\right|$维向量：$\hat{y}=softmax(z)$
   

既然有了模型，那就应该还有目标函数或者损失函数，用来指导训练过程。回到上面的句子，中心词是"banking"，上下文是"turning"、“into”、“crises”、“as”，在CBOW中，"banking"就是输入，“turning”、“into”、“crises”、"as"就是标签（注意，不是输出），而模型的输出就是要不断的接近标签值。

此外，我们注意到输出是一个向量，元素值是概率值，所以我们的目标函数就可以设为标签和输出之间的概率分布的差异度，目标就是最小化差异度。官方notes用“交叉熵”来衡量，即$$H(\hat{y},y)=-\sum _{i=1}^{|V|}{y}_i\log ({\hat{y}}_i)$$

（三）Skip-Gram Model

模型工作流程如下（如模型示意图所示，请参考：skip-gram,单词向量化算法及其数学原理）：

1. 设中心词是句子中的第$c$个词，上下文窗口大小为$m$。以中心词的one-hot向量$x_c$作为输入，维度是$\left|V\right|\times 1$
2. 通过与初始化后的矩阵${\mathcal{U}}_{n\times |V|}$相乘，生成一个$n$维向量：$$v=\mathcal{U}\cdot x_c$$
3. 从hidden layer 到 Output layer 做了$2m$次的前向传递，每次的传递都与相同的权重矩阵 ${\mathcal{V}}_{|V|\times n}$ 的一个行向量进行点乘（这一点在很多博客、帖子中都没有讲清楚，需要注意。但是在cs224n 2019 winter的第二个视频（B站）的开头，我们的Manning教授就解释清楚了），产生$\left|V\right|$个值$\left\{{\hat{y}}_1,\cdots ,{\hat{y}}_{|V|}\right\}$：
   $$\mathcal{V}=\left[\begin{array}{c}{\mathcal{V}}_1\\ ⋮\\ {\mathcal{V}}_{|V|}\end{array}\right],{\hat{y}}_i=v\cdot {\mathcal{V}}_i$$
4. 将这$2m$次所产生的值 ${\hat{y}}_1$ 到 ${\hat{y}}_{2m}$ 通过Softmax函数转换成概率值：
   $$y_i=\frac{{\hat{y}}_i}{{\sum }_i^{|V|}{\hat{y}}_i}$$这里要注意的是，Softmax 分母的计算是由每一个 ${\hat{y}}_i$ 值而来，每个${\hat{y}}_i$都有可能是负数，但经softmax转换后，都是介于0到1之间的数值。

四、负采样（Negative Sampling）

（一）什么是负采样

（二）为什么要负采样？或者说，负采样的作用是什么？

CS224n官方的slide和note都没有说清楚为什么要用负采样，负采样到底有什么作用，只是在推导公式没有相应的深入分析。经过查阅资料，终于解惑，也记录下来。

先来看一段知乎的解释：

训练一个神经网络意味着要输入训练样本并且不断调整神经元的权重，从而不断提高对目标的准确预测。每当神经网络经过一个训练样本的训练，它的权重就会进行一次调整。

正如我们上面所讨论的，vocabulary的大小决定了我们的Skip-Gram神经网络将会拥有大规模的权重矩阵，所有的这些权重需要通过我们数以亿计的训练样本来进行调整，这是非常消耗计算资源的，并且实际中训练起来会非常慢。

负采样（negative sampling）解决了这个问题，它是用来提高训练速度并且改善所得到词向量的质量的一种方法。不同于原本每个训练样本更新所有的权重，负采样每次让一个训练样本仅仅更新一小部分的权重，这样就会降低梯度下降过程中的计算量。

上面的描述基本说到点上了，但是仍然不是特别直观。下面，我们直接从公式中分析。

首先，先来看不用负采样方法的时候，算法是如何工作的：

（1）不用负采样时，由数值转化为概率值时用的函数时softmax（公式来源于CS224n官方的notes，戳这里下载）
$$\min J=-\log \frac{\exp (u_c^T\hat{v})}{{\sum }_{j=1}^{|V|}\exp (u_j^T\hat{v})}$$
可以看到，在优化$J$时每次迭代都需要把所有$1,2,\cdots ,\left|V\right|$的$u_j^T\hat{v}$相加求和，这就不可避免的要对每个$j$计算向量点乘——$u_j^T\hat{v}$，当$\left|V\right|$很大时（即vocabulary很大），这个计算量是很恐怖的。
所以，在负采样中舍弃了softmax函数，采用了sigmod函数：
$$\sigma (v_c^T{v}_w)=\frac{1}{1+\exp (v_c^T{v}_w)}$$
（2）再引用官方notes中对$u_j$的描述：

$u_i$:$i$-th row of $\mathcal{U}$, the output vector representation of word $w_i$

根据（1）中所描述，每次迭代时都要计算向量点乘——$u_j^T\hat{v}$，就相当于更新整个参数矩阵$\mathcal{U}$。

对此，负采样可以很有效的避免整个矩阵的无效更新，因为负采样设立的新的目标函数中，采用的sigmod函数只需要部分$u_i$，请看公式：
$$\begin{gathered} J=-\sum _{(w,c)\in D}\log \frac{1}{1+\exp (-u_w^T{v}_c)}-\sum _{(w,c)\in \tilde{D}}\log \frac{1}{1+\exp (u_w^T{v}_c)} \\ =-\log \sigma \left(u_{c-m+j}^T\cdot v_c\right)-\sum _{k=1}^K\log \sigma \left(-{\tilde{u}}_k^T\cdot v_c\right) \end{gathered}$$

来分析一下这个公式，目标是$\min J$，公式第一行等号右侧第二项的求和号下方：$(w,c)\in \tilde{D}$，这个的意思是在“负样本”中选择一部分来进行更新迭代。

那么，这一部分有多少词呢？来看公式第二行，右侧第二项求和号的上标是$K$，这就是采样的负样本的数量。每个负样本都是一个词，每个词的向量表示都是$\mathcal{U}$的其中一行（根据定义）。

所以这个公式告诉我们，负采样只更新了权重矩阵的部分行，也就是只更新了部分参数，大大减小了计算量。

综上所述，负采样最主要作用就是减小训练计算量，加快训练速度。

五、Glove（Global Vectors for Word Representation）

2014年斯坦福大学的Pennington在EMNLP中提出了Glove模型（CS224n授课教授Manning是三作），Glove是基于Word2vec提出的词向量模型。要理解其思想，首先得先介绍作者自己分类的两种模型：（1）Matrix Factorization Methods，基于矩阵分解的方法（2）Shallow Window-Based Methods，基于上下文窗口的方法。

而LSA(Latent semention analysis)和HAL(Hyperspace Analogue to Language)是基于矩阵分解的方法的代表。LSA、HAL是基于矩阵分解（或者说是基于计数的，因为分解的共现矩阵co-occurrence matrix正是计算word出现次数的矩阵）的方法，利用的是全局统计信息，但在word相似性等方面表现不好

Word2vec是基于shallow window的，学习上下文窗口的预测，展示了捕捉复杂语言模式的能力，而不仅仅是单词相似性，但没有利用全局统计信息

在此基础上，作者结合了这两种方法的有点进一步改进而提出了Glove模型，具体模型细节这里不展开，推荐两个博客，将论文中的目标函数的演变过程讲的比较细致：

1、论文阅读《GloVe: Global Vectors for Word Representation》
2、Glove

六、提问

1、不论是CBOW还是Skip-Gram中，都有两个参数矩阵 $\mathcal{U}$ 和 $\mathcal{V}$ ，这两者是不是互为转置？如果不是，那么每个单词是不是就有两种表示了？
答：两者不互为转置，是两个不同的矩阵。因此，每个单词其实是有两种表示的，每种都是一个向量，可以将两个向量相加或者做其他操作变成另一个向量，然后这个向量就可以表示这个词了。

2、负采样中，每次更新部分的参数，这样不是应该更慢吗？一次更新的多一点的参数不好吗？一点一点挤牙膏难道还能更快？
这个问题答案其实也很明显，当模型训练好时，其输出是一个one-hot的向量，值为1的位置，对应的就是vocabulary相应位置的词（就是我们希望的词，即正样本），而0值对应的就是负样本了。

而我们也知道，输出的one-hot向量的每个位置都对应这一个vocabulary中的词，也对应这权重矩阵$\mathcal{U}$的其中一行。因此在迭代更新权向量时，针对0值对应着的权重矩阵的那些行向量的更新迭代都是基本都是不起作用的，因此这部分计算量正好被负样本节省出来了。

Reference

1. 通俗易懂理解——Skip-gram的负采样
2. Word2Vec介绍: 为什么使用负采样（negtive sample）？
3. Word2Vec原理之负采样算法
4. 关于Word2Vec的一些总结
5. 论文阅读《GloVe: Global Vectors for Word Representation》