Prim+Kruskal（最小生成树）

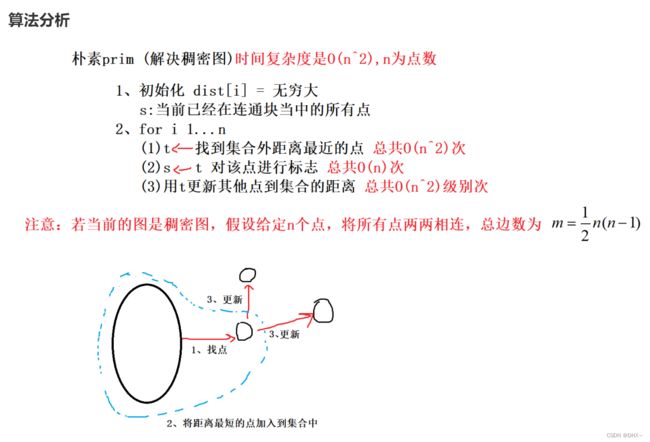
Prim算法求最小生成树

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

1≤n≤500
1≤m≤10^5
图中涉及边的边权的绝对值均不超过 10000。

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

6

 

#include
#include
using namespace std;
const int N=550,INF=0x3f3f3f3f;
int g[N][N];
int dist[N];
bool st[N];
int n,m;
int prim()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    int res=0;
    for(int i=0;idist[j])) t=j;
        //判断是否是孤立点
        if(dist[t]==INF) return INF;
        st[t]=1;
        res+=dist[t];
        //用t更改其他点到集合的距离
        for(int j=1;j<=n;j++)
        {
            if(dist[j]>g[t][j]&&!st[j])
            dist[j]=g[t][j];
        }
    }
    return res;
}
int main()
{
    cin>>n>>m;
    memset(g,0x3f,sizeof g);
    while(m--)
    {
        int a,b,c;cin>>a>>b>>c;
        g[a][b]=g[b][a]=min(g[a][b],c);
    }
    int t=prim();
    if(t==INF) cout<<"impossible"<

  Kruskal算法求最小生成树

#include
#include
using namespace std;
const int N=2e5+10;
struct Edge
{
    int a,b,w;
}stu[N];
int p[N];
int n,m;
int cmp(Edge x,Edge y)
{
    return x.w>n>>m;
    for(int i=0;i>stu[i].a>>stu[i].b>>stu[i].w;
    sort(stu,stu+m,cmp);
    Kru();
    return 0;
}

局域网

某个局域网内有 n 台计算机和 k 条 双向(无向图) 网线，计算机的编号是 1∼n。由于搭建局域网时工作人员的疏忽，现在局域网内的连接形成了回路，我们知道如果局域网形成回路那么数据将不停的在回路内传输，造成网络卡的现象。

注意：

• 对于某一个连接，虽然它是双向的，但我们不将其当做回路。本题中所描述的回路至少要包含两条不同的连接。
• 两台计算机之间最多只会存在一条连接。
• 不存在一条连接，它所连接的两端是同一台计算机。

因为连接计算机的网线本身不同，所以有一些连线不是很畅通，我们用 f(i,j) 表示 i,j  之间连接的畅通程度，f(i,j) 值越小表示 i,j 之间连接越通畅。

现在我们需要解决回路问题，我们将除去一些连线，使得网络中没有回路且不影响连通性（即如果之前某两个点是连通的，去完之后也必须是连通的），并且被除去网线的 Σf(i,j) 最大，请求出这个最大值。

输入格式

第一行两个正整数 n,k。

接下来的 k 行每行三个正整数 i,j,m 表示 i,j 两台计算机之间有网线联通，通畅程度为 m。

输出格式

一个正整数，表示被除去网线的 Σf(i,j) 的最大值(求最小生成树）。

数据范围

1≤n≤100
0≤k≤200
1≤f(i,j)≤1000

输入样例：

5 5
1 2 8
1 3 1
1 5 3
2 4 5
3 4 2

输出样例：

8

 

#include
#include
#include
using namespace std;
const int N=210;
int p[N];
int n,m;
struct Edge
{
    int a,b,w;
}stu[N];
int cmp(Edge x,Edge y)
{
    return x.w>n>>m;
    for(int i=1;i<=m;i++) cin>>stu[i].a>>stu[i].b>>stu[i].w;
    sort(stu+1,stu+1+m,cmp);
    unit();
    int res=0;
    for(int i=1;i<=m;i++)
    {
        int x=stu[i].a,y=stu[i].b,ww=stu[i].w;
        if(find(x)!=find(y)) p[find(x)]=find(y);
        else res+=ww;
    }
    cout<

连接格点

有一个 m 行 n 列的点阵，相邻两点可以相连。

一条纵向的连线花费一个单位，一条横向的连线花费两个单位。

某些点之间已经有连线了，试问至少还需要花费多少个单位才能使所有的点全部连通。

输入格式

第一行输入两个正整数 m 和 n。

以下若干行每行四个正整数 x1,y1,x2,y2 表示第 x1 行第 y1 列的点和第 x2 行第 y2 列的点已经有连线。

输入保证|x1−x2|+|y1−y2|=1

输出格式

输出使得连通所有点还需要的最小花费。

数据范围

1≤m,n≤1000
0≤已经存在的连线数≤10000

输入样例：

2 2
1 1 2 1

输出样例：

3

  while(~scanf("%d %d %d %d",&x1,&y1,&x2,&y2))

如果scanf没有读入返回值-1，（~）这个符号就是二进制取反操作，-1取反后就变成0就退出while循环了

将二维坐标转化为一维坐标

比如（n=4,m=2)

1 2

3 4 

5 6

7 8

1 的二维坐标（1，1）----> 一维坐标 1

4 的二维坐标（2，2）----->一维坐标  4

故一维坐标转化为二维坐标 （x-1)*m+y 

先将给出的数连接好

在弄纵向的最后弄横向的

#include
using namespace std;
const int N=1010;
int f[N*N],ans;
int p[N*N];
int n,m;
//坐标初始化
void unit()
{
    for(int i=1;i<=n*m;i++) p[i]=i; 
}
//寻找祖先
int find(int x)
{
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}
int main()
{
    cin>>n>>m;
    unit();
    int x1,y1,x2,y2;
    while(~(scanf("%d%d%d%d",&x1,&y1,&x2,&y2)))
    {
        int a=(x1-1)*m+y1,b=(x2-1)*m+y2;
        int aa=find(a),bb=find(b);
        p[aa]=bb;
    }
    for(int j=1;j<=m;j++)//竖向合并一遍
    {
        for(int i=1;i