【脚踢数据结构】常见树总结(图码结和版)
- (꒪ꇴ꒪ ),Hello我是祐言QAQ
- 我的博客主页:C/C++语言,Linux基础,ARM开发板,软件配置等领域博主
- 快上,一起学习,让我们成为一个强大的攻城狮!
- 送给自己和读者的一句鸡汤:集中起来的意志可以击穿顽石!
- 作者水平很有限,如果发现错误,可在评论区指正,感谢
树(Tree)是一种常用的数据结构,用于表示层次结构的数据关系。它由一组节点(Nodes)以及连接这些节点的边(Edges)组成。树的一个重要特征是一个节点可以有零个或多个子节点,但每个节点只有一个父节点(除了根节点),从而形成一种层次化的结构。
一、树的基本概念
1.节点(Node):树的基本构建单元。每个节点可以包含一个数据元素,以及指向其他节点的链接(边)。树中的每个节点除了根节点外,都有且只有一个父节点,但可以有零个或多个子节点。
2.根节点(Root):树的顶层节点,它是整个树的起始点,没有父节点。
子节点(Children):一个节点的直接下层节点称为它的子节点。一个节点可以有零个、一个或多个子节点。
3.父节点(Parent):一个节点的直接上层节点称为它的父节点。
4.叶节点(Leaf):没有子节点的节点称为叶节点。叶节点位于树的末端,它们没有后继节点。
5.高度(深度):树的高度是指从根节点到树中任意节点的最长路径上的边数。叶节点的高度为0,树的高度取决于最深的路径即树中所有节点层次的最大值。
6.父子关系:树中节点之间的连接形成了父子关系。每个节点都有一个唯一的父节点,除了根节点。
7.子树(Subtree):对于一个节点,它的子树是由该节点及其所有后代节点组成的一棵子树。
8.节点的度(Degree):节点的度是指该节点拥有的子节点数量。二叉树的度为2,二叉搜索树的度可以是2或0/2。
9.树的类型:树有许多变种,包括二叉树、二叉搜索树、平衡树、红黑树等。不同类型的树在节点连接和数据存储方面具有不同的特点和规则。
二、树的特点
-
每棵树仅包含一个根节点,作为树的起始点。根节点是整个树的顶层节点,没有父节点与之关联。
-
树中的每个节点可以拥有多个孩子节点,但是不存在某个节点有多个父亲节点。每个节点只有一个父节点,形成了清晰的父子关系。
-
树中的叶子节点是没有子节点的节点,叶子节点的度为 0。叶子节点位于树的末端,没有后继节点,承载了终端数据。
-
树中所有节点的度(子节点数量)之和加上1等于树的总节点数。这一特点确保了每个节点的连接都被计算在内,形成了树的整体结构。
三、二叉树(Binary Tree)
一棵所有节点的度都不超过2的有序树被称为二叉树。在二叉树中,每个节点最多有两个孩子,分别称为左孩子和右孩子。即使节点只有一个孩子,仍然要区分左右孩子的位置。
1.完全二叉树
完全二叉树是指除最后一层外,其他所有层都是满的,并且最后一层的节点从左到右依次排列。换句话说,最后一层可以不满,但填充节点要从左至右进行。
2.满二叉树
满二叉树是一种特殊的完全二叉树,它的每一层(包括最后一层)都被节点填满,即每个节点的度都为2。
3.二叉树的特点
(1)如果一棵二叉树的深度为 k,那么该二叉树最多包含 2^k−1 个节点,最少包含 k 个节点。这是因为在深度为 k 的二叉树中,每一层的节点数最多为 2^(k−1),而总节点数是各层节点数的累加,所以最多有 2^k−1 个节点,最少情况是当树是一条链式结构时,只有一个路径上的 k 个节点。
(2)如果一棵完全二叉树的深度为 k,那么该二叉树最多包含 2^k−1 个节点,最少包含 2^(k−1)个节点。完全二叉树的特点是除了最后一层外,其它层都是满的,并且最后一层的节点依次从左至右排列。因此,完全二叉树的节点数取决于最后一层的节点数。
学完上述这些内容就来试试这七个小练习吧,答案在评论区:
(1)一个深度为h的二叉树最多有 个结点,最少有 个结点。
(2)一棵具有 257个结点的完全二叉树,它的深度为 。
(3)不相交的树的聚集称之为 。
(4)深度为k的完全二叉树至少有 个结点。至多有 个结点,
(5)高度为k,且有 个结点的二叉树称为满二叉树。
(6)高度为6的完全二叉树至少有 个结点。
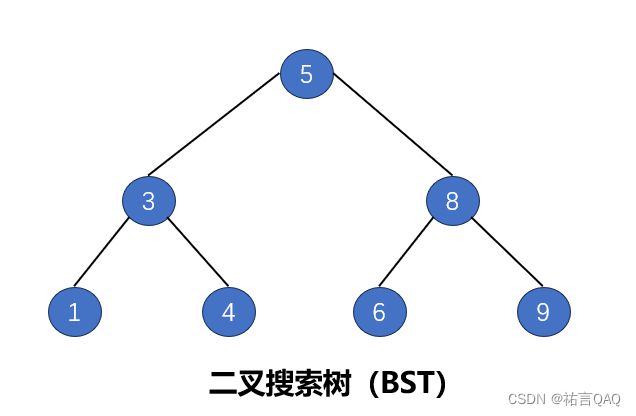
四、二叉搜索树(BST)
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,它具有以下特点和性质,使得在其中进行查找、插入和删除等操作变得高效:
1.节点结构:每个节点包含一个数据元素以及指向左子树和右子树的链接。
2. 左子树性质:对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值。
3. 右子树性质:对于树中的每个节点,其右子树中的所有节点的值都大于该节点的值。
4.递归定义:BST的定义是递归的,即每个子树也是BST。
五、树的遍历
树的遍历是指按照一定的顺序访问树中的所有节点,以便获取节点的信息或执行某些操作。常用的树的遍历方式包括先序遍历、中序遍历、后序遍历和按层遍历。下面我们以上图BST中的数据依次来演示并学习树的遍历。
1.先序遍历:“根-左-右”
先序遍历从根节点开始,首先访问根节点,然后按照先左后右的顺序递归遍历左子树和右子树。先序遍历的顺序是从上到下,从左到右的方式。
遍历结果:5 3 1 4 8 6 9。
2.中序遍历:“左-根-右”
中序遍历从根节点开始,先递归遍历左子树,然后访问根节点,最后再递归遍历右子树。中序遍历的顺序是从左到右,节点值从小到大的方式。在二叉搜索树中,中序遍历能够按升序输出节点值。
遍历结果:1 3 4 5 6 8 9。
3.后序遍历:“左-右-根”
后序遍历从根节点开始,先递归遍历左子树,然后递归遍历右子树,最后访问根节点。后序遍历的顺序是从下到上,从左到右的方式。
遍历结果:1 4 3 6 9 8 5。
4.按层遍历
从根节点开始,逐层地从左到右访问树的节点。
按层遍历使用队列来实现,首先将根节点入队,然后循环中,依次出队当前层的节点,将它们的子节点入队,以此类推,直到队列为空。这样能够按照从上往下,从左往右的顺序遍历整个树。
遍历结果:5 3 8 1 4 6 9。
相信看完上边的讲解,你一定跃跃欲试想告诉我你已经学会了树的遍历,那么就让题目来检验一下吧!(答案评论区见o)
(1)若某二叉树的前序遍历访问顺序是abdgcefh,中序遍历访问顺序是dgbaechf,则其按层遍历的结点访问顺序是?
(2)某二叉树的中序遍历结果为:ACBDFGEHI,先序遍历结果:EDCABFGHI,后序遍历结果是?
六、二叉搜索树的实现
二叉树的逻辑结构是非线性的,这意味着树中的节点之间存在一对多的关系,即每个节点可以有多个子节点,但只有一个父节点(除了根节点没有父节点)。
1.节点设计
typedef int Datatype;
//二叉搜索树节点结构体
typedef struct Node
{
Datatype data;//数据域
struct Node *lchild;左孩子的地址存放
struct Node *rchild;//右孩子的地址存放
}BT_node, *B_tree;2.初始化
//初始化
B_tree init_tree(void)
{
return NULL;//空的二叉搜索树,就是初始化一个根节点为NULL的一个节点
}3.新建节点
//创建新节点
B_tree create_node(Datatype data)
{
//为新节点申请空间
B_tree new = malloc(sizeof(BT_node));
if (new != NULL)
{
//节点初始化
new->data = data;
new->lchild = NULL;
new->rchild = NULL;
}
return new;
}4.插入节点
//插入节点:返回插入操作过后的根节点指针
//将new插入到以root为根节点的树中,返回插入过后的树的根节点
B_tree insert_node(B_tree root, B_tree new)
{
if (new == NULL)
{
return root;
}
//如果原来二叉搜索树是空的,
//那么第一次插入的节点就是根节点
if(is_empty(root))
{
return new;
}
//原本有节点的情况
else
{
//(1)新节点比root小,将new插入到root的左子树中
if (new->data < root->data)
{
root->lchild = insert_node(root->lchild, new);
}
//(2)新节点比root大,将new插入到root的右子树中
else if (new->data > root->data)
{
root->rchild = insert_node(root->rchild, new);
}
//(3)新节点与root相等,插入失败
else
{
printf("该节点存在,插入失败\n");
}
}
return root;
}5.查找节点
//查找节点
B_tree find_node(B_tree root, Datatype data)
{
if (is_empty(root))
{
return NULL;
}
else
{
// (1)待查数据小于根节点数据,从左子树中查找
if (data < root->data)
{
return find_node(root->lchild, data);
}
// (2)待查数据大于根节点数据,从右子树中查找
else if (data > root->data)
{
return find_node(root->rchild, data);
}
// (3)待查数据等于根节点数据
else
{
return root;
}
}
}6.删除节点
//删除节点
B_tree delete_node(B_tree root, Datatype data)
{
if (is_empty(root))
{
return root;
}
else
{
//待删数据比根节点数据小,在根节点的左子树中删除
if (data < root->data)
{
root->lchild = delete_node(root->lchild, data);
}
//待删数据比根节点数据大,在根节点的右子树中删除
else if (data > root->data)
{
root->rchild = delete_node(root->rchild, data);
}
//待删数据与根节点数据相等,那么根节点就是待删节点
else
{
//当待删节点有左子树,用左子树中最大节点接替待删节点
if (root->lchild != NULL)
{
//找左子树最大节点:不断往右边找
B_tree tmp = NULL;
for (tmp=root->lchild; tmp->rchild!=NULL; tmp=tmp->rchild);
root->data = tmp->data;//接替
//然后在左子树中删掉用来接替的节点
root->lchild = delete_node(root->lchild, tmp->data);
}
//当待删节点只有右子树,用右子树中最小节点接替待删节点
else if (root->rchild != NULL)
{
//找右子树最小节点:不断往左边找
B_tree tmp = NULL;
for (tmp=root->rchild; tmp->lchild!=NULL; tmp=tmp->lchild);
root->data = tmp->data;
//然后在右子树中删掉用来接替的节点
root->rchild = delete_node(root->rchild, tmp->data);
}
//当待删节点是目前子树的根节点,直接删除
else
{
free(root);
root = NULL;
}
}
}
return root;
}7.遍历
//(1)先序遍历 根节点-左子树-右子树
void pre_travel(B_tree root)
{
if (is_empty(root))
{
return;
}
printf("%d ", root->data);
pre_travel(root->lchild);
pre_travel(root->rchild);
}
//(2)中序遍历 左子树-根节点-右子树
void mid_travel(B_tree root)
{
if (is_empty(root))
{
return;
}
mid_travel(root->lchild);
printf("%d ", root->data);
mid_travel(root->rchild);
}
//(3)后序遍历 左子树-右子树-根节点
void post_travel(B_tree root)
{
if (is_empty(root))
{
return;
}
post_travel(root->lchild);
post_travel(root->rchild);
printf("%d ", root->data);
}
//(4)按层遍历
void level_travel(B_tree root)
{
if (root == NULL)
{
return;
}
//创建一个空队列
Lq q = init_queue();
//将根节点数据入队
in_queue(q, creat_queue_node(root->data));
Link get_queue_node;//获取出队元素的地址
while(1)
{
//出队队首(如果队列为空,遍历结束,跳出循环)
if (!out_queue(q, &get_queue_node))
{
break;
}
//出队的时候打印这个元素
printf("%d ", get_queue_node->data);
//出队数据对应的树节点的左右孩子入队
B_tree tree_node = find_node(root, get_queue_node->data);
if (tree_node->lchild != NULL)
{
in_queue(q, creat_queue_node(tree_node->lchild->data));
}
if(tree_node->rchild != NULL)
{
in_queue(q, creat_queue_node(tree_node->rchild->data));
}
}
}
七、自平衡树 AVL
AVL树(Adelson-Velsky and Landis tree)是一种自平衡二叉搜索树,它在插入和删除操作后会自动调整节点的位置,以保持树的平衡性。平衡性指的是树的左右子树高度差不超过1,从而保证树的查找、插入和删除操作的时间复杂度都能保持在较低的水平。
此外AVL树的平衡性是通过节点的高度差(称为平衡因子)来维护的。平衡因子是左子树高度减去右子树高度的值。在AVL树中,每个节点的平衡因子必须在-1、0和1之间。
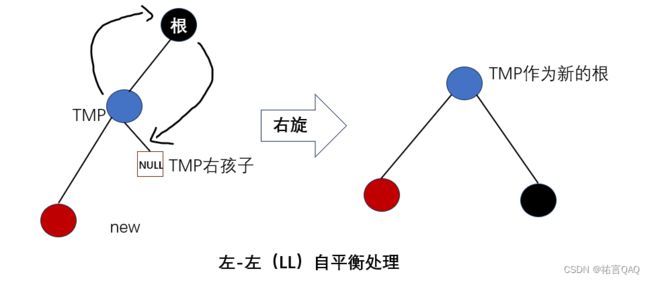
1.左-左(LL)不平衡
当一个节点的左子树的左子树高度比右子树高度大2或更多时,就会发生LL不平衡。这可以通过右旋操作来解决。
2.左-右(LR)不平衡
当一个节点的左子树的右子树高度比左子树高度大2或更多时,就会发生LR不平衡。这可以通过先对左子树进行左旋,然后对整个树进行右旋来解决。
3.右-右(RR)不平衡
当一个节点的右子树的右子树高度比左子树高度大2或更多时,就会发生RR不平衡。这可以通过左旋操作来解决。
4.右-左(RL)不平衡
当一个节点的右子树的左子树高度比右子树高度大2或更多时,就会发生RL不平衡。这可以通过先对右子树进行右旋,然后对整个树进行左旋来解决。
八、AVL代码实现
1.数据结构定义
定义一个结构 Avl_node 来表示AVL树的节点,包括节点的数据、高度、左孩子和右孩子。
typedef int Datatype;
typedef struct Avl_Node
{
Datatype data; //数据
int height; //高度
struct Avl_Node *lchild; //左孩子
struct Avl_Node *rchild; //右孩子
}Avl_node;2.初始化和创建节点
通过 init_avl 函数初始化一棵空的AVL树, create_avl_node 函数创建一个新的AVL节点。
//初始化
Avl_node *init_avl()
{
return NULL;
}
//创建节点
Avl_node *create_avl_node(Datatype data)
{
Avl_node *new = malloc(sizeof(Avl_node));
if (new != NULL)
{
new->data = data;
new->height = 1;
new->lchild = NULL;
new->rchild = NULL;
}
return new;
}3.获取孩子的高度并更新
get_height 函数用于获取节点的高度,max 函数用于更新两个整数中的较大值。
//获取孩子的高度
int get_height(Avl_node *root)
{
if (root == NULL)
{
return 0;
}
return root->height;
}
//高度更新
int max(int h1, int h2)
{
return h1>h2?h1:h2;
}4.左旋和右旋操作
avl_left 函数实现左旋操作,avl_right 函数实现右旋操作,通过这些操作可以调整树的结构以维持平衡。
//左旋
Avl_node *avl_left(Avl_node *root)
{
Avl_node *tmp = root->rchild;
root->rchild = tmp->lchild;
tmp->lchild = root;
root->height = max(get_height(root->lchild), get_height(root->rchild))+1;
tmp->height = max(get_height(tmp->lchild), get_height(tmp->rchild))+1;
return tmp;
}
//右旋
Avl_node *avl_right(Avl_node *root)
{
Avl_node *tmp = root->lchild;
root->lchild = tmp->rchild;
tmp->rchild = root;
root->height = max(get_height(root->lchild), get_height(root->rchild))+1;
tmp->height = max(get_height(tmp->lchild), get_height(tmp->rchild))+1;
return tmp;
}5.自平衡处理
avl_opt 函数用于在插入和删除节点后进行自平衡处理,根据节点的高度差进行旋转操作来维持树的平衡性。
//自平衡处理
Avl_node *avl_opt(Avl_node *root)
{
//(1)左边不平衡
//root的左子树高度-右子树高度 > 1
if (get_height(root->lchild)-get_height(root->rchild)>1)
{
// ①左-左不平衡:(root->lchild->lchild)的高度 >= (root->lchild->rchild)的高度
if (get_height(root->lchild->lchild) >= get_height(root->lchild->rchild))
{
//右旋
root = avl_right(root);
}
// ②左-右不平衡:(root->lchild->lchild)的高度 < (root->lchild->rchild)的高度
else if (get_height(root->lchild->lchild) < get_height(root->lchild->rchild))
{
//左旋
root->lchild = avl_left(root->lchild);
//右旋
root = avl_right(root);
}
}
//(2)右边不平衡 root的右子树高度-左子树高度 > 1
else if (get_height(root->rchild)-get_height(root->lchild)>1)
{
// ③右-右不平衡:(root->rchild->rchild)的高度 >= (root->rchild->lchild)的高度
if (get_height(root->rchild->rchild) >= get_height(root->rchild->lchild))
{
//左旋
root = avl_left(root);
}
// ④右-左不平衡:(root->rchild->rchild)的高度 < (root->rchild->lchild)的高度
else if (get_height(root->rchild->rchild) < get_height(root->rchild->lchild))
{
//右旋
root->rchild = avl_right(root->rchild);
//左旋
root = avl_left(root);
}
}
//(3)平衡
else
{}
return root;
}6.插入节点
insert_avl_node 函数用于将新节点插入AVL树中,并在插入后执行自平衡操作。
//插入节点
Avl_node *insert_avl_node(Avl_node *root, Avl_node *new)
{
if (new == NULL)
{
return root;
}
//如果是第一次插入,没有任何节点
if (root == NULL)
{
return new;
}
else
{
//新节点放在根的左边,还是右边
if (new->data < root->data)//新节点小于根节点,放左边
{
//根节点的左边还有左孩子的情况
root->lchild = insert_avl_node(root->lchild, new);
}
else if (new->data > root->data)//新节点大于根节点,放右边
{
//根节点的右边还有右孩子的情况
root->rchild = insert_avl_node(root->rchild, new);
}
else
{
printf("二叉树里面已经有这个节点\n");
}
}
//自平衡处理
root = avl_opt(root);
//高度更新
root->height = max(get_height(root->lchild), get_height(root->rchild))+1;
return root;
}7.遍历操作
display_prec 和 display_mid 函数分别实现了AVL树的先序遍历和中序遍历。
//先序
void display_prec(Avl_node *root)
{
if (root == NULL)
{
return ;
}
printf("%d ", root->data);
display_prec(root->lchild);
display_prec(root->rchild);
}
//中序
void display_mid(Avl_node *root)
{
if (root == NULL)
{
return ;
}
display_mid(root->lchild);
printf("%d ", root->data);
display_mid(root->rchild);
}8.删除节点
dele_node 函数用于删除指定数据的节点,并根据情况进行自平衡操作。
//删除节点
Avl_node *dele_node(Avl_node *root, Datatype data)
{
if (root == NULL)
{
return root;
}
else
{
//如果删除节点比根节点小,去左子树中找要删除的节点
if (root->data > data)
{
root->lchild = dele_node(root->lchild, data);
}
//如果删除节点比根节点大,去右子树中找要删除的节点
else if (root->data < data)
{
root->rchild = dele_node(root->rchild, data);
}
//删除节点等于根节点
else
{
//1、当待删除的节点有左子树,用左子树中最大的值来替换掉删除的节点
//保证二叉树满足BST的特性
if (root->lchild!=NULL)
{
//找左子树中最大的节点,不断往右找
Avl_node *tmp = NULL;
for (tmp = root->lchild; tmp->rchild!=NULL; tmp = tmp->rchild);
//最大的节点接替要删除的节点
root->data = tmp->data;
//然后在左子树中删掉用来接替的节点
root->lchild = dele_node(root->lchild, tmp->data);
}
//2、当待删除的节点没有左子树,只有右子树,用右子树中最小的值来替换掉删除的节点
else if (root->rchild!=NULL)
{
//找右子树中最小的节点,不断往左找
Avl_node *tmp = NULL;
for(tmp=root->rchild; tmp->lchild!=NULL; tmp = tmp->lchild);
//最小的节点接替要删除的节点
root->data = tmp->data;
//然后在右子树中删掉用来接替的节点
root->rchild = dele_node(root->rchild, tmp->data);
}
//3、待删除节点,即没有左子树,也没有右子树,就是一个叶子节点,直接删除
else
{
free(root);
root = NULL;
}
}
}
//如果删除的节点返回的root为空
if (root == NULL)
{
return root;
}
//自平衡处理
root = avl_opt(root);
//高度更新
root->height = max(get_height(root->lchild), get_height(root->rchild))+1;
return root;
}9.例程
循环读取输入的正整数和负整数,正整数表示插入节点,负整数表示删除节点,0 表示输出遍历结果:
int main(int argc, char const *argv[])
{
//初始化一棵空的avl树
Avl_node *root = init_avl();
//新建节点并插入树结构
int num;
while(1)
{
scanf("%d", &num);
if (num > 0)
{
//新建节点
Avl_node * new = create_avl_node(num);
//插入节点
root = insert_avl_node(root, new);
}
else if (num < 0)
{
root = dele_node(root, -num);
}
else
{
printf("先序遍历:");
display_prec(root);
printf("\n中序遍历:");
display_mid(root);
printf("\n");
}
}
return 0;
}九、哈夫曼树
哈夫曼树(Huffman Tree)是一种用于编码和压缩数据的树形数据结构。它是一种特殊的二叉树,用于将出现频率较高的字符(或符号)用较短的二进制编码表示,从而实现数据的高效存储和传输。
也可以说当有n个叶子节点,每个节点都有各自的权,试图创建一个带权路径长度最小的树,这棵树就是最优二叉树就叫哈夫曼树。
1.基本概念
在下面的例子中,我们将解释路径、路径长度、结点的权、结点的带权路径长度以及树的带权路径长度(WPL)。
(1)路径: 路径是从一个节点到另一个节点的通路。例如,从根节点到节点 5 的路径可以是:15 -> 8 -> 5。
(2)路径长度: 在一条路径中,每经过一个节点,路径长度都要加 1。例如,从根节点到节点 5 的路径长度为 2(15 -> 8 -> 5)。
(3)结点的权: 每个节点都有一个权重值。在这个例子中,节点 15 的权重为 15,节点 8 的权重为 8,以此类推。
(4)结点的带权路径长度: 结点的带权路径长度是指从根节点到该节点之间的路径长度与该节点的权重的乘积。例如,节点 5 的带权路径长度为 2(路径长度) * 5(权重) = 10。
(5)树的带权路径长度(WPL): 树的带权路径长度是指树中所有叶子节点的带权路径长度之和。在这个例子中,树的 WPL 为:(2 * 3) + (2 * 5) + (3 * 7) + (3 * 8) + (3 * 12) + (1 * 15) = 84。
2.哈夫曼编码
哈夫曼编码是一种用于将字符或符号编码为二进制的压缩编码方法,旨在通过分配较短的编码给出现频率较高的字符,以实现数据的高效压缩和传输。这种编码方式以哈夫曼树为基础,根据字符出现的频率构建一个最优的二叉树,然后通过从根节点到叶子节点的路径来表示字符的编码。
下面是哈夫曼编码的基本步骤:
(1)统计字符频率: 对要编码的数据进行字符频率的统计,通常使用频率表来记录每个字符出现的次数。
(2)构建哈夫曼树: 根据字符频率构建哈夫曼树,即从频率最低的叶子节点开始,每次选择两个频率最低的节点作为子节点,将它们的频率相加作为父节点的频率,重复这个过程直到只剩下一个根节点。
(3)分配编码: 在哈夫曼树中,沿着左子树路径走的编码为 0,沿着右子树路径走的编码为 1。从根节点开始,沿着路径到达叶子节点,记录路径上的编码,即可得到字符的哈夫曼编码。
(4)生成编码表: 将字符和对应的哈夫曼编码建立映射关系,构建编码表,以便后续编码和解码使用。
下面就让我们动手来画一个哈夫曼树并构建编码表:
这是我们统计的字符频率,下面就从频率最小的两个字符开始,从下往上绘制二叉树,每绘制一个二叉树就要把其和求出来给到根,再从剩余的多有字符和根中调出次小的两个值,再次形成一个二叉树,以此类推直到完成所有。然后再对其分配编码,沿着左子树路径走的编码为 0,沿着右子树路径走的编码为 1。
3.哈弗曼树的应用领域
哈夫曼树的主要思想是将频率较高的字符分配较短的编码,而频率较低的字符分配较长的编码,以便在编码和解码过程中减少数据的长度。这种编码方式称为哈夫曼编码,它是一种前缀编码,即任何一个字符的编码不是另一个字符编码的前缀,从而确保解码时不会产生歧义。
因此哈夫曼树在信息传输、数据存储和压缩领域具有重要的应用,常用于压缩文件、图像、音频等数据,以便有效地减少存储空间和传输带宽。由于哈夫曼编码是无损压缩,解码后可以完全还原原始数据,因此被广泛应用于通信和存储领域。
为了方便大家理解与掌握,那么再出一道题(答案评论区)。
4. 数组方式构建哈夫曼树(C语言)
#include
#include
#define MAX_TREE_HT 100 // 定义最大树高
struct MinHeapNode { // 定义最小堆节点的结构体
char data; // 节点数据
unsigned freq; // 节点频率
struct MinHeapNode *left, *right; // 左右子节点指针
};
struct MinHeap { // 定义最小堆结构体,用于构建哈夫曼树
unsigned size; // 堆的大小
unsigned capacity; // 堆的容量
struct MinHeapNode** array; // 存储堆节点指针的数组
};
struct MinHeapNode* newNode(char data, unsigned freq) { // 创建新的最小堆节点
struct MinHeapNode* temp = (struct MinHeapNode*)malloc(sizeof(struct MinHeapNode)); // 分配节点内存
temp->left = temp->right = NULL; // 初始化左右子节点指针为空
temp->data = data; // 设置节点数据
temp->freq = freq; // 设置节点频率
return temp; // 返回新创建的节点
}
struct MinHeap* createMinHeap(unsigned capacity) { // 创建最小堆
struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap)); // 分配堆内存
minHeap->size = 0; // 初始化堆大小为0
minHeap->capacity = capacity; // 设置堆容量
minHeap->array = (struct MinHeapNode**)malloc(minHeap->capacity * sizeof(struct MinHeapNode*)); // 分配存储节点指针的数组内存
return minHeap; // 返回新创建的堆
}
void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b) { // 交换最小堆节点
struct MinHeapNode* t = *a; // 临时变量保存节点a的值
*a = *b; // 将节点b的值赋给节点a
*b = t; // 将临时变量中保存的节点a的值赋给节点b
}
void minHeapify(struct MinHeap* minHeap, int idx) { // 对最小堆进行维护,确保满足最小堆性质
int smallest = idx; // 初始化最小元素索引为传入的索引
int left = 2 * idx + 1; // 左子节点索引
int right = 2 * idx + 2; // 右子节点索引
if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[smallest]->freq)
smallest = left; // 如果左子节点的频率小于最小元素的频率,则更新最小元素索引
if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[smallest]->freq)
smallest = right; // 如果右子节点的频率小于最小元素的频率,则更新最小元素索引
if (smallest != idx) { // 如果最小元素索引不等于传入的索引
swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]); // 交换最小元素和传入索引对应的元素
minHeapify(minHeap, smallest); // 递归调整子堆
}
}
int isSizeOne(struct MinHeap* minHeap) { // 判断堆的大小是否为1
return (minHeap->size == 1); // 如果堆的大小为1,则返回1,否则返回0
}
struct MinHeapNode* extractMin(struct MinHeap* minHeap) { // 从堆中取出频率最小的节点
struct MinHeapNode* temp = minHeap->array[0]; // 获取堆的根节点
minHeap->array[0] = minHeap->array[minHeap->size - 1]; // 将堆的最后一个节点移动到根节点
--minHeap->size; // 减小堆的大小
minHeapify(minHeap, 0); // 调整堆,确保满足最小堆性质
return temp; // 返回取出的节点
}
void insertMinHeap(struct MinHeap* minHeap, struct MinHeapNode* minHeapNode) { // 向堆中插入节点
++minHeap->size; // 增加堆的大小
int i = minHeap->size - 1; // 获取插入节点的索引
while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) { // 如果插入节点的频率小于其父节点的频率
minHeap->array[i] = minHeap->array[(i - 1) / 2]; // 将父节点向下移动
i = (i - 1) / 2; // 更新索引为父节点的索引
}
minHeap->array[i] = minHeapNode; // 将插入节点放入合适的位置
}
void buildMinHeap(struct MinHeap* minHeap) { // 构建最小堆
int n = minHeap->size - 1; // 获取堆的大小
int i;
for (i = (n - 1) / 2; i >= 0; --i) // 从堆的非叶子节点开始,逐步调整堆以满足最小堆性质
minHeapify(minHeap, i);
}
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) { // 创建并构建最小堆
struct MinHeap* minHeap = createMinHeap(size); // 创建最小堆
for (int i = 0; i < size; ++i)
minHeap->array[i] = newNode(data[i], freq[i]); // 将数据和频率转化为最小堆节点插入堆中
minHeap->size = size; // 设置堆的大小为传入的大小
buildMinHeap(minHeap); // 构建最小堆
return minHeap; // 返回构建好的最小堆
}
十、红黑树
1.基本概念和特点
红黑树(Red-Black Tree)是一种自平衡二叉搜索树, 红黑树满足平衡的要求为:左右子树高度差不能超过一倍;一般称其为相对平衡树,而叫AVl为绝对平衡树。它具有以下特点:
(1)树中的节点都是有颜色的,要么红色要么黑色;
(2)树的根节点颜色是黑色;
(3)空节点的颜色算作黑色;
(4)不能有连续的红色节点(任意一对父子节点不可能都是红色节点),但黑色节点可任意连续;
(5)从任意一个节点开始到叶子节点的路径包含的黑色节点个数是相等的。
2.红黑树节点的插入
(1)创建新节点,着色为红色;
(2)如果树为空,将该节点颜色设置为黑色,作为树的根节点;
(3)如果树不为空,用BST的方式插入新节点;
(4)判断树是否平衡,做平衡处理。
3.红黑树不平衡处理
一个基本的红黑树包含,根节点G(祖父)、P节点(父)、U节点(叔)以及新节点(N),下面我们就N的不同来讨论当红黑树不平衡是该如何使之平衡。
(1)当父节点P的颜色为黑色,直接插入不影响平衡性
(2)当父节点P的颜色为红色时我们就要分多组来讨论了,首先是:
①叔叔节点U的颜色也是红色
I.父亲节点为祖父节点的左孩子
·新节点是左孩子
a.直接将U和P颜色改为黑色,G的颜色该为红色
b.将祖父节点作为新节点取讨论平衡性
·新节点是右孩子
a.直接将U和P颜色改为黑色,G的颜色改为红色
b.将祖父节点作为新节点取讨论平衡性
II.父亲节点为祖父节点的右孩子
这种情况与上述的父亲节点为祖父节点的左孩子基本一致,只是更换了方向,结和上两幅图很容易推理得出,这里就不赘述了。
②叔叔节点U的颜色为黑色
I.父亲节点为祖父节点的左孩子
·新节点是左孩子
a.将P和G变颜色
b.将现在的P和G进行右旋
·新节点是右孩子
a.将P和N这组关系进行左旋
b.将变化过后的新的P和G变颜色
c.将现在的P和G进行右旋
II.父亲节点为祖父节点的右孩子
·新节点是左孩子
a.将P和N进行右旋
b.将变化后的P和G变颜色
c.将现在的P和G进行左旋
·新节点是右孩子
a.将变化后的P和G变颜色
b.将现在的P和G进行左旋
对于红黑树呢代码也较为复杂,因此我们只需掌握基本逻辑即可,代码可在网上很容易搜到,有兴趣的同学自己找一下,也可以来找我私信。
更多C语言、Linux系统、ARM板实战和数据结构相关文章,关注专栏:
手撕C语言
玩转linux
脚踢数据结构
6818(ARM)开发板实战
写在最后
- 今天的分享就到这啦~
- 觉得博主写的还不错的烦劳
一键三连喔~ - 感谢关注