强化学习 PPO算法和代码

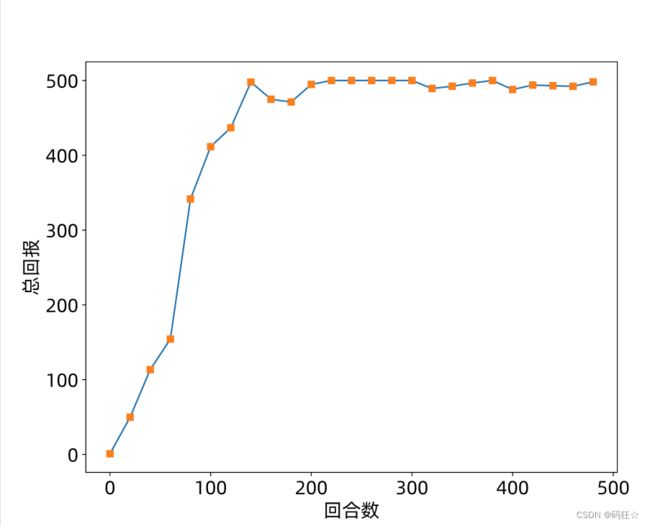
PPO 效果

前提

τ ~ p(τ) 是轨迹分布
t∈[0,T-1] 是一条轨迹的步骤数
策略 π 是动作 a 的概率分布

State-Action Value Function 简称 V(st) 函数

$$V^{\pi }(s_t)=E_{\tau \sim p(\tau )}[R({\tau }_{t:T})|{\tau }_{s_t}=s_t]$$
$$V^{\pi }(s_t)=E_{\tau \sim p(\tau )}[r(s_t)+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+...]$$
V(st)函数的贝尔曼方程：
$$V^{\pi }(s_t)=E_{\tau \sim p(\tau )}[r(s_t)+\gamma V^{\pi }(s_{t+1})]$$

State-Action Value Function 简称 Q(st,at) 函数

它定义为环境在状态st智能体在策略π控制执行动作at的条件下， 能获得的期望回报值：
$$Q^{\pi }(s_t,a_t)=E_{\tau \sim p(\tau )}[R({\tau }_{t:T})|{\tau }_{a_t}=a_t,{\tau }_{s_t}=s_t]$$
$$Q^{\pi }(s_t,a_t)=E_{\tau \sim p(\tau )}[r(s_t,a_t)+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+...]$$
$$Q^{\pi }(s_t,a_t)=E_{\tau \sim p(\tau )}[r(s_t,a_t)+\gamma V^{\pi }(s_{t+1})]$$
这里有两个随机变量 st 和 at ,其中由于, 已确定， (, )也是确定值
Q 函数与 V 函数直接存在如下关系,:
$$V^{\pi }(s_t)=E_{a_t\sim \pi (a_t|s_t)}[Q^{\pi }(s_t,a_t)]$$
当采样自(|)策略时， Q(st,at) 对动作 a 求期望 与 V(st)相等
说明 V(st) 是策略(|)下执行动作 at 的平均回报

我们把(, )与()的差定义为优势值函数：

$$A^{\pi }(s,a)\underset{=}{△}{Q}^{\pi }(s,a)-V^{\pi }(s)$$
它表明在状态下采取动作比平均水平的优势程度： (, ) > 0时说明采取动作要优于平均水平；反之则劣于平均水平

字体找不到

ubuntu python findfont: Font family ‘Alibaba PuHuiTi 3.0’ not found.

shell 清除缓存：

rm ~/.cache/matplotlib -rf

到这里下载 阿里巴巴普惠体3.0 https://fonts.alibabagroup.com/
然后安装字体

PPO

其中 gym version = 0.26.2 https://github.com/openai/gym/releases/tag/0.26.2

import  matplotlib
from 	matplotlib import pyplot as plt
matplotlib.rcParams['font.size'] = 18
matplotlib.rcParams['figure.titlesize'] = 18
matplotlib.rcParams['figure.figsize'] = [9, 7]
matplotlib.rcParams['font.family'] = ['Alibaba PuHuiTi 3.0']
matplotlib.rcParams['axes.unicode_minus']=False

plt.figure()

import  gym,os
import  numpy as np
import  tensorflow as tf
from    tensorflow import keras
from    tensorflow.keras import layers,optimizers,losses
from    collections import namedtuple
# from    torch.utils.data import SubsetRandomSampler,BatchSampler

SEED_NUM = 2222
env = gym.make('CartPole-v0')  # 创建游戏环境
#env.seed(SEED_NUM )
tf.random.set_seed(SEED_NUM )
np.random.seed(SEED_NUM )
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
assert tf.__version__.startswith('2.')



gamma = 0.98 # 激励衰减因子
epsilon = 0.2 # PPO误差超参数0.8~1.2
batch_size = 32 # batch size


# 创建游戏环境
env = gym.make('CartPole-v1').unwrapped
Transition = namedtuple('Transition', ['state', 'action', 'a_log_prob', 'reward', 'next_state'])


class Actor(keras.Model):
    """ 策略网络 """
    def __init__(self):
        super(Actor, self).__init__()
        # 策略网络，也叫Actor网络，输出为概率分布pi(a|s)
        self.fc1 = layers.Dense(100, kernel_initializer='he_normal')
        self.fc2 = layers.Dense(2, kernel_initializer='he_normal')

    def call(self, inputs):
        x = tf.nn.relu(self.fc1(inputs))
        x = self.fc2(x)
        x = tf.nn.softmax(x, axis=1) # 转换成概率
        return x

class Critic(keras.Model):
    """ 奖励预测网络 """
    def __init__(self):
        super(Critic, self).__init__()
        # 偏置b的估值网络，也叫Critic网络，输出为v(s)
        self.fc1 = layers.Dense(100, kernel_initializer='he_normal')
        self.fc2 = layers.Dense(1, kernel_initializer='he_normal')

    def call(self, inputs):
        x = tf.nn.relu(self.fc1(inputs))
        x = self.fc2(x)
        return x




class PPO():
    # PPO算法主体
    def __init__(self):
        super(PPO, self).__init__()
        self.actor = Actor() # 创建Actor网络
        self.critic = Critic() # 创建Critic网络
        self.buffer = [] # 数据缓冲池
        self.actor_optimizer = optimizers.Adam(1e-3) # Actor优化器
        self.critic_optimizer = optimizers.Adam(3e-3) # Critic优化器

    def select_action(self, s):
        # 送入状态向量，获取策略: [4]
        s = tf.constant(s, dtype=tf.float32)
        # s: [4] => [1,4]
        s = tf.expand_dims(s, axis=0)
        # 获取策略分布: [1, 2]
        prob = self.actor(s)
        # 从类别分布中采样1个动作, shape: [1]
        a = tf.random.categorical(tf.math.log(prob), 1)[0]
        a = int(a)  # Tensor转数字
        return a, float(prob[0][a]) # 返回动作及其概率

    def get_value(self, s):
        # 送入状态向量，获取策略: [4]
        s = tf.constant(s, dtype=tf.float32)
        # s: [4] => [1,4]
        s = tf.expand_dims(s, axis=0)
        # 获取策略分布: [1, 2]
        v = self.critic(s)[0]
        return float(v) # 返回v(s)

    def store_transition(self, transition):
        # 存储采样数据
        self.buffer.append(transition)

    def optimize(self):
        # 优化网络主函数
        # 从缓存中取出样本数据，转换成Tensor
        state = tf.constant([t.state for t in self.buffer], dtype=tf.float32)
        action = tf.constant([t.action for t in self.buffer], dtype=tf.int32)
        action = tf.reshape(action,[-1,1])
        reward = [t.reward for t in self.buffer]
        old_action_log_prob = tf.constant([t.a_log_prob for t in self.buffer], dtype=tf.float32)
        old_action_log_prob = tf.reshape(old_action_log_prob, [-1,1])
        # 通过MC方法循环计算R(st)
        R = 0
        Rs = []
        for r in reward[::-1]: #逆序计算每一时刻t步骤的回报
            R = r + gamma * R
            Rs.insert(0, R)
        Rs = tf.constant(Rs, dtype=tf.float32)
        # 对缓冲池数据大致迭代10遍
        for _ in range(round(10*len(self.buffer)/batch_size)):
            # 随机从缓冲池采样batch_size大小样本
            index = np.random.choice(np.arange(len(self.buffer)), batch_size, replace=False)
            # 构建梯度跟踪环境
            with tf.GradientTape() as tape1, tf.GradientTape() as tape2:
                # 取出R(st)采样真实值，[b,1] ,shape=(batch_size,1)
                v_target = tf.expand_dims(tf.gather(Rs, index, axis=0), axis=1)
                # 计算v(s)预测值，也就是偏置b，我们后面会介绍为什么写成v,shape=(batch_size,1)
                v = self.critic(tf.gather(state, index, axis=0))
                delta = v_target - v # 计算优势值，采样真实值与预测值的误差,shape=(batch_size,1)
                advantage = tf.stop_gradient(delta) # 断开梯度连接 ,shape=(batch_size,1)

                # 由于TF的gather_nd与pytorch的gather功能不一样，需要构造
                # gather_nd需要的坐标参数，indices:[b, 2]
                # pi_a = pi.gather(1, a) # pytorch只需要一行即可实现
                
                a = tf.gather(action, index, axis=0) # 取出batch的动作at , shape=(batch_size,1)
                pi = self.actor(tf.gather(state, index, axis=0)) # batch的状态st预测动作a分布pi(a|st) shape=(batch_size,2)
                indices = tf.expand_dims(tf.range(a.shape[0]), axis=1) #shape=(batch_size,1)
                indices = tf.concat([indices, a], axis=1) #shape=(batch_size,2),第1列是索引indices，第2列是a,a∈[0,1]也相当于索引
                pi_a = tf.gather_nd(pi, indices)  # pi预测中按照indices索引取出动作的概率值pi(at|st), shape=(batch_size,)
                pi_a = tf.expand_dims(pi_a, axis=1) # shape=(batch_size,1)
                # 重要性采样 = 预测概率/采样真实概率
                ratio = (pi_a / tf.gather(old_action_log_prob, index, axis=0)) # shape=(batch_size,1)
                surr1 = ratio * advantage  # shape=(batch_size,1)
                surr2 = tf.clip_by_value(ratio, 1 - epsilon, 1 + epsilon) * advantage  # shape=(batch_size,1)
                # PPO误差函数
                policy_loss = -tf.reduce_mean(tf.minimum(surr1, surr2)) # shape=()
                # 对于偏置v来说，希望与MC估计的R(st)越接近越好
                value_loss = losses.MSE(v_target, v) # shape=(batch_size,)
            # 优化策略网络
            grads = tape1.gradient(policy_loss, self.actor.trainable_variables)
            self.actor_optimizer.apply_gradients(zip(grads, self.actor.trainable_variables))
            # 优化偏置值网络
            grads = tape2.gradient(value_loss, self.critic.trainable_variables)
            self.critic_optimizer.apply_gradients(zip(grads, self.critic.trainable_variables))

        self.buffer = []  # 清空已训练数据


def main():
    agent = PPO()
    returns = [] # 统计总回报
    total = 0 # 一段时间内平均回报
    for i_epoch in range(500): # 训练回合数
        state,info = env.reset(seed=SEED_NUM) # 复位环境
        for t in range(500): # 最多考虑500步
            # 通过最新策略与环境交互
            action, action_prob = agent.select_action(state)
            #next_state, reward, done, _ , _= env.step(action)
            next_state, reward, done, truncated, info = env.step(action)
            # 构建样本并存储 
            trans = Transition(state, action, action_prob, reward, next_state)
            agent.store_transition(trans)
            state = next_state # 刷新状态
            total += reward # 累积激励
            if done: # 合适的时间点训练网络
                if len(agent.buffer) >= batch_size:
                    agent.optimize() # 训练网络
                break

        if i_epoch % 20 == 0: # 每20个回合统计一次平均回报
            returns.append(total/20)
            total = 0
            print(i_epoch, returns[-1])

    print(np.array(returns))
    plt.figure()
    plt.plot(np.arange(len(returns))*20, np.array(returns))
    plt.plot(np.arange(len(returns))*20, np.array(returns), 's')
    plt.xlabel('回合数')
    plt.ylabel('总回报')
    plt.savefig('ppo-tf-cartpole.svg')


if __name__ == '__main__':
    main()
    print("end")