【C++】位图和布隆过滤器

前言

本来本篇是和前面的两篇连着的，但是没写到一块，位图和布隆过滤器都是基于哈希的思想的，如果对于哈希不熟悉的同学可以看看前两篇（重点看第一篇）：
【C++】模拟实现哈希（闭散列和开散列两种方式）

【C++】模拟实现unordered_map和unordered_set

正式开始

位图

先提个问题：现在有40亿个不重复的无符号整数，无序的，给你一个无符号整数，如何判断出该树是否在这40亿个数中？

各位有思路吗？

先算算40亿个无符号整数有多大吧，一个无符号整数4Byte，40亿个4Byte，也就是160亿Byte。看着不太方便，我们把它转成G来看。

一个G多少个Byte呢？1G = 1024MB = 1024 * 1024 KB = 1024 * 1024 * 1024 B，也就是 2³⁰ B。
那么1G大概就是10亿多B，我们就按照1G为10亿B来说的话，160亿B大概就是16G（实际比16G小一点）。16个G，内存中是绝对放不下的，所以就不要想着用set/unordered_set了。

那么该用啥呢？

就是马上要讲的位图。

位图讲解

其实我前面博客中讲Linux的时候已经提到过位图了，就在讲文件的那篇博客中，磁盘上的文件存储的时候就用到了位图。

那位图是干嘛的？
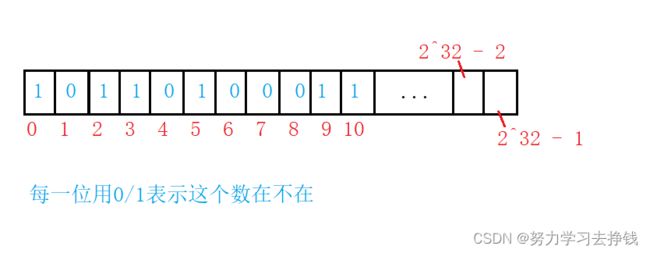
接着开始的问题，如果我们用一个bit位来表示一个数（0表示数不在，1表示数在），是否可行？
先来算算，用一个bit位表示一个数的话，总共40亿个数，那就是10多就是2³⁰，40亿就是2³²,那么就需要2³²个bit位。这是多大呢？ 一个Byte有8个bit位，也就是2³，那么2³²个bit位就是2²⁹个Byte，1G是2³⁰B，那么2²⁹个Byte就是0.5G，也就是512MB。

这样的话，内存完全是可以存下的。

那么如何记录某一个数呢？
也很简单，看图：

这就是位图。

前面哈希中讲了直接定址法 ==》不存在哈希冲突。
但主要讲了除留余数法 ==》存在哈希冲突

而这里的的位图用的是直接定制法，是不存在哈希冲突的，只要位图开得够大每个整数数都一定会有其固定的位置，因为整数是有范围的，0 ~ 42亿多，用2³²个bit位就能存放下所有的整数。

STL库中也是给了位图的，就叫做bitset，但是先不看STL库中的，下面我们就先模拟实现一下位图。

模拟实现位图

我们可以用顺序表来实现，顺序表中可以存储整形家族的元素，具体哪一种取决于你自己。

我这里直接用char了，char一个字节更方便一点，一个字节就是8bit位，存储2³²个bit的话，再除以四就是2²⁹个char。但我们这里实现的就先不给固定大小，万一数字个数不是这么多还可以改。

写到命名空间中，方便和库中的区分：

位图其实就只需要实现3个重要的接口，set、reset、test。
set是将数设置到位图中，也就是置一操作；reset就是将数从为图中去除，也就是置零操作；test就是检测某个数是否在位图当中。

但实现这三个接口之前，我们先要设置位图要开多大的空间。

我们可以给一个非类型模版参数：

N就是有多少个数。

假如说我们这里只需要开10个数，那么就要用10bit位来表示这十个数，如果存放的是char，一个char八个Byte，那么就需要开 10 / 8 + 1个char就够了。那如果开N个数，就需要 N/8 + 1就够了。可能有同学说，这样的话如果N是8的倍数，不就浪费了8个bit了吗？没关系，8个bit才多大，就一个char而已，浪费不了多少的。

那就要在构造函数中开空间：

然后再来写set，如果想要让一个数在位图的对应位置中设置为1，怎么搞呢？

看图：

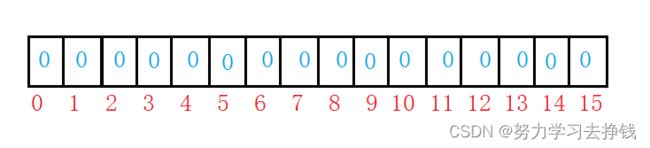
表大小为16，如果想让第12个位置变为1。

可以让12 / 8得到的就是12在第i个char中，再让12%8得到的就是12在某个char中的第j个位置。
然后我们搞一个1，让1左移j位，然后和_bits[i]相或，就能让对应数的位置置为1。

再说reset，反过来，让_bits[i] &= ~(1<

test更简单，&后的结果是否为0，为零就不存在，不为零就存在。

测试一下：

调试看看：

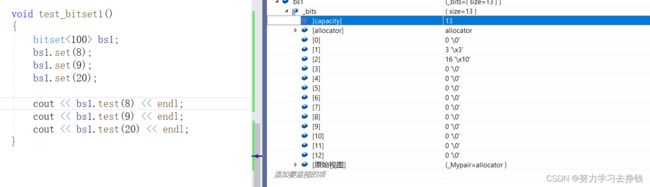
上面8算后的就是第二个char最低位，9是第二个char的低2位，20是第3个char的第5位，所以对应的结果就是3（8和9在同一char中）,16。

然后再来看我们最开始的问题。
用位图的话，就要开空间，40亿个数，以上面的逻辑，就会开2³² / 2³ + 1个char，也就是2²⁹ + 1
个char。

那么我们该怎么给N赋值呢？
两种方式，一种直接给-1，-1补码为全1，转成size_t就变成了2³² - 1个数。2³⁰是10多亿，乘以4就是40多亿，所以这样就是40多亿个数。还有一种是0xffffffff，也是全1。

然后我这里没有40多亿个数，就不演示怎么搞了，但我可以开一下任务管理器看看程序运行起来占了多少内存：

就是512MB。

bitset还有其他接口，但这上面的几个最重要，其他的就不模拟实现了。

几道关于位图的题目

再来几个问题：

1. 给定100亿个整数，设计算法找到只出现一次的整数？
2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？
3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整
   数

我们挨个来说。

给定100亿个整数，设计算法找到只出现一次的整数？

这里就要用位图了。但是和上面有点不一样，看题，100亿个整数，整数是有范围的：42亿多个数，题目中给100亿个数，那么就一定会有重复的数，所以说题中让我们找只出现一次的数。

我们把bitset改进一下，用两个bit位表示一个数就行了，00表示某个数没有出现，01表示某个数出现了一次，10表示某个数出现了两次以及两次以上。11就不用了。

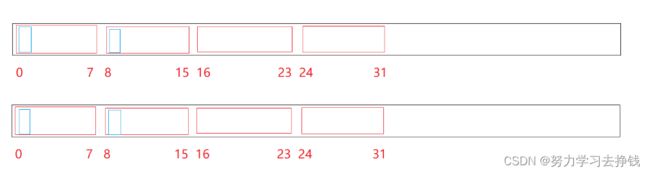
但是用一个位图的话算起来稍微麻烦一点，我们可以用两个位图，一个表示某一个数的xx两位中的高位，一个用来表示xx两位中的低位：

如图中蓝色框位置，上面表示低位，下面表示高位（或者反过来）。

那么我们来模拟实现一下：

print_once_num就是打印一下出现一次的数。

再来看下一题：

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

还是位图，用两个个512MB的位图将两个文件中给的数统计一下，然后让后让两个位图对应位置相与，得到的结果就是交集。

位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整
数

这就是第一个问题的变种，用两个位表示一个数，00、01、10都有效11就表示超过两次的。不细说了。

我们再来看看STL库中的位图：

好多接口，但set、reset、test最有用。

位图优点就是非常快，而且节省空间。但是只能映射整数，这一点比较局限。

下面来说说布隆过滤器。

布隆过滤器

概念

将哈希与位图结合，即布隆过滤器。

位图可以用来查找整数在不在。
布隆过滤器还能用来查找字符串在不在。

前一篇博客中，模拟实现哈希里面就用到了字符串哈希算法，里面有BHDK方法来让字符串转换成一个下标位置。这里布隆过滤器就是用一下字符串哈希算法，然后将对应的数字转换成下标位置，对应到数组中即可。

来个例子：假如现在要记录一下几个公司的名称，比如百度、字节、 美团等等。

现在再登记一个B站，登记前要判断一下之前是否登记过了，假如B站和美团计算出来的位置重复了，那么就会导致误判：

这就是布隆过滤器的一个缺点，如果原字符串没登记，但是判断出在了就会导致误判，判断出不在才是准确的。

那这样就太坑了，怎样改改不让重复呢？

完全不重复是不太可能的，但是我们可以降低重复率。
可以采用多个字符串哈希函数，从而让每个字符串映射出多个不同的位置。比如说每个字符串映射三个位置：

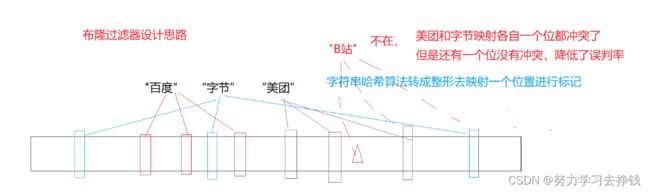
这样就能降低误判率，让每个值多映射几个位，理论而言，一个值映射的位越多，误判的概率越低，但也不能映射太多，映射位越多，空间消耗越多。

实例

在来两个例子吧。

失信名单

假如说你接到了一个电话，而且是诈骗电话，怎样在你还未接到电话的时候就显示出其是一个诈骗电话？

一般来说，这些失信名单/诈骗分子电话信息都是存储在数据库中的，而数据库一般都是在本地磁盘上或远端的，如果直接去数据库中找，效率太低了，我们可以提前搞一个布隆过滤器。

如果布隆过滤器中显示当前号码为诈骗电话，再到数据库中确认就行。如果显示不是，那就一定不是。

这样做就能大大提升查找效率。

注册名称

我们进一个网站注册账号，注册账号时需要让我们输入昵称，怎样快速判断当前昵称是否重复了/违规了呢？

还是布隆过滤器，但是这里可以不用判断那么仔细。

如果你当前输入的昵称过滤后显示重复了，那么就直接提示你名称重复/违规了，需要重新输入，不需要再仔细比对了，因为换个昵称还是没那么费事的。如果没有提示重复/违规，那就定了。

这样也能提高查找效率，同时也允许误判。

STL库中并未提供布隆过滤器。

但是我们还是要模拟实现一下的。

布隆过滤器模拟实现

上面也说了，同一个字符串要经过不同的哈希函数映射出不同的下标位置的，那么就需要搞多个哈希函数了，我这里就直接用上一篇文章中的了：

这里用三个哈希函数：

struct HashBKDR
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t val = 0;
		for (auto ch : key)
		{
			val *= 131;
			val += ch;
		}

		return val;
	}
};

struct HashAP
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t hash = 0;
		for (size_t i = 0; i < key.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ key[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ key[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};

struct HashDJB
{
	// BKDR
	size_t operator()(const string& key)
	{
		size_t hash = 5381;
		for (auto ch : key)
		{
			hash += (hash << 5) + ch;
		}

		return hash;
	}
};

然后我们还需要确定布隆过滤器要开多大的空间。因为随着插入元素的增多，空间开小了就会导致误判率提高，空间开大了就会导致浪费。

这里有一篇文章，内部就讲了关于哈希函数个数、插入元素个数以及布隆过滤器大小之间的关系，感兴趣的同学看看：详解布隆过滤器的原理，使用场景和注意事项。

我这里就直接截取其中的内容来用了：

我也在上面图中标记了，如果我们想要用3个哈希函数，那么布隆过滤器的长度就得是n的4.2倍，我就不按照4.2倍来了，直接给5倍。

框架：

注意上面得用const static才能在类内这样写，不然会报错的。因为浮点数、类对象以及字符串是不允许作为非类型模板参数的，只能是整形，而且传参时必须传常量。非类型的模板参数必须在编译期就能确认结果。

然后和位图一样，先搞set接口。

就把映射出的各个位置置为1就行了，但是要注意字符串哈希最后得到的数字可能会很大而导致超过了布隆过滤器的长度，所以要用除留余数法来使得得到的数在正确范围内。

然后就是test：

注意只有false返回的才是绝对正确的，当返回true的时候，不一定正确，可能会误判。

下面就用如下代码测试一下：

BloomFilter<10> bf;
string arr1[] = { "苹果", "西瓜", "阿里", "美团", "苹果", "字节", "西瓜", "苹果", "香蕉", "苹果", "腾讯" };

for (auto& str : arr1)
{
	bf.Set(str);
}

for (auto& str : arr1)
{
	cout << bf.Test(str) << ' ';
}
cout << endl << endl;

string arr2[] = { "苹果111", "西瓜", "阿里2222", "美团", "苹果dadcaddxadx", "字节", "西瓜sSSSX", "苹果 ", "香蕉", "苹果$", "腾讯" };

for (auto& str : arr2)
{
	cout << str << ":" << bf.Test(str) << endl;
}

结果如下：

上方并没有出现误判的情况。

误判率测试

再来写一个测试误判率的程序：

void TestBloomFilter2()
{
	srand(time(0));
	const size_t N = 1000000;
	BloomFilter<N> bf;

	std::vector<std::string> v1;
	std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";

	for (size_t i = 0; i < N; ++i)
	{
		v1.push_back(url + std::to_string(1234 + i));
	}

	for (auto& str : v1)
	{
		bf.Set(str);
	}

	// 相似
	std::vector<std::string> v2;
	for (size_t i = 0; i < N; ++i)
	{
		std::string url = "http://www.cnblogs.com/-clq/archive/2021/05/31/2528153.html";
		url += std::to_string(1234 + i);
		v2.push_back(url);
	}

	size_t n2 = 0;
	for (auto& str : v2)
	{
		if (bf.Test(str))
		{
			++n2;
		}
	}
	cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;

	std::vector<std::string> v3;
	for (size_t i = 0; i < N; ++i)
	{
		string url = "zhihu.com";
		url += std::to_string(rand() + i);
		v3.push_back(url);
	}

	size_t n3 = 0;
	for (auto& str : v3)
	{
		if (bf.Test(str))
		{
			++n3;
		}
	}
	cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}

在布隆过滤器大小是插入数据的五倍的时候：

10万个数：

100万个数：

在布隆过滤器大小是插入数据的十倍的时候：

10万个数：

100万个数：

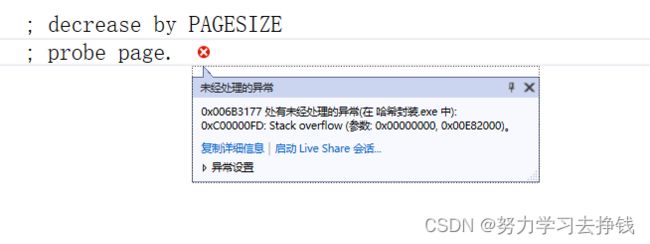
程序挂掉了。。
调试起来发现栈溢出了：

原因是STL库中实现的bitset是用静态数组实现的，所以刚执行程序光是数组就会在栈中开非常大的空间，所以就会导致栈溢出。

想要解决的话，就得在堆中开空间。两种方法。
一种是用我们自己实现的bitset：

另一种是还用库中的bitset，但是要改成指针，同时把类中用.调用的函数改为用->调用。

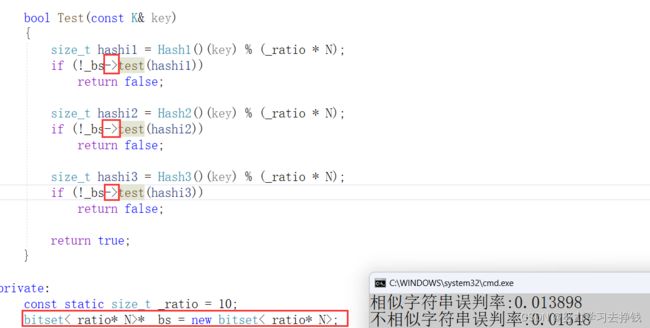
可以看到，布隆过滤器越长，误判率就越低，但是效率会变慢。

再来说一下布隆过滤器的reset。
直接说了，其实布隆过滤器不支持reset，因为一个字符串reset了可能会影响到其他字符串，想要解决这个问题的话，给每一个位置多给几个位，用来做引用计数，但是这样就会导致更多的空间消耗，从而就使得布隆过滤器的优势削弱了。所以说布隆过滤器一般是不支持删除的。这里也就不讲了。

几道题

1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出
   精确算法和近似算法
2. 如何扩展BloomFilter使得它支持删除元素的操作
3. 给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？
4. 与上题条件相同，如何找到top K的IP？

还是挨个来说：

1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出
   精确算法和近似算法

这道题先说近似算法，就是布隆过滤器。query就是网络请求、sql语句什么的，本质上都是字符串。那么我们就可以先让一个文件中的query先翻到一个布隆过滤器中，然后让另一个文件中的query在布隆过滤器中查找。

再说精确算法。要用到哈希切分（先不说是什么意思）。
我们来假设两个条件。

1. 假设每个query为30Byte，100亿个query就是3000亿个Byte，那么大概就是300个G。
2. 假设两个文件名为A和B。

如果将两个文件均分为300个小文件的话，先将A中的一个小文件加载到布隆过滤器中，再从B中的每个小文件进行查找，由此可见，效率非常低下。

但是如果我们将每个字符串哈希后，再经过除留余数法（假如说%的是1000）后结果相同的字符串放到一个小文件中呢？
.
比如说A中的一大堆字符串经过哈希算法之后得到的结果是394，那么就将这些字符串全部放到A的第394号文件中。B中同理。把每一个小文件都表上各自的序号，Ai和Bi（i为从0到999的整数）。
.
经过哈希算法之后，A和B两个大文件就各自分出了1000个小文件，并且每个标号相同的AB小文件中字符串哈希后的结果都相同。
.
那么我们就能让标号相同的文件中的字符串进行对比，比如说A0和B0，两文件中字符串哈希后的结果都相同，那么相同的字符串就一定在标号相同的文件中。让对应标号的AB文件进行对比，这样查找效率一下子就上来了。

上面将对应哈希后的结果放到同一文件中，这就是哈希切分。

2. 如何扩展BloomFilter使得它支持删除元素的操作

上面将布隆过滤器的最后已经说过了，这里就不多提了。

3. 给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

这里也是要用到哈希切分。IP地址也是可以用哈希算法来得到对应位置的。

只要把IP哈希后结果相同的放到同一个小文件中就行，这样就一定能让相同的IP地址存到一个小文件中，然后再在每个小文件中统计一下出现的次数最多的就行，将挨个文件中最多的进行对比，直到找到最后一个小文件为止。

4. 与上题条件相同，如何找到top K的IP？

还是上面的方法，不过是要用一下小堆（至于为啥是小堆就不讲了，TOPK问题，这在我前面数据结构的博客中有）。

该讲的都讲了。

到此结束。。。