因果推断dowhy之-医学案例中的反事实分析

0x01. 背景

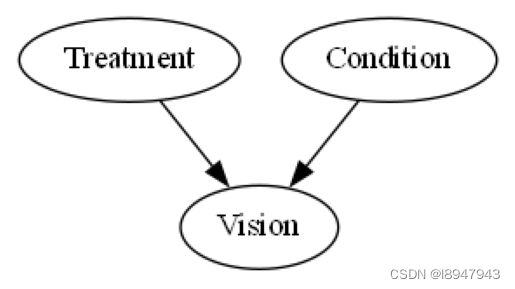
在这个例子中，我们知道三个观察变量的因果结构，我们想得到一些反事实的问题，例如“如果我采用了医生的不同建议，会发生什么?”

更具体地说，患有严重眼干症的爱丽丝决定使用远程在线医疗平台，因为她无法在自己居住的地方看眼科医生。她通过报告自己的病史来判断爱丽丝是否患有罕见的过敏症，平台最后为她推荐了两种可能的眼药水，成分略有不同(“选项1”和“选项2”)。

爱丽丝在网上快速搜索了一下，她发现选项1有很多积极的评价。尽管如此，她还是决定使用第二种方法，因为她的母亲过去也使用过这种方法，而且效果很好。几天后，爱丽丝的视力好多了，症状也开始消失。然而，她很好奇，如果她使用了非常流行的选项1，甚至什么都不做，会发生什么。

该平台为用户提供了反事实问题的可能性，只要他们报告他们所遵循的选项的结果。

0x02. 模拟数据

我们描述SCM框架如下，$f_{p1,p2}$是对模型增加的噪声，表示为：$Vision=V_n+f_{p1,p2}(Treatment,Condition)$。我们对三个观测变量的原始特征$N_T,N_C,N_V$加噪声进行采样，目标变量的Vision则是$N_V$加上其输入节点的噪声。

$Treatment=N_T$~0,1或2的概率分别为33%：33%的用户什么都不做，33%的用户选择选项1,33%的用户选择选项2。这与患者是否患有罕见疾病无关。

$Condition=N_C$~伯努利(0.01)：患者是否有罕见病。

$Vision=N_V+f_{p1,p2}(Treatment,Condition)=N_V-P_1(1-Condition)(1-Treatment)(2-Treatment)+2P_2(1-Conditon)Treatment(2-Treatment)+P_2(1-Condition)(3-Treatment)(1-Treatment)Treatment-2P_{2}ConditonTreatment(2-Treatment)-P_{2}Conditon(3-Treatment)(1-Treatment)Treatment$

$P_1$是一个常数，在患者没有罕见的情况下，原始视力会下降，他没有服用任何药物。

$P_2$是一个常数，根据患者是否患有这种疾病以及他们将使用的滴剂类型，原始视力将相应地增加或减少。更具体地说:

If Condition = 0 and Treatment = 1 then Vision = N_V + P_2

elIf Condition = 0 and Treatment = 2 then Vision = N_V - P_2

elIf Condition = 1 and Treatment = 1 then Vision = N_V - P_2

elIf Condition = 1 and Treatment = 2 then Vision = N_V + P_2

elIf Condition = 0 and Treatment = 0 then Vision = N_V - P_1

elif Condition = 1 and Treatment = 0 then Vision = N_V - P3

对于这样的罕见事件，比如有条件(condition =1，有1%的低概率)，需要有大量的样本来训练模型，以便准确地反映这些罕见事件。这就是为什么我们在这里使用10000个样本来生成患者数据库。

生成正常数据：

from scipy.stats import bernoulli, norm, uniform
import numpy as np
from random import randint
import pandas as pd

n_unobserved = 10000
unobserved_data = {
   'N_T': np.array([randint(0, 2) for p in range(n_unobserved)]),
   'N_vision': np.random.uniform(0.4, 0.6, size=(n_unobserved,)),
   'N_C': bernoulli.rvs(0.01, size=n_unobserved)
}
P_1 = 0.2
P_2 = 0.15

def create_observed_medical_data(unobserved_data, name):
    observed_medical_data = {}
    observed_medical_data['Condition'] = unobserved_data['N_C']
    observed_medical_data['Treatment'] = unobserved_data['N_T']
    observed_medical_data['Vision'] = unobserved_data['N_vision'] + (-P_1)*(1 - observed_medical_data['Condition'])*(1 - observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (2*P_2)*(1 - observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (P_2)*(1 - observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(1 - observed_medical_data['Treatment'])*(3 - observed_medical_data['Treatment']) + 0*(observed_medical_data['Condition'])*(1 - observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (-2*P_2)*(unobserved_data['N_C'])*(observed_medical_data['Treatment'])*(2 - observed_medical_data['Treatment']) + (-P_2)*(observed_medical_data['Condition'])*(observed_medical_data['Treatment'])*(1 - observed_medical_data['Treatment'])*(3 - observed_medical_data['Treatment'])
    dfs = pd.DataFrame(observed_medical_data)
    dfs.to_csv(name, index=False)
    return pd.DataFrame(observed_medical_data)

medical_data = create_observed_medical_data(unobserved_data, 'patients_database.csv')

生成异常数据：

num_samples = 1
original_vision = np.random.uniform(0.4, 0.6, size=num_samples)
def generate_specific_patient_data(num_samples):
    return create_observed_medical_data({
    'N_T': np.full((num_samples,), 2),
    'N_C': bernoulli.rvs(1, size=num_samples),
    'N_vision': original_vision,
})

specific_patient_data = generate_specific_patient_data(num_samples, "newly_come_patients")

0x03. 读取正常数据

我们有一个由三个观察变量组成的数据库:一个从0到1的连续变量，表示视力质量(“Vision”)，一个二元变量，表示患者是否患有罕见疾病(即过敏)(“condition”)，以及一个类别变量(“Treatment”)，可以取三个值(0:“什么都不做”，1:“选项1”或2:“选项2”)。数据如下:

import pandas as pd

medical_data = pd.read_csv('patients_database.csv')
medical_data.head()

数据如下：

	Condition	Treatment	Vision
0	0	2	0.223475
1	0	2	0.197306
2	0	0	0.101252
3	0	1	0.703056
4	0	0	0.020249

medical_data.iloc[0:100].plot(figsize=(15, 10))

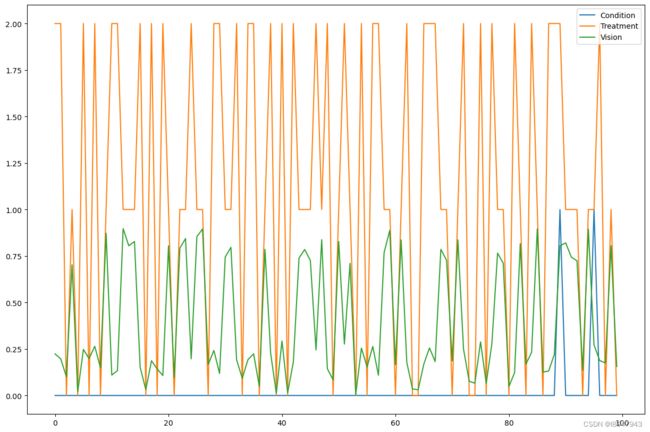
数据集反映了患者在采取三种治疗方案之一后的视力，这是基于他们是否患有罕见疾病。请注意，数据集没有关于治疗前患者原始视力的信息(即vision变量的噪声)。正如我们将在下面看到的，只要我们有后非线性模型(例如ANM)，视觉的噪声部分就会被反事实算法恢复。

0x04. 建模

我们知道“治疗”节点和“条件”节点导致了视觉，但我们不知道结构上的因果模型。然而，我们可以从观测数据中了解到它。我们假设这个图表正确地代表了因果关系，并且我们假设没有隐藏的混杂因素(因果充足性)。根据给定的图表和数据，我们可以拟合因果模型，并开始回答反事实的问题。

import networkx as nx
import dowhy.gcm as gcm

causal_model = gcm.InvertibleStructuralCausalModel(nx.DiGraph([('Treatment', 'Vision'), ('Condition', 'Vision')]))
gcm.auto.assign_causal_mechanisms(causal_model, medical_data)

gcm.util.plot(causal_model.graph)

gcm.fit(causal_model, medical_data)

0x05. 读取异常数据

specific_patient_data = pd.read_csv('newly_come_patients.csv')
specific_patient_data.head()

输出如下：

	Condition	Treatment	Vision
0	1	2	0.857103

0x06. 回答爱丽丝的反事实问题

如果我们想要检查一个假设的结果，如果一个事件没有发生，或者发生的方式不同，我们会使用所谓的基于结构性因果模型的反事实逻辑。考虑到-我们知道爱丽丝的治疗方案是第二种。爱丽丝患有罕见的过敏(条件=1)。治疗方案2后，爱丽丝视力为0.78(视力=0.78)。-我们能够根据学习到的结构因果模型恢复噪声。

如果治疗节点不同，我们现在可以检查她的视觉的反事实结果。在下面，我们来看看如果爱丽丝没有接受任何治疗(治疗=0)，如果她服用了其他眼药水(治疗=1)，爱丽丝的视力的反事实值。

counterfactual_data1 = gcm.counterfactual_samples(causal_model,
                                                  {'Treatment': lambda x: 1},
                                                  observed_data = specific_patient_data)

counterfactual_data2 = gcm.counterfactual_samples(causal_model,
                                                  {'Treatment': lambda x: 0},
                                                  observed_data = specific_patient_data)


import matplotlib.pyplot as plt

df_plot2 = pd.DataFrame()
df_plot2['Vision after option 2'] = specific_patient_data['Vision']
df_plot2['Counterfactual vision (option 1)'] = counterfactual_data1['Vision']
df_plot2['Counterfactual vision (No treatment)'] = counterfactual_data2['Vision']

df_plot2.plot.bar(title="Counterfactual outputs")
plt.xlabel('Alice')
plt.ylabel('Eyesight quality')
plt.legend()

效果如下：

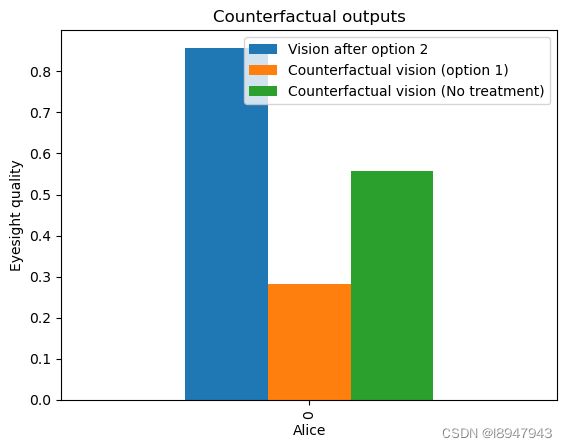
我们在这里看到的是，如果Alice选择了选项1，她的视力会比选项2更差。因此，她意识到她在病史中报告的罕见情况(条件=1)可能会导致对流行选项1的过敏反应。爱丽丝还可以看到，如果她没有选择任何推荐的选项，她的视力会比她选择的选项2更差(变量Vision导致的相对值更小)。