背包问题 - 动态规划
1. 背包问题总结
暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
背包问题是动态规划(Dynamic Planning) 里的非常重要的一部分,关于几种常见的背包,其关系如下:
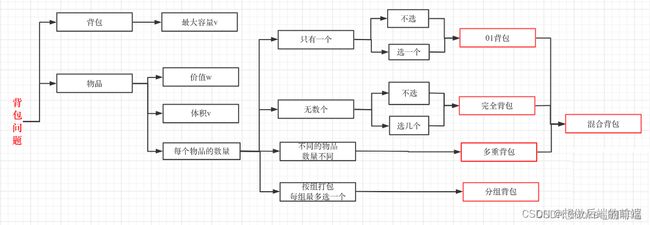
2. 01背包
01背包问题是最基础的背包问题类型,它的特点是每种物品都只有一个,可以选择装入背包或不装入背包。每个物品的体积是vi,价值是wi,背包的体积是V。现在要求在不超过背包体积的情况下,选取物品的价值最大。
为理解此问题的实质,下面我用一个实际例子来进行讲解。假设现在有以下3件物品,以及一个容量为4的背包,现在你想知道,你的背包所能装下的最大价值是多少
| 物品名称 | 体积 | 价值 |
|---|---|---|
| airpods | 1 | 1500 |
| iwatch | 2 | 2000 |
| iphone | 3 | 3000 |
最简单的办法,我们可以将这3件物品的所有组合枚举出来,然后求出每种组合的价值,最终输出最大值即可。高中时大家都学过集合,我们知道,对于某个具有n个元素的集合Φ,其子集个数为2n。也就是说对于有n件物品的集合,其可能的组合方案有2n个。比如对于上面这3件物品,其可能的组合就有23=8个,如下
| 组合方案 | 总容量 | 总价值 |
|---|---|---|
| {} | 0 | 0 |
| {airpods} | 1 | 1500 |
| {iwatch} | 2 | 2000 |
| {iphone} | 3 | 3000 |
| {airpods,iwatch} | 3 | 3500 |
| {airpods,iphone} | 4 | 4500 |
| {iwatch,iphone} | 5 | 5000 |
| {airpods,iwatch,iphone} | 6 | 6500 |
接下来我们将其中满足总容量不大于4的组合方案选出,并将其作为一种合法的选取,于是可以得到此类方案对应的总价值集合:{ 0,1500,2000,3000,4500 },最终取出其中的最大值4500即可(经验证,此为正确答案,即选择组合{ airpods,iphone})。
这样的算法很容易理解,但是弊端非常大:严重耗时。比如当待选物品有100件时,此时总的组合方案数将达到2100个,要枚举这所有的组合必然超时。而实际上,对于100件物品而言,这个数据范围却并不大,所以上面的枚举法是行不通的。
而动态规划算法的基本思想是将待求解问题分解成若干个子问题,然后再将这些子问题分阶段处理以避免重复计算来进行求解的。这里面最关键的一步,在于寻找问题的动态转移方程(即递推式)。接下来,我们依然通过填表来寻找这一规律,先将背包问题的网格绘出,如下:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | ||||
| iwatch | ||||
| iphone |
其中每列表示容量不同的背包,每行表示当前可以选择的物品。
其中每个格子的含义为(假设当前为第i行、第j列):在当前背包容量为j、可选第i行及其之前的所有物品(按序排列)的前提下,能够选到的最大价值。
接下来我们需要填充其中的每个单元格,当网格填到最后一行最后一列时,即求到了在容量为V、可选所有商品的条件下背包所能容纳的最大价值。
首先是第一行(可选airpods),我们需要尝试把airpods装入背包以使背包的价值最大。在每个单元格,都需要做一个简单的决定:要不要airpods?别忘了,你要找出一个价值最高的商品集合。第一个单元格表示背包的容量为1,耳机的体积也是1,这意味着它能装入背包!因此,这个单元格包含耳机,价值为1500。于是可以填充网格,如下图所示:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | |||
| iwatch | ||||
| iphone |
与第一个单元格相同,每个单元格都将包含当前可装入背包的所有商品。来看下一个单元格,这个单元格表示背包的容量为2,完全能够装下airpods!并以此类推第一行的所有单元格均可装下airpods
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | ||||
| iphone |
现在你很可能心存疑惑:原来的问题说的是容量为4的背包,我们为何要考虑容量为1、2、3的背包呢?前面说过,动态规划是从小问题着手,逐步解决大问题。这里解决的子问题将帮助后面我们解决大问题。其实这正是体现动态转移的一个方面。
接下来填充第二行(可选airpods、iwatch)。我们先看第一个单元格,它表示容量为1的背包。在此之前,可装入容量为1的背包的商品最大价值为1500。现在面临一个新问题:该不该拿iwatch呢?当前背包的容量为1,能装下iwatch吗?太大了,装不下!由于容量1的背包装不下iwatch,因此最大价值依然是1500,如下:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | |||
| iphone |
接下来第二个单元格的容量为2可以装下iwatch,并且iwatch的价值比airpods大,所以我们装iwatch:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | 2000 | ||
| iphone |
接下来第三四个单元格的容量为3和4可以同时装下airpods和iwatch了,并且价值肯定是最大的, 所以我们装都装下:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | 2000 | 3500 | 3500 |
| iphone |
然后就是第三行了,前两个单元格,我们之前都知道按照之前的计算就能得出:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | 2000 | 3500 | 3500 |
| iphone | 1500 | 2000 |
当到了第三个单元格,我们就能装下iphone了。但是iphone的价值是3000,而如果放airpods和iwatch价值是3500。当然这里不用再次计算airpods和iwatch的价值了,因为通过第二行的第三个单元格,我们就可以知道,所以我们此时不放iphone,最大价值仍然是3500:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | 2000 | 3500 | 3500 |
| iphone | 1500 | 2000 | 3500 |
到了第四个单元格了,我们可以选择iphone,并且选完后仍然有一个容量可以放airpods他们的价值是4500:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 1500 | 1500 | 1500 |
| iwatch | 1500 | 2000 | 3500 | 3500 |
| iphone | 1500 | 2000 | 3500 | 4500 |
注:在计算最后一个单元格的最大价值时,我们选择拿iphone,此时还剩下1的容量,于是我们直接加上该行单元格中的第一个单元格内容(即3000+1500)便得到了这种方案下的总价值,最后再与之前的总价值(即3500)比较大小,并将较大者写入其中。这一操作,实际上就体现了动态转移的思想(以递推的方式取代递归求解)。
dp[i][j] = max( 上方单元格的价值,剩余空间的价值 + 当前商品的价值 )
= max( dp[i-1][j],dp[i-1][j-当前商品的体积] + 当前商品的价值 )
= max( dp[i-1][j],dp[i-1][j-w[i]] + v[i] )
看算法:
function maxBagProfit(){
const weights = [1,2,3]
const values = [15,20,30]
const bagWeight = 4
let dp = new Array(weights.length).fill(0).map(x=> new Array(bagWeight+1).fill(0));
console.log("创建数组",dp)
for (let i = bagWeight; i >= weights[0]; i--) {
dp[0][i] = dp[0][i-weights[0]] + values[0];
}
console.log("初始化数组",dp)
for (var i = 1; i < weights.length; i++) {
for (var j = 0; j <= bagWeight; j++) {
if (j < weights[i]) {
dp[i][j] = dp[i - 1][j];
}
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);
}
}
}
console.log("背包数组",dp)
return dp[weights.length - 1][bagWeight]
}
2. 完全背包
完全背包问题是背包问题的一个变种,其特点在于每种物品有无限个。
和01背包问题不同,01背包每种物品只能选择一次,而完全背包每种物品可以选择多次,甚至可以不选择。每个物品有体积vi和价值wi,背包的容量为V,目标是在不超过背包容量的前提下,选取物品的总价值最高。
我们还是用上面的例子来解释,因为我真的有airpods,iwatch,iphone,除此之外还有ipad和MacBook Pro当然ipencil也有了纯粹题外话过渡下。但是这里我要调整下iwatch和iphone的价格不然全选aipods就是最优解,再进行下面的推演就没有意义了。
| 物品名称 | 体积· | 价值 |
|---|---|---|
| airpods | 1 | 1500 |
| iwatch | 2 | 3200 |
| iphone | 3 | 5000 |
首先是第一行只能选airpods,所以根据数量无脑填充,如下图所示:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | ||||
| iphone |
接着是第二行,我们可选的多了iwatch,对于第一个单元格只能选airpod,而而第二个就可以选iwatch了并且iwath的价值是大于两个aipods:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | ||
| iphone |
到了第三个单元格时这时就是组合价值最高了
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | 4700 | |
| iphone |
而第四个单元格就变复杂了,我们有两种选择方案,并且他们的价值都比上一行单元格的价值大,第一种是选一个iwatch和两个airpods他们的价值和是6200,而选两个iwatch是6400,所以就是两个iwatch(但是这里的算法显然就和之前的不一样了呀,应该怎么解决呢?)
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | 4700 | 6400 |
| iphone |
到了第三行,前两个单元格放不下iphone,所以我们还是用上一行的替代:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | 4700 | 6400 |
| iphone | 1500 | 3200 |
到了第三个单元格可以放下iphone并且价值最高:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | 4700 | 6400 |
| iphone | 1500 | 3200 | 5000 |
到了最一个单元格,这里的可选方案就有选择iphone和一个airpods价值最大(到这里我已经想明白了上面疑问,其实不是有两种方案,而是始终只有一种方案就是选择两个iwatch,因为如果这个方案的价值小于四个airpod的话,那就说明就算选一个iwatch和两个airpods的价值也是小于四个aippods的价值)所以结果就是
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 6000 |
| iwatch | 1500 | 3200 | 4700 | 6400 |
| iphone | 1500 | 3200 | 5000 | 6500 |
dp[i][j] = max( 上方单元格的价值,剩余空间的价值 + 当前商品的价值*当前商品的数量 )
dp[i][j] = max( dp[i-1][j] , dp[i-1][ j - kw[i] ] + kv[i] )
看算法:
function maxBagProfit(){
const weights = [1,2,3]
const values = [15,32,50]
const bagWeight = 4
let dp = new Array(weights.length).fill(0).map(x=> new Array(bagWeight+1).fill(0));
console.log("创建数组",dp)
for (let i = bagWeight; i >= weights[0]; i--) {
dp[0][i] = dp[0][i-weights[0]] + values[0]*Math.floor(i/weights[0]);
}
console.log("初始化数组",dp)
for (var i = 1; i < weights.length; i++) {
for (var j = 0; j <= bagWeight; j++) {
if (j < weights[i]) {
dp[i][j] = dp[i - 1][j];
}
else {
let num = Math.floor(j/weights[i]);
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i]*num] + values[i]*num);
}
}
}
console.log("背包数组",dp)
return dp[weights.length - 1][bagWeight]
}
3. 多重背包
多重背包问题是背包问题中更一般化的问题。在多重背包问题中,每种物品不再是只有一个或者无限个,而是有限个,数量为mi。
每个物品有体积vi和价值wi,背包的容量为V。现在要求背包装下的物品价值最大。更具体地,我们要确定每种物品应该选取多少个,才能使得选取的物品的体积不超过背包容量,同时使得价值最大。
不嫌麻烦的话可以继续看下面的推演,或者直接看结论。
这里的推演我们还是用01背包的数据,但是要加上数量限制:
| 物品名称 | 体积 | 价值 | 数量 |
|---|---|---|---|
| airpods | 1 | 1500 | 3 |
| iwatch | 2 | 2000 | 2 |
| iphone | 3 | 3000 | 1 |
这时候由于数量限制第一行的初始数据就变成了:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 4500 |
| iwatch | ||||
| iphone |
接着是第二行由于容量限制第一个单元格和上一个一样,第二个单元格选iwatch的话没有两个airpods的价值高,第三个单元格,选一个iwatch和一个airpods的价值低于三个airpods,所以还是不变:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 4500 |
| iwatch | 1500 | 3000 | 4500 | |
| iphone |
到了第四个单元格,两个iwatch是4000,低于三个aipods,但是一个iwatch和两个airpods就超过了,(这里就要开始矛盾了,因为正常来说按照上面的算法我是不会算到一个iwatch和两个airpods,那就在下个括号中看看我能不能反应过来吧)
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 4500 |
| iwatch | 1500 | 3000 | 4500 | 5000 |
| iphone |
到了第三行,前三个单元格直接可以比较得出和上一行的数据一样
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 4500 |
| iwatch | 1500 | 3000 | 4500 | 5000 |
| iphone | 1500 | 3000 | 4500 |
到了第四个单元格一个iphone和一个airpods的价值是4500小于5000,所以选5000
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| airpods | 1500 | 3000 | 4500 | 4500 |
| iwatch | 1500 | 3000 | 4500 | 5000 |
| iphone | 1500 | 3000 | 4500 | 5000 |
(针对上面提出的问题,我这里想出的方案就是再加上一层循环考虑所有的情况了)
dp[i][j] = max( 上方单元格的价值,剩余空间的价值 + 当前商品的价值*(1-当前商品的数量) )
dp[i][j] = max{dp[i-1][j], dp[i-1][j-vi]+wi, dp[i-1][j-2vi]+2wi, … , dp[i-1][j-ki*vi]+ki*wi},其中ki为 min{j/vi, mi}。
看算法:
function maxBagProfit(){
const weights = [1,2,3]
const values = [15,20,30]
const nums = [3,2,1]
const bagWeight = 4
let dp = new Array(weights.length).fill(0).map(x=> new Array(bagWeight+1).fill(0));
console.log("创建数组",dp)
for (let i = bagWeight; i >= weights[0]; i--) {
dp[0][i] = dp[0][i-weights[0]] + values[0]* Math.min(nums[0],Math.floor(i/weights[0]));
}
console.log("初始化数组",dp)
for (var i = 1; i < weights.length; i++) {
for (var j = 0; j <= bagWeight; j++) {
if (j < weights[i]) {
dp[i][j] = dp[i - 1][j];
}
else {
let maxValue = dp[i - 1][j];
let num = Math.min(nums[i],Math.floor(j/weights[i]));
for (let k = 1; k <= num; k++) {
maxValue = Math.max(maxValue, (dp[i - 1][j - weights[i]*k] + values[i]*k));
}
dp[i][j] = maxValue;
}
}
}
console.log("背包数组",dp)
return dp[weights.length - 1][bagWeight]
}
4.总结
01背包问题与完全背包问题实际上是两种极端,而多重背包问题则正是介于这两者之间的一种情况。基于此,我们可以将多重背包问题转化为01背包或完全背包问题来进行求解。
- 可以把某种物品中的k个视为k种不同物品,此时再对所有物品按照01背包问题来进行处理。这样的转化当然是成立的,但是仅在数据范围较小时才适用,一旦每种物品的数量稍大一点,在时间上必然有超时的风险。此时,对于某种物品(假设有k个),若我们采用一种更精炼的划分方案,就会使得该物品分类下来的组数大大减少。比如可以采用二进制的拆分将原来的k个物品分为:{
1、2、4、……、k - 2i + 1 } 这些组,以替代最初的分类:{ 1、1、1、……、1 }
这些组,这是一个log2(n)级别的数量优化。 - 若存在某个物品,其数量k乘以其单位体积大于背包总容量(即k*w[i] > V),那么此时对于该物品而言,它与背包之间是完全背包问题。
上述两点分别从01背包和完全背包的角度对多重背包问题进行了转化,而多重背包正好也是介于01背包和完全背包之间的问题。正是这两点,使得我们能设计出一个可以与“单调队列优化”分庭抗衡的算法。下面还是用一个实际例题来练手,以巩固理解。最后对于分组背包知道就好。