因果推断（三）双重差分法（DID）

因果推断（三）双重差分法（DID）

双重差分法是很简单的群体效应估计方法，只需要将样本数据随机分成两组，对其中一组进行干预。在一定程度上减轻了选择偏差带来的影响。

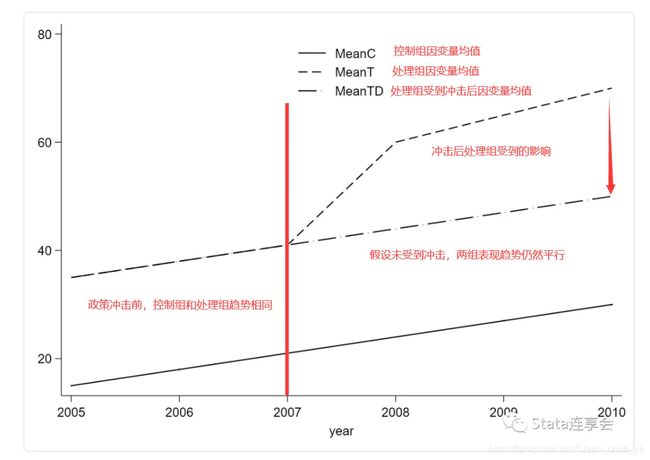
因果效应计算：对照组y在干预前后的均值差（${\bar{A}}_2-{\bar{A}}_1$），实验组y在干预前后的均值差（${\bar{B}}_2-{\bar{B}}_1$），则因果效应：$({\bar{B}}_2-{\bar{B}}_1)-({\bar{A}}_2-{\bar{A}}_1)$

假设前提：DID有一个很重要且很严格的平行趋势假设，即实验组和对照组在没有干预的情况下，结果的趋势是一样的。

准备数据

from faker import Faker
from faker.providers import BaseProvider, internet 
from random import randint
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import statsmodels.formula.api as smf
import warnings

warnings.filterwarnings('ignore')

# 绘图初始化
%matplotlib inline
sns.set(style="ticks")

# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
    def myCityLevel(self):
        cl = ["一线", "二线", "三线", "四线+"]
        return cl[randint(0, len(cl) - 1)]
    def myGender(self):
        g = ['F', 'M']
        return g[randint(0, len(g) - 1)]
fake.add_provider(MyProvider)

# 构造假数据，模拟用户特征
uid=[]
cityLevel=[]
gender=[]
for i in range(10000):
    uid.append(i+1)
    cityLevel.append(fake.myCityLevel())
    gender.append(fake.myGender())
    
raw_data= pd.DataFrame({'uid':uid,
                        'cityLevel':cityLevel,
                        'gender':gender,
                       })

raw_data['class'] = raw_data['uid'].map(lambda x: 'A' if x % 2 == 1 else 'B') # 按奇偶随机分组

# 构造did数据
df = pd.DataFrame(columns=['uid','cityLevel','gender', 'class', 'sales', 'dt'])
for i,j in enumerate(range(2005,2011)):
    lift = 1+i*0.05
    df_temp = raw_data.copy()
    df_temp['sales'] = [int(x) for x in np.random.normal(300*lift, 60*lift, df_temp.shape[0])]
    df_temp['sales'] = df_temp.apply(lambda x: x.sales*0.88 if x['class']=='A' else x.sales, axis=1)
    if j>2007:
        df_temp['sales'] = df_temp.apply(lambda x: x.sales*(1+i*0.02) if x['class']=='B' else x.sales, axis=1)
    df_temp['dt'] = j
    df=pd.concat([df,df_temp])
    
df_did = df.groupby(['class', 'dt'])['sales'].sum().reset_index()

验证平行趋势假设

# 计算文字的y坐标
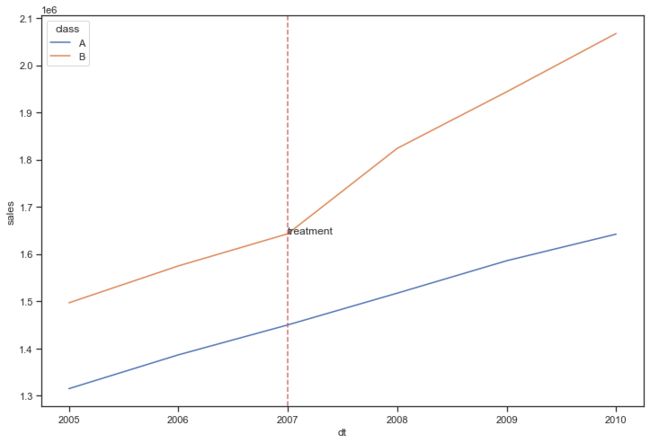
y_text = df_did.query('dt == 2007 and `class`=="B"')['sales'].values[0]
# 绘图查看干预前趋势
fig, ax = plt.subplots(figsize=(12,8))
sns.lineplot(x="dt", y="sales", hue="class", data=df_did)
ax.axvline(2007, color='r', linestyle="--", alpha=0.8)
plt.text(2007, y_text, 'treatment')
plt.show()

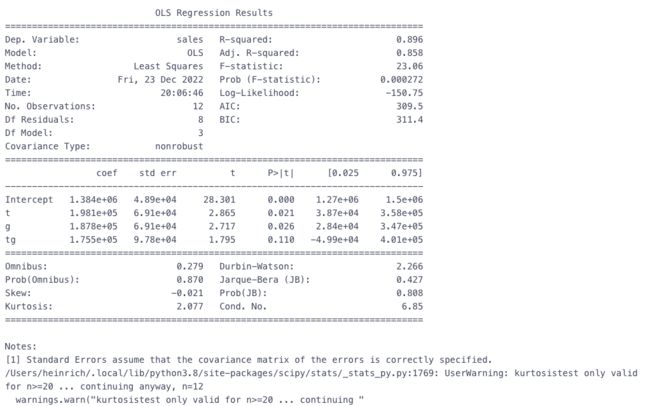
除了画图观察平行趋势，也可以通过回归拟合，参考自如何使用Python计算双重差分模型

# 方法2 回归计算
df_did['t'] = df_did['treatment'].map(lambda x: 1 if x=='干预后' else 0) # 是否干预后
df_did['g'] = df_did['class'].map(lambda x: 1 if x=='B' else 0) # 是否试验组
df_did['tg'] = df_did['t']*df_did['g'] # 交互项

# 回归
est = smf.ols(formula='sales ~ t + g + tg', data=df_did).fit() 
print(est.summary()) 

可以看到交互项tg并不显著，因此可以认为具备平行趋势

计算因果效应

# 计算因果效应
df_did['treatment'] = df_did['dt'].map(lambda x: '干预后' if x>2007 else '干预前')
df_did_cal = df_did.groupby(['class', 'treatment'])['sales'].mean()
did = (df_did_cal.loc['B', '干预后'] - df_did_cal.loc['B', '干预前']) - \
        (df_did_cal.loc['A', '干预后'] - df_did_cal.loc['A', '干预前'])
print(did)

175541.82000000007

总结

在实际业务中，平行趋势假设是很难满足的，因此常常会先进性PSM构造相似的样本，这样两组群体基本上就会符合平行趋势假设了，所以常见以PSM+DID进行因果推断，有兴趣的同学可以结合这两期的内容自行尝试。

共勉～