自回归模型的建模与参数估计-Python

AR§模型的参数估计

设{$X_t$}适合$X_t=a_1{X}_{t-1}+\cdots +a_p{X}_{t-p}+{ϵ}_t$,式中{${ϵ}_t$}为独立同分布白噪声序列；$E{ϵ}_t^2={\sigma }^2$，来自{$X_t$}的样本为$X_1，X_2，\cdots ，X_n$，要估计$a_1，a_2，\cdots ，a_p，{\sigma }^2$。

创建一个AR(2)过程

$$x_t=0.6x_{t-1}-0.75x_{t-2}+{ϵ}_t$$

import matplotlib.pyplot as plt
import numpy as np
from statsmodels.tsa.stattools import acf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

n = 5000
mean = 0
std = 1 
lag = 20

np.random.seed(0)
x_t = list(np.random.normal(mean, std, size=2))
epsilon_t = np.random.normal(mean, std, size=n) # 创建白噪声
for i in range(2, n+2):
    x_t.append(0.6 * x_t[i-1] - 0.75 * x_t[i-2] + epsilon_t[i-2])
# 绘制白噪声
plt.plot(x_t)
plt.title("AR2 process")
plt.show()

# 计算自相关函数(ACF)
plot_acf(x=x_t, lags=lag, title="ACF x_t")
plot_pacf(x=x_t, lags=lag, title="PACF x_t")
plt.show()

• 使用statsmodels模块估计参数和下文对比

# use statsmodel to fit this series
import statsmodels as sm
arma_mod20 = sm.tsa.arima.model.ARIMA(x_t, order=(2,0,0)).fit()
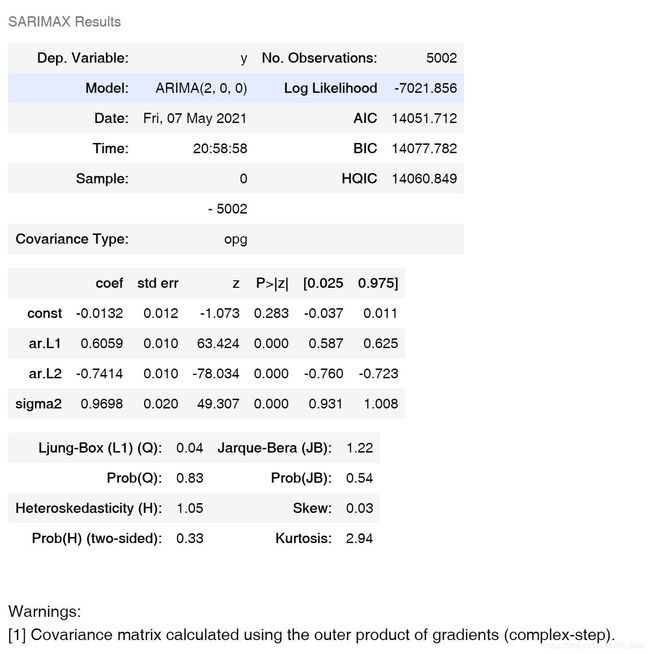
arma_mod20.summary()

输出：

其中const即是对时间序列样本均值进行估计

np.mean(x_t)

-0.01320250123146827

其他参数可以使用下面三种方法进行估计。

1. Yule-Walker 估计法
   由Yule-Walker方程：$b_p={\Gamma }_p\alpha$
   式中：
   $$b_p=\left[\begin{array}{c}{\gamma }_1\\ {\gamma }_2\\ ⋮\\ {\gamma }_p\end{array}\right],{\Gamma }_p=\left[\begin{array}{cccc}{\gamma }_0& {\gamma }_1& \cdots & {\gamma }_{p-1}\\ {\gamma }_1& {\gamma }_0& \cdots & {\gamma }_{p-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\gamma }_{p-1}& {\gamma }_{p-2}& ⋮& {\gamma }_0\end{array}\right],$$
   $$\alpha =\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_p\end{array}\right]$$
   ${\gamma }_k$为自协方差函数可以用样本的自协方差函数${\hat{\gamma }}_k$代替，然后可以计算参数$a_1，a_2，\cdots ，a_p$，${\sigma }^2$的Yule-Walker估计为
   $${\hat{\sigma }}^2={\hat{\gamma }}_0-{\hat{a}}_1{\hat{\gamma }}_1-\cdots -{\hat{a}}_p{\hat{\gamma }}_p$$ $$\left[\begin{array}{c}{\hat{a}}_1\\ {\hat{a}}_2\\ ⋮\\ {\hat{a}}_p\end{array}\right]={\left[\begin{array}{cccc}{\hat{\gamma }}_0& {\hat{\gamma }}_1& \cdots & {\hat{\gamma }}_{p-1}\\ {\hat{\gamma }}_1& {\hat{\gamma }}_0& \cdots & {\hat{\gamma }}_{p-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\hat{\gamma }}_{p-1}& {\hat{\gamma }}_{p-2}& ⋮& {\hat{\gamma }}_0\end{array}\right]}^{-1}\left[\begin{array}{c}{\hat{\gamma }}_1\\ {\hat{\gamma }}_2\\ ⋮\\ {\hat{\gamma }}_p\end{array}\right],$$
   自协方差函数
   $\gamma (h)=\text{cov}(X(t),X(t-h))=E[X(t)-{\mu }_t][X(t-h)-{\mu }_{t-h}]=E[X(t)X(t-h)]-{\mu }_t{\mu }_{t-h}$

def inverse_yule_walker_ar(x, p):
    """
    Implementation for a direct inverse solution on Yule-Walker equations
    @param x: the dataset, a numpy 1D array
    @param p: lags, p in AR(p)
    @return: a 1-D numpy array phi of shape p. phi[i] = parameter for x_{t-i} in a AR(p) model
    """
    # compute sample autovariance function
    x_bar = np.mean(x)
    covp = []
    for i in range(p+1):
        lenx = len(x)-i
        xt = x[i:]
        xtp = x[:lenx]
        covp.append(np.sum((xt-x_bar)*(xtp-x_bar))/len(x))
    # compute the p * p R_p matrix
    R_p = np.zeros([p,p])
    for j in range(p):
        for k in range(p):
            R_p[j,k] = covp[np.abs(j-k)]
    # compute phi = R_p^{-1} covp
    phi = np.linalg.inv(R_p).dot(np.array(covp[1:]))
    return phi

2. 最小二乘法
   $X_t=a_1{X}_{t-1}+\cdots +a_p{X}_{t-p}+{ϵ}_t$取$t=p+1,p+2,\cdots ,n$
   $$\left[\begin{array}{c}{X}_{p+1}\\ X_{p+2}\\ ⋮\\ X_n\end{array}\right]=\left[\begin{array}{cccc}{X}_p& X_{p-1}& \cdots & X_1\\ X_{p+1}& X_{p+2}& \cdots & X_2\\ ⋮& ⋮& \ddots & ⋮\\ X_{n-1}& X_{n-2}& ⋮& X_{n-p}\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_p\end{array}\right]+\left[\begin{array}{c}{ϵ}_{p+1}\\ {ϵ}_{p+2}\\ ⋮\\ {ϵ}_n\end{array}\right],$$
   用矩阵形式表示：$X=X\alpha +ϵ$
   应用回归分析中的最小二乘法：
   $\hat{\alpha }=(X^{T}X{)}^{-1}{X}^{T}Y$
   ${\hat{\sigma }}^2=\frac{1}{n-p}{Y}^T[I-X(X^{T}X{)}^{-1}{X}^T]Y$

def OLS_ar(x, p):
    """
    @param x: the dataset, a numpy 1D array
    @param p: lags, p in AR(p)
    @return: a 1-D numpy array phi of shape p. phi[i] = parameter for x_{t-i} in a AR(p) model
    """
    # construct Y
    lenx = len(x)-p
    Y = x[p:]
    X = np.zeros((lenx,p))
    for i in range(lenx):
        for j in range(p):
            X[i,j] = x[np.abs(p-j-1+i)]
    return np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)),X.T),Y)

3. 极大似然法
   设$\{{ϵ}_t\}$为正态白噪声序列，则$X^T=(X_1,X_2,\cdots ,X_n{)}^T\sim N_n(0,\mathbf{\Sigma })$,似然函数
   $$\begin{array}{rl}\text{ln}L(\mathbf{\alpha },{\sigma }^2)& =\text{ln}\frac{1}{(2\pi {)}^{n/2}|\mathbf{\Sigma }{|}^{1/2}}{\text{e}}^{-\frac{1}{2}{\mathbf{x}}^T{\mathbf{\Sigma }}^{-1}\mathbf{x}}\\ & =\text{ln}\frac{1}{(2\pi {)}^{n/2}}-\frac{1}{2}\text{ln}|\mathbf{\Sigma }|-\frac{1}{2}{\mathbf{x}}^T{\mathbf{\Sigma }}^{-1}\mathbf{x}\end{array}$$
   $\mathbf{\Sigma }$是$X^T$的协方差矩阵，是一个$n$阶正定实对称方阵，$|\mathbf{\Sigma }|$是$\mathbf{\Sigma }$的行列式
   证明详情不再赘述：https://blog.csdn.net/sunbobosun56801/article/details/99753664
   最后得到的结论即是极大似然估计和最小二乘估计和最小二乘估计结果是一致的。

参考文献

[1] 时间序列与多元统计分析(2016). 孙祝岭 编.
[2] https://github.com/charlieblue17/timeseries2018