RSA基本原理及常见攻击方法

1前言

密码学为数据的处理、存储和通信过程提供附加的安全级别。近年来，数学家和计算机科学家开发了一系列日益复杂的算法，这些算法被设计用于确保机密性、完整性、身份认证和不可否认性。在密码学家花费大量时间开发强加密算法的同时， 黑客们和政府同样投入了可观的资源来破解这些密码学算法。这产生了密码学领域的"军备竞赛"，并且导致如今使用的极其精密的算法的不断发展。

2现代密码学中的RSA

        “现代密码学”的主体可以分为“对称密码学”和“非对称密码学”。

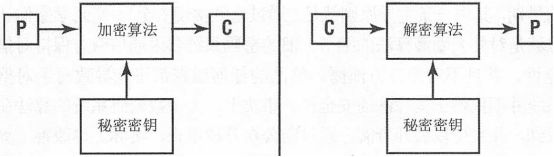
        对称密钥算法依赖于一个" 共享的秘密" 加密密钥， 该密钥会被分发给所有参与通信的成员。所有通信成员都使用这个密钥进行消息的加密和解密， 因此发送者和接收者都拥有共享密钥的副本。通信两端会使用相同的密钥加密和解密消息。当使用很长的密钥时， 对称加密难以被破解。对称密钥算法主要被用于执行批量加密， 并且只为安全服务提供机密性。对称密钥密码学也被称为秘密密钥密码学、私有密钥密码学、会话秘钥密码学、共享秘钥密码学。

        下图了对称密钥的加密和解密过程。

        对称密钥密码学具有下列几个弱点:

        密钥分发是一个主要问题。在使用对称密钥协议建立通信之前， 通信参与者必须具备一种安全交换密钥的方法。如果没有可用的安全电子通道， 那么往往必须使用离线的密钥分发方法(已不属于交换) 。

        对称密钥密码学井未实现不可否认性。由于任意通信方都可以利用共享的密钥对消息进行加密和解密， 因此无法分辨指定消息的来源。

        这种算法不可扩展。对于大的用户组来说， 使用对称密钥密码进行通信非常困难。只有在每个可能的用户组合共享私有密钥时， 组中个人之间的安全专有通信才能实现。

        密钥必须经常更新。每当有成员离开用户组时， 所有涉及这个成员的密钥都必须被抛弃。

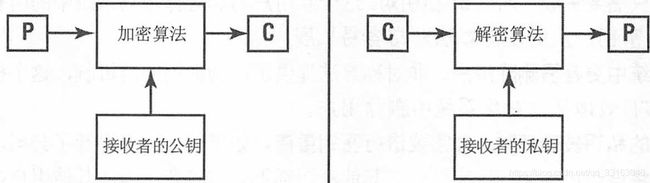
        非对称密钥算法也被称为公钥算法， 它为对称密钥加密的弱点提供了解决方案。在这个系统中，每个用户都有两个密钥: 一个在所有用户之间共享的公钥， 以及另一个只有用户自己知道并保管的私钥。但是让人意想不到的是: 相对立的和相关的密钥必须被先后应用于加密和解密。换句话说，如果使用公钥加密消息， 那么只有相关的私钥能够进行解密， 反之亦然。

        图6.4 说明了公钥密码系统中加密和解密消息、所使用的算法。

                   发送者                                                            接受者

        考虑一下这个例子: 如果Alice希望使用公钥密码学向Bob 发送消息， 她首先生成这条消息， 随后使用Bob 的公钥对消息进行加密。对这个密文进行解密的唯一可能办法是使用Bob 的私钥， 并且唯一有权使用这个密钥的用户就是Bob,因此， Alice 在加密消息后， 甚至不能对这条消息进行解密。如果Bob 希望向Alice 发出回应消息， 他会使用Ali臼的公钥对回应消息进行加密， Alice 随后可以使用她自己的私钥对消息进行解密， 从而读取这些消息。

        一旦发送者用接收者的公钥加密了消息， 那么在不知道接收者的私钥(用于生成消息的公钥/私钥对的另一半)的情况下，没有用户(包括发送者)能够解密这些信息。这就是公钥密码学的优点， 即可以使用不安全的通信通道自由共享公钥， 并在以前并不认识的用户之间创建安全的通信信道。

          RSA是使用最广泛的非对称加密算法。在现代密码学中有着极其重要的地位，如果你想选择一种有代表性的密码学算法作深入的研究，我推荐你研究RSA算法。

3数学知识基础

        RSA算法有关的数学知识总结

3.1互质关系

        如果两个正整数，除了1以外没有其他公因子，我们就称这两个数是互质关系，比如4和15

3.2 欧拉函数

        任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？比如10以内的正整数有哪几个与10互质呢？计算这个值的方法就叫做欧拉函数，以φ(n)表示，φ(10)=4。如果p,q都是质数，φ(p*q) = (p-1)(q-1)。

        举例： p=3,q=5,与15互质的数有1,2,4,7,8,11,13,14,可以数出来一共8个，同时也可以用公式计算φ(15) = (3-1)*(5-1)=8。

3.3 欧拉定理

        欧拉定理：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

        也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。

        举例：3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

3.4模反元素

        如果两个正整数e和n互质，那么一定可以找到整数d，使得 e * d - 1 被n整除，或者说e * d被n除的余数是1。这时，d就叫做e的“模反元素”。欧拉定理可以用来证明模反元素必然存在。(python: d = gmpy2.invert(e,φ(n)))

4RSA算法

        最著名的公钥密码系统以其创造者命名。1 977 年， Ronald Rivest、Adi Shamir 和Leonard Adleman提出了RSA 公钥算法， 这种算法成为今天在全世界范围仍在使用的标准。他们为这个算法申请了专利并成立了一家商业公司(RSA 安全公司)， 该公司开发使用其安全技术的主流产品。今天， RSA 算法己经构成许多知名安全基础设施(例如Microsoft、Nokia 和Cisco 公司的相应产品)的安全构架。RSA秘钥长度不固定。

4.1RSA算法计算步骤

        RSA 算法依赖于大数在因数分解时固有的计算难度。密码系统的每个用户都使用下列步骤描述的算法产生一对公钥和私钥:

（1）选择两个大的质数，计算出模数 N = p * q

（2）计算欧拉函数φ(N) = (p-1) * (q-1)，然后选择一个e(1

（3）求取e的模反数d，计算方法为:e * d ≡ 1 (mod φ)

（4）对明文m进行加密：c = m^e mod N,可以得到密文c。

（5）对密文c进行解密：m = c^d mod N,可以得到明文m。

整理：

p 和 q：两个大的质数，是另一个参数N的的两个因子。

N：大整数，可以称之为模数

e 和 d：模反数

c 和 m：密文和明文

(N, e)：公钥

(N, d)：私钥

        密钥长度：n以二进制表示的的位数，例如密钥长度为512代表n用二进制表示的长度为512bit。

验证计算：

1.假设小明想要发送的密文为m=12

2.随后小明随机选取互质的两数p=3,q=5,则n=15, φ(n)=(3-1)*(5-1)=8

3.在1~8中随机选取一个与8互质的数作为公钥e,假设小明选取了e=3,则(15， 3)为公钥

4.那么根据e *d%8=1,可以算出d=19,则(15,3)为公钥,(15,19)为私钥

5.加密时：

实际发送出去的密文为：12^3%15=3

7. 解密时：

收到密文内容为3后，解密文: 3^19%15=1162261467%15=12

4.2 RSA算法的一些疑问

问题1: 如果每个人都需要一个不同的素数，难道素数不会用完么？

答：不会，根据“素数定理”，小于n的素数的总数约为n/ln(n)。

问题2：:是否会有两个人偶然的选择了同样的素数呢？

答：很少发生。从M个素数里选出q个素数，要使至少有两个素数相同的概率达到1/2，q需要达到1.17 *M^(1/2)。

问题3：产生素数困难么？

答：不困难。查阅资料知，一般先随机产生一个奇数n,再用某种素数检测算法（如Miller-Rabin）对n进行一次性素数检测，如果n没有通过则重新生成随机数，如果n检测通过则多次重复检测，均通过则n选定为理想素数。

举例：e=3 n=7,e和n是互质的。可以找到d=5 ,使e*d-1被n整除（3*5-1被7整除）。

5 RSA常见攻击算法

5.1 模数分解

5.2 直接分解N

windows平台的RSATool

在线网站http://factordb.comhttp://factordb.com/

yafu分解

下载地址yafu download | SourceForge.net

使用cmd进入yafu的解压目录，输入yafu-x64进入命令行，最常用的命令是factor(n)，将n值分解。

D:\softwaretmp\yafu-1.34>yafu-x64
factor(111)


fac: factoring 111
fac: using pretesting plan: normal
fac: no tune info: using qs/gnfs crossover of 95 digits
div: primes less than 10000
Total factoring time = 0.0020 seconds


***factors found***

P1 = 3
P2 = 37

ans = 1

如果n很大，则可以将长值写入1.txt，末尾换行。并执行

yafu-x64 "factor(@)" -batchfile 1.txt

5.3 最大公约数

5.4 低加密指数攻击（低加密指数广播攻击）

5.5 低解密指数攻击

5.6 共模攻击

5.7

有篇博客写的还比较好读。

RSA常见攻击算法_怀念_过去的博客-CSDN博客_rsa攻击RSA算法描述 RSA算法涉及三个参数，n，e，d，私钥为n，d，公钥为n，e。 其中n是两个大素数p，q的乘积。 d是e模$ varphi(n) $的逆元，$ varphi(n) $是n的欧拉函数。 c为密文，m为明文，则加密过程如下： $ cequiv m^e mod n $ 解密过程如下：...https://blog.csdn.net/qq_24966613/article/details/84571123

6 已知x.509证书，获取私钥的步骤

6.1 从x.509中提取公钥信息。

公钥信息的格式为：

-----BEGIN PUBLIC KEY-----
MIIB*********************************************
-----END PUBLIC KEY-----

获取的方法参考以下博客的3.1章节

android apk签名文件里MANIFEST.MF、CERT.SF、CERT.RSA三者的关系_晓翔仔的博客-CSDN博客

6.2 从公钥文件提取16进制N,E

使用在线工具箱 网站The-X 在线工具箱 Base64 解码 AES RAS 解码 加密Base64,DES,AES,RSA,BASE16,Hex等常规加密/解密工具。独创数据检查技术全自动识别结果。提供精准的处理建议。https://the-x.cn/

        去除-----BEGIN PUBLIC KEY-----和-----END PUBLIC KEY-----两行后再黏贴公钥，可以获得N，e的base64编码文件。再通过反base64f方法可以获得16进制的N和e。

 

6.3 利用N和e计算私钥

        现在我们已经获得了N和e, 计算出私钥d已经存在理论上的可能了。以下代码就是可以计算私钥的代码。如果N长度较短，可以在较短的时间计算出结果。如果N长度大于512，那么我们这个方法只能给你提供学习的帮助了。

已知公钥计算私钥python代码

import random


def gcd(a, b):
    if a < b:
        a, b = b, a
    while b != 0:
        temp = a % b
        a = b
        b = temp
    return a


def getpq(n, e, d):
    p = 1
    q = 1
    while p == 1 and q == 1:
        k = d * e - 1
        g = random.randint(0, n)
        while p == 1 and q == 1 and k % 2 == 0:
            k /= 2
            y = pow(g, int(k), n)
            if y != 1 and gcd(y - 1, n) > 1:
                p = gcd(y - 1, n)
                q = n / p
    return p, q

# 分解模数n
def rsa_moder(n):
    base = 2
    while base < n:
        if n % base == 0:
            return base, n // base
        base += 1


# 求欧拉函数f(n)
def rsa_get_euler(prime1, prime2):
    return (prime1 - 1) * (prime2 - 1)


# 求私钥
def rsa_get_key(e, euler):
    k = 1
    while True:
        if (((euler * k) + 1) % e) == 0:
            return (euler * k + 1) // e
        k += 1

# 根据n,e计算d(或根据n,d计算e)
def get_rsa_e_d(n, e=None, d=None):
    if e is None and d is None:
        return

    arg = e
    if arg is None:
        arg = d

    primes = rsa_moder(n)
    p = primes[0]
    q = primes[1]

    d = rsa_get_key(arg, rsa_get_euler(p, q))

    return d

def main():
    # n = 25777
    # e = 3
    # print("input n is ",n)
    # print("input e is ",e)
    # d = get_rsa_e_d(n, e, None)
    # print("result: d is ",d)

    n = 0xBB012883****(长度2048bit,16进制长度256)
    e = 0x10001
    print("input n is ",n)
    print("input e is ",e)
    d = get_rsa_e_d(n, e, None)
    print("result: d is ",d)

    p, q = getpq(n, e, d)
    print("result: p = ", p)
    print("result: q = ", int(q))


if __name__ == '__main__':
    main()

我们用小模的公钥信息测试下代码的正确性。

D:\Users\PycharmProjects\pythonProject\venv\Scripts\python.exe D:/Users/PycharmProjects/pythonProject/main.py
input n is  25777
input e is  3
result: d is  16971
result: p =  149
result: q =  173

Process finished with exit code 0