基于蚁群算法的六轴机械臂路径规划(运动学模型建立)
机器人运动学模型的建立
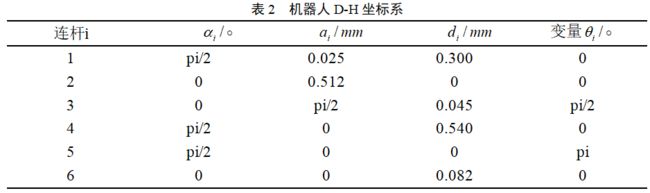
- 1 D-H参数法建立坐标系
- 2 机器人运动学分析
-
- 2.1 运动学正解
- 2.2 运动学逆解
- 3 机器人的轨迹仿真
1 D-H参数法建立坐标系
clear;
clc;
%建立机器人模型
% theta d a alpha offset
L1=Link([0 0.3 0.025 pi/2 0 ]); %定义连杆的D-H参数
L2=Link([pi/2 0 0.512 0 0 ]);
L3=Link([0 0 0.045 pi/2 0 ]);
L4=Link([0 0.504 0 pi/2 0 ]);
L5=Link([pi 0 0 pi/2 0 ]);
L6=Link([0 0.082 0 0 0 ]);
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','Mechanical arm'); %连接连杆,机器人取名manman
robot.plot([0,pi/2,0,0,pi,0]);%输出机器人模型,后面的六个角为输出时的theta姿态
robot.display();
teach(robot);
机械臂连杆之间的相对关系是通过6个4×4的变换矩阵描述,由这6个依次变换的矩阵,可以得到执行机构的坐标系和固定参考坐标系之间的变换矩阵,最后推得机器人的运动方程相邻连杆之间的D-H坐标系变换矩阵由
i i − 1 T = R o t ( Z i − 1 , θ i ) T r a n s ( 0 , 0 , d i ) T r a n s a i ( a i , 0 , 0 ) Rot ( X i , a i ) \begin{aligned} {}_{i}^{i-1}T=Rot\left( {{Z}_{i-1}},{{\theta }_{i}} \right)Trans\left( 0,0,{{d}_{i}} \right)Trans{{a}_{i}}\left( {{a}_{i}},0,0 \right)\text{Rot}\left( {{X}_{i}},{{a}_{i}} \right) \end{aligned} ii−1T=Rot(Zi−1,θi)Trans(0,0,di)Transai(ai,0,0)Rot(Xi,ai)
可以得到
i i − 1 T = [ c o s θ i − s i n θ i c o s a i s i n θ i s i n a i a i c o s θ i s i n θ i c o s θ i c o s a i − c o s θ i s i n a i a i s i n θ i 0 s i n a i c o s a i d i 0 0 0 1 ] \begin{aligned} {}_{i}^{i-1}T=\left[ \begin{matrix} cos{{\theta }_{i}} & -sin{{\theta }_{i}}cos{{a}_{i}} & sin{{\theta }_{i}}sin{{a}_{i}} & {{a}_{i}}cos{{\theta }_{i}} \\ sin{{\theta }_{i}} & cos{{\theta }_{i}}cos{{a}_{i}} & -cos{{\theta }_{i}}sin{{a}_{i}} & {{a}_{i}}sin{{\theta }_{i}} \\ 0 & sin{{a}_{i}} & cos{{a}_{i}} & {{d}_{i}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} ii−1T=⎣⎢⎢⎡cosθisinθi00−sinθicosaicosθicosaisinai0sinθisinai−cosθisinaicosai0aicosθiaisinθidi1⎦⎥⎥⎤
2 机器人运动学分析
2.1 运动学正解
1 0 T = [ c o s θ 1 0 s i n θ 1 0 s i n θ 1 0 − c o s θ 1 0 0 1 0 d 1 0 0 0 1 ] \begin{aligned} _{1}^{0}T=\left[ \begin{matrix} cos{{\theta }_{1}} & 0 & sin{{\theta }_{1}} & 0 \\ sin{{\theta }_{1}} & 0 & -cos{{\theta }_{1}} & 0 \\ 0 & 1 & 0 & {{d}_{1}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]\text{ } \end{aligned} 10T=⎣⎢⎢⎡cosθ1sinθ1000010sinθ1−cosθ10000d11⎦⎥⎥⎤ 2 1 T = [ c o s θ 2 − s i n θ 2 0 a 2 c o s θ 2 s i n θ 2 c o s θ 2 0 a 2 s i n θ 2 0 0 1 0 0 0 0 1 ] \begin{aligned} {}_{2}^{1}T=\left[ \begin{matrix} cos{{\theta }_{2}} & -sin{{\theta }_{2}} & 0 & {{a}_{2}}cos{{\theta }_{2}} \\ sin{{\theta }_{2}} & cos{{\theta }_{2}} & 0 & {{a}_{2}}sin{{\theta }_{2}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} 21T=⎣⎢⎢⎡cosθ2sinθ200−sinθ2cosθ2000010a2cosθ2a2sinθ201⎦⎥⎥⎤ 3 2 T = [ c o s θ 3 0 s i n θ 3 a 3 c o s θ 3 s i n θ 3 0 − c o s θ 3 a 3 s i n θ 3 0 1 0 0 0 0 0 1 ] \begin{aligned} {}_{3}^{2}T=\left[ \begin{matrix} cos{{\theta }_{3}} & 0 & sin{{\theta }_{3}} & {{a}_{3}}cos{{\theta }_{3}} \\ sin{{\theta }_{3}} & 0 & -cos{{\theta }_{3}} & {{a}_{3}}sin{{\theta }_{3}} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]~\text{ } \end{aligned} 32T=⎣⎢⎢⎡cosθ3sinθ3000010sinθ3−cosθ300a3cosθ3a3sinθ301⎦⎥⎥⎤ 4 3 T = [ c o s θ 4 0 − s i n θ 4 0 s i n θ 4 0 c o s θ 4 0 0 − 1 0 d 4 0 0 0 1 ] \begin{aligned} \text{ }{}_{4}^{3}T=\left[ \begin{matrix} cos{{\theta }_{4}} & 0 & -sin{{\theta }_{4}} & 0 \\ sin{{\theta }_{4}} & 0 & cos{{\theta }_{4}} & 0 \\ 0 & -1 & 0 & {{d}_{4}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} 43T=⎣⎢⎢⎡cosθ4sinθ40000−10−sinθ4cosθ40000d41⎦⎥⎥⎤ 5 4 T = [ c o s θ 5 0 − s i n θ 5 0 s i n θ 5 0 c o s θ 5 0 0 − 1 0 0 0 0 0 1 ] \begin{aligned} {}_{5}^{4}T=\left[ \begin{matrix} cos{{\theta }_{5}} & 0 & -sin{{\theta }_{5}} & 0 \\ sin{{\theta }_{5}} & 0 & cos{{\theta }_{5}} & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]\text{ } \end{aligned} 54T=⎣⎢⎢⎡cosθ5sinθ50000−10−sinθ5cosθ5000001⎦⎥⎥⎤ 6 5 T = [ c o s θ 6 − s i n θ 6 0 0 s i n θ 6 c o s θ 6 0 0 0 0 1 0 0 0 0 1 ] \begin{aligned} \text{ }{}_{6}^{5}T=\left[ \begin{matrix} cos{{\theta }_{6}} & -sin{{\theta }_{6}} & 0 & 0 \\ sin{{\theta }_{6}} & cos{{\theta }_{6}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} 65T=⎣⎢⎢⎡cosθ6sinθ600−sinθ6cosθ60000100001⎦⎥⎥⎤
对于六自由度串联机器人, a i − 1 , α i − 1 , d i , θ i {{\text{a}}_{\text{i}-1}},{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{i}-1}},{{\text{d}}_{\text{i}}},{{\text{ }\!\!\theta\!\!\text{ }}_{\text{i}}} ai−1, α i−1,di, θ i四个参数的取值可根据其下标 而得到六个不同的齐次变换矩阵 6 0 T , … , 6 5 T {}_{6}^{0}\text{T},\ldots ,{}_{6}^{5}\text{T} 60T,…,65T且有以下计算关系:
6 0 T = 6 0 T − 1 6 5 T \begin{aligned} {}_{6}^{0}T={}_{6}^{0}{{T}^{-1}}{}_{6}^{5}T \end{aligned} 60T=60T−165T
连续右乘后得到的矩阵就是机器人的正运动计算方程,将关节的变量代入方程后即可求出夹爪的空间位姿。机械臂执行机构为
6 0 T = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] \begin{aligned} {}_{6}^{0}T=\left[ \begin{matrix} {{n}_{x}} & {{o}_{x}} & {{a}_{x}} & {{p}_{x}} \\ {{n}_{y}} & {{o}_{y}} & {{a}_{y}} & {{p}_{y}} \\ {{n}_{z}} & {{o}_{z}} & {{a}_{z}} & {{p}_{z}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} 60T=⎣⎢⎢⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎥⎥⎤
其中
n x = S 6 ( C 4 S 1 − S 4 ( C 1 C 2 C 3 − C 1 S 2 S 3 ) ) + C 6 ( C 5 ( S 1 S 4 + C 4 ( C 1 C 2 C 3 − C 1 S 2 S 3 ) ) − S 5 ( C 1 C 2 S 3 + C 1 C 3 S 2 ) ) {{n}_{x}}={{S}_{6}}\left( {{C}_{4}}{{S}_{1}}-{{S}_{4}}\left( {{C}_{1}}{{C}_{2}}{{C}_{3}}-{{C}_{1}}{{S}_{2}}{{S}_{3}} \right) \right)+{{C}_{6}}\left( {{C}_{5}}\left( {{S}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{C}_{1}}{{C}_{2}}{{C}_{3}}-{{C}_{1}}{{S}_{2}}{{S}_{3}} \right) \right)-{{S}_{5}}\left( {{C}_{1}}{{C}_{2}}{{S}_{3}}+{{C}_{1}}{{C}_{3}}{{S}_{2}} \right) \right) nx=S6(C4S1−S4(C1C2C3−C1S2S3))+C6(C5(S1S4+C4(C1C2C3−C1S2S3))−S5(C1C2S3+C1C3S2))
n y = − S 6 ( C 1 C 4 − S 4 ( S 1 S 2 S 3 − C 2 C 3 S 1 ) ) − C 6 ( C 5 ( C 1 S 4 + C 4 ( S 1 S 2 S 3 − C 2 C 3 S 1 ) ) + S 5 ( C 2 S 1 S 3 + C 3 S 1 S 2 ) ) {{n}_{y}}=-{{S}_{6}}\left( {{C}_{1}}{{C}_{4}}-{{S}_{4}}\left( {{S}_{1}}{{S}_{2}}{{S}_{3}}-{{C}_{2}}{{C}_{3}}{{S}_{1}} \right) \right)-{{C}_{6}}\left( {{C}_{5}}\left( {{C}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{S}_{1}}{{S}_{2}}{{S}_{3}}-{{C}_{2}}{{C}_{3}}{{S}_{1}} \right) \right)+{{S}_{5}}\left( {{C}_{2}}{{S}_{1}}{{S}_{3}}+{{C}_{3}}{{S}_{1}}{{S}_{2}} \right) \right) ny=−S6(C1C4−S4(S1S2S3−C2C3S1))−C6(C5(C1S4+C4(S1S2S3−C2C3S1))+S5(C2S1S3+C3S1S2))
n z = C 6 ( S 5 ( C 2 C 3 − S 2 S 3 ) + C 4 C 5 ( C 2 S 3 + C 3 S 2 ) − S 4 S 6 ( C 2 S 3 + C 3 S 2 ) ) {{n}_{z}}={{C}_{6}}\left( {{S}_{5}}\left( {{C}_{2}}{{C}_{3}}-{{S}_{2}}{{S}_{3}} \right)+{{C}_{4}}{{C}_{5}}\left( {{C}_{2}}{{S}_{3}}+{{C}_{3}}{{S}_{2}} \right)-{{S}_{4}}{{S}_{6}}\left( {{C}_{2}}{{S}_{3}}+{{C}_{3}}{{S}_{2}} \right) \right) nz=C6(S5(C2C3−S2S3)+C4C5(C2S3+C3S2)−S4S6(C2S3+C3S2))
o x = C 6 ( C 4 S 2 − S 4 ( C 1 C 2 C 3 − C 1 S 2 S 3 ) ) − S 6 ( C 5 ( S 1 S 4 + C 4 ( C 1 C 2 C 3 − C 1 S 2 S 3 ) ) − S 5 ( C 1 C 2 S 3 + C 1 C 3 S 2 ) ) {{o}_{x}}={{C}_{6}}\left( {{C}_{4}}{{S}_{2}}-{{S}_{4}}\left( {{C}_{1}}{{C}_{2}}{{C}_{3}}-{{C}_{1}}{{S}_{2}}{{S}_{3}} \right) \right)-{{S}_{6}}\left( {{C}_{5}}\left( {{S}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{C}_{1}}{{C}_{2}}{{C}_{3}}-{{C}_{1}}{{S}_{2}}{{S}_{3}} \right) \right)-{{S}_{5}}\left( {{C}_{1}}{{C}_{2}}{{S}_{3}}+{{C}_{1}}{{C}_{3}}{{S}_{2}} \right) \right) ox=C6(C4S2−S4(C1C2C3−C1S2S3))−S6(C5(S1S4+C4(C1C2C3−C1S2S3))−S5(C1C2S3+C1C3S2))
o y = S 6 ( C 5 ( C 1 S 4 + C 4 ( S 1 S 2 S 3 − C 2 C 3 S 1 ) ) + S 5 ( C 2 S 1 S 3 + C 3 S 1 S 2 ) ) − C 6 ( C 1 C 4 − S 4 ( S 1 S 2 S 3 − C 2 C 3 S 1 ) ) {{o}_{y}}={{S}_{6}}\left( {{C}_{5}}\left( {{C}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{S}_{1}}{{S}_{2}}{{S}_{3}}-{{C}_{2}}{{C}_{3}}{{S}_{1}} \right) \right)+{{S}_{5}}\left( {{C}_{2}}{{S}_{1}}{{S}_{3}}+{{C}_{3}}{{S}_{1}}{{S}_{2}} \right) \right)-{{C}_{6}}\left( {{C}_{1}}{{C}_{4}}-{{S}_{4}}\left( {{S}_{1}}{{S}_{2}}{{S}_{3}}-{{C}_{2}}{{C}_{3}}{{S}_{1}} \right) \right) oy=S6(C5(C1S4+C4(S1S2S3−C2C3S1))+S5(C2S1S3+C3S1S2))−C6(C1C4−S4(S1S2S3−C2C3S1))
o z = − S 6 ( S 5 ( C 2 C 3 − S 2 S 3 ) + C 4 C 5 ( C 2 S 3 + C 3 S 2 ) ) − C 6 S 4 ( C 2 S 3 + C 3 S 2 ) {{o}_{z}}=-{{S}_{6}}\left( {{S}_{5}}\left( {{C}_{2}}{{C}_{3}}-{{S}_{2}}{{S}_{3}} \right)+{{C}_{4}}{{C}_{5}}\left( {{C}_{2}}{{S}_{3}}+{{C}_{3}}{{S}_{2}} \right) \right)-{{C}_{6}}{{S}_{4}}\left( {{C}_{2}}{{S}_{3}}+{{C}_{3}}{{S}_{2}} \right) oz=−S6(S5(C2C3−S2S3)+C4C5(C2S3+C3S2))−C6S4(C2S3+C3S2)
a x = S 5 ( S 1 S 4 + C 4 ( C 1 C 2 C 3 − C 1 S 2 S 3 ) + C 5 ( C 1 C 2 S 3 + C 1 C 3 S 2 ) ) {{a}_{x}}={{S}_{5}}\left( {{S}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{C}_{1}}{{C}_{2}}{{C}_{3}}-{{C}_{1}}{{S}_{2}}{{S}_{3}} \right)+{{C}_{5}}\left( {{C}_{1}}{{C}_{2}}{{S}_{3}}+{{C}_{1}}{{C}_{3}}{{S}_{2}} \right) \right) ax=S5(S1S4+C4(C1C2C3−C1S2S3)+C5(C1C2S3+C1C3S2))
a y = C 5 ( C 2 S 1 S 3 + C 3 S 1 S 2 − S 5 ( C 1 S 4 + C 4 ( S 1 S 2 S 3 − C 2 C 3 S 1 ) ) {{a}_{y}}={{C}_{5}}\left( {{C}_{2}}{{S}_{1}}{{S}_{3}}+{{C}_{3}}{{S}_{1}}{{S}_{2}}-{{S}_{5}}\left( {{C}_{1}}{{S}_{4}}+{{C}_{4}}\left( {{S}_{1}}{{S}_{2}}{{S}_{3}}-{{C}_{2}}{{C}_{3}}{{S}_{1}} \right) \right) \right. ay=C5(C2S1S3+C3S1S2−S5(C1S4+C4(S1S2S3−C2C3S1))
a z = C 4 S 5 ( C 2 S 3 + C 3 S 2 ) − C 5 ( C 2 C 3 − S 2 S 3 ) {{a}_{z}}={{C}_{4}}{{S}_{5}}\left( {{C}_{2}}{{S}_{3}}+{{C}_{3}}{{S}_{2}} \right)-{{C}_{5}}\left( {{C}_{2}}{{C}_{3}}-{{S}_{2}}{{S}_{3}} \right) az=C4S5(C2S3+C3S2)−C5(C2C3−S2S3)
p x = d 4 ( C 1 C 2 S 3 + C 1 C 3 S 2 ) + a 2 C 1 C 2 + a 3 C 1 C 2 C 3 − a 3 C 1 S 2 S 3 {{p}_{x}}={{d}_{4}}\left( {{C}_{1}}{{C}_{2}}{{S}_{3}}+{{C}_{1}}{{C}_{3}}{{S}_{2}} \right)+{{a}_{2}}{{C}_{1}}{{C}_{2}}+{{a}_{3}}{{C}_{1}}{{C}_{2}}{{C}_{3}}-{{a}_{3}}{{C}_{1}}{{S}_{2}}{{S}_{3}} px=d4(C1C2S3+C1C3S2)+a2C1C2+a3C1C2C3−a3C1S2S3
p y = d 4 ( C 2 S 1 S 3 + C 3 S 1 S 2 ) + a 2 C 2 S 1 + a 3 C 2 C 3 S 1 − a 3 S 1 S 2 S 3 {{p}_{y}}={{d}_{4}}\left( {{C}_{2}}{{S}_{1}}{{S}_{3}}+{{C}_{3}}{{S}_{1}}{{S}_{2}} \right)+{{a}_{2}}{{C}_{2}}{{S}_{1}}+{{a}_{3}}{{C}_{2}}{{C}_{3}}{{S}_{1}}-{{a}_{3}}{{S}_{1}}{{S}_{2}}{{S}_{3}} py=d4(C2S1S3+C3S1S2)+a2C2S1+a3C2C3S1−a3S1S2S3
p z = a 2 S 2 − d 4 ( C 2 C 3 − S 2 S 3 ) + a 3 C 2 S 3 + a 3 C 3 S 2 {{p}_{z}}={{a}_{2}}{{S}_{2}}-{{d}_{4}}\left( {{C}_{2}}{{C}_{3}}-{{S}_{2}}{{S}_{3}} \right)+{{a}_{3}}{{C}_{2}}{{S}_{3}}+{{a}_{3}}{{C}_{3}}{{S}_{2}} pz=a2S2−d4(C2C3−S2S3)+a3C2S3+a3C3S2
代码如下:
theta=[0.0351121605635749 -0.729064371146205 -0.531988015514109 0 -1.88054026692948 3.10648049302622];%指定的关节角
p=robot.fkine(theta);%fkine正解函数,根据我们给定的关节角theta,求解出末端位姿p
2.2 运动学逆解
在2.1节建立了六轴机器人的正运动学方程,给定各个关节的旋转角度就可以求出末端的位姿。然而在实际操作的过程中,情况恰恰相反。我们通常需要在知道末端位姿的情况下求出各个关节旋转角度,这就是机器人反向运动学的问题,也称为求运动学逆解,即由笛卡尔空间到关节空间的变换。
针对机器人求逆解的问题,求解方法多种多样,其中应用最广的是封闭解法,因为求封闭解计算速度快、效率高、便于实时控制。封闭解法包括两种方法:一种是代数解法,另一种是几何解法。目前已建立的一种系统化的代数解法为:运用变换矩阵就可得出一个可求解的三角函数方程式。重复上述过程,直到求解出所有的未知数。
六轴机器人运动学方程可以写为:
6 0 T = 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 T = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] \begin{aligned} {}_{6}^{0}T={}_{1}^{0}T{}_{2}^{1}T{}_{3}^{2}T{}_{4}^{3}T{}_{5}^{4}T{}_{6}^{5}T=\left[ \begin{matrix} {{n}_{x}} & {{o}_{x}} & {{a}_{x}} & {{p}_{x}} \\ {{n}_{y}} & {{o}_{y}} & {{a}_{y}} & {{p}_{y}} \\ {{n}_{z}} & {{o}_{z}} & {{a}_{z}} & {{p}_{z}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \end{aligned} 60T=10T21T32T43T54T65T=⎣⎢⎢⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎥⎥⎤
在该运动学方程中,等式左边的矩阵中的元素 n x , n y , n z , o x , o y , o z , a x , a y , a z , p x , p y , p z {{\text{n}}_{\text{x}}},{{\text{n}}_{\text{y}}},{{\text{n}}_{\text{z}}},{{\text{o}}_{\text{x}}},{{\text{o}}_{\text{y}}},{{\text{o}}_{\text{z}}},{{\text{a}}_{\text{x}}},{{\text{a}}_{\text{y}}},{{\text{a}}_{\text{z}}},{{\text{p}}_{\text{x}}},{{\text{p}}_{\text{y}}},{{\text{p}}_{\text{z}}} nx,ny,nz,ox,oy,oz,ax,ay,az,px,py,pz均为已知的,而等式右边的6个矩阵是未知的,它们的值取决于关节变量 θ 1 , … , θ 6 {{\text{ }\!\!\theta\!\!\text{ }}_{1}},\ldots ,{{\text{ }\!\!\theta\!\!\text{ }}_{6}} θ 1,…, θ 6的大小。用未知的连杆的逆变换左乘方程的两端,把关节变量分离出来,从而求出解,按照这种方法让矩阵左右两边的元素相等便可求出各个关节变量的值。
6 5 T − 1 T = 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T \begin{aligned} {}_{6}^{5}{{T}^{-1}}T={}_{1}^{0}T{}_{2}^{1}T{}_{3}^{2}T{}_{4}^{3}T{}_{5}^{4}T \end{aligned} 65T−1T=10T21T32T43T54T 5 4 T − 1 6 5 T − 1 T = 1 0 T 2 1 T 3 2 T 4 3 T \begin{aligned} {}_{5}^{4}{{T}^{-1}}{}_{6}^{5}{{T}^{-1}}T={}_{1}^{0}T{}_{2}^{1}T{}_{3}^{2}T{}_{4}^{3}T \end{aligned} 54T−165T−1T=10T21T32T43T 4 3 T − 1 5 4 T − 1 6 5 T − 1 T = 1 0 T 2 1 T 3 2 T \begin{aligned} {}_{4}^{3}{{T}^{-1}}{}_{5}^{4}{{T}^{-1}}{}_{6}^{5}{{T}^{-1}}T={}_{1}^{0}T{}_{2}^{1}T{}_{3}^{2}T \end{aligned} 43T−154T−165T−1T=10T21T32T 3 2 T − 1 4 3 T − 1 5 4 T − 1 6 5 T − 1 T = 1 0 T \begin{aligned} {}_{3}^{2}{{T}^{-1}}{}_{4}^{3}{{T}^{-1}}{}_{5}^{4}{{T}^{-1}}{}_{6}^{5}{{T}^{-1}}T={}_{1}^{0}T \end{aligned} 32T−143T−154T−165T−1T=10T
代码:
T1=transl(452.120,149.090,-432.450);%根据给定起始点,得到起始点位姿
T2=transl(514.1,-155.5,-136);%根据给定终止点,得到终止点位姿
q1=robot.ikine(T1);%根据起始点位姿,得到起始点关节角
q2=robot.ikine(T2);%根据终止点位姿,得到终止点关节角
3 机器人的轨迹仿真
为了更好地验证机器人数学模型的正确性以及方便地进行带控制参数的运动仿真,本文基于Robotics Toolbox for MATLAB工具箱,对所建立的六自由度机器人数学模型进行验证。主要代码如下:
利用Link指令,可以将机器人的六个轴的参数一一指定。利用display指令,可以在command window处检查输入的D-H模型是否正确。利用teach指令,可以得到机器人的棍棒模型,如图2所示。

对于机器人的运动控制来说,常用的轨迹规划方式是点到点模式,本文选取了一个抬手臂的动作,对夹爪的位姿进行轨迹规划。
利用jtraj指令,可以将两点间的轨迹用一条五阶多项式曲线逼近,以确保机器人在运动过程中的平滑性,图3为机械臂的运动轨迹。利用plot指令,可以将规划的轨迹用动画仿真的形式展现,图4为机械臂的棍棒运动模型。
代码:
T1=transl(0.5,0.2,0);%根据给定起始点,得到起始点位姿
T2=transl(0.5,-0.2,0.9);%根据给定终止点,得到终止点位姿
q1=robot.ikine(T1);%根据起始点位姿,得到起始点关节角
q2=robot.ikine(T2);%根据终止点位姿,得到终止点关节角
[q ,qd, qdd]=jtraj(q1,q2,50); %五次多项式轨迹,得到关节角度,角速度,角加速度,50为采样点个数
grid on
T = robot.fkine(q);%根据插值,得到末端执行器位姿 (正向运动学,为了画出末端轨迹)
t = [];
for i=1:50
[R_temp, t_temp] = tr2rt(T(i));
t = [t t_temp];
end
plot3(t(1, :), t(2, :), t(3, :), 'linewidth', 3);%输出末端轨迹
hold on
% while(1)
% robot.plot(q);%动画演示
% end
robot.plot(q);%动画演示
figure(2)
i=1:4;
subplot(2,2,1);
plot(q(:,i));
title('位置');
grid on;
subplot(2,2,2);
i=1:4;
plot(qd(:,i));
title('速度');
grid on;
subplot(2,2,3);
i=1:4;
plot(qdd(:,i));
title('加速度');
grid on;
Tc=ctraj(T1,T2,50);%利用匀加速匀减速规划轨迹
Tjtraj=transl(Tc);
subplot(2,2,4);
plot2(Tjtraj,'r');
title('p1到p2直线轨迹');