代码随想录算法训练营第七天| 454. 四数相加II，383. 赎金信，15. 三数之和，18. 四数之和，哈希表总结

454.四数相加II

建议：本题是使用Map巧妙解决的问题，好好体会一下哈希法如何提高程序执行效率，降低时间复杂度，当然使用哈希法会提高空间复杂度，但一般来说我们都是舍空间换时间， 工业开发也是这样。

题目链接/文章讲解/视频讲解：代码随想录

重点：

1. 因为要存储前两个数组的不同下标和的键值对 sum: count，后两个数组需要查找这个键值对，所以我们用Map的哈希表

思路：

1. 先把前两个数组的不同下标的和用Map记录下来，然后用0 - 后两个数组的和来对Map进行查找，找到了就加上Map的value值

public static int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        // 计算有多少组下标对应的数字的和为0
        int result = 0;
        // 存放前两个数组的 sum: count
        Map records = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                int sum = nums1[i] + nums2[j];
                records.put(sum, records.getOrDefault(sum, 0) + 1);
            }
        }
        // 用后两个数组的和的负数来在records中查找是否有匹配的
        // 找到了result += count
        for (int i = 0; i < nums3.length; i++) {
            for (int j = 0; j < nums4.length; j++) {
                int sum = nums3[i] + nums4[j];
                if (records.containsKey(-sum)) {
                    result += records.get(-sum);
                }
            }
        }
        return result;
}

383. 赎金信

建议：本题和242. 有效的字母异位词是一个思路 ，算是拓展题

题目链接/文章讲解： 代码随想录

重点：

1. 因为只有26个字母，所以使用数组来当哈希表结构

思路;

1. 把magazine中出现的每个字符的次数存放到数组中

2. 把ransomNote中出现的每个字符在对应的index上 --

3. 期间如果有某个index的值小于0，说明magazine的字符无法组成ransomNote

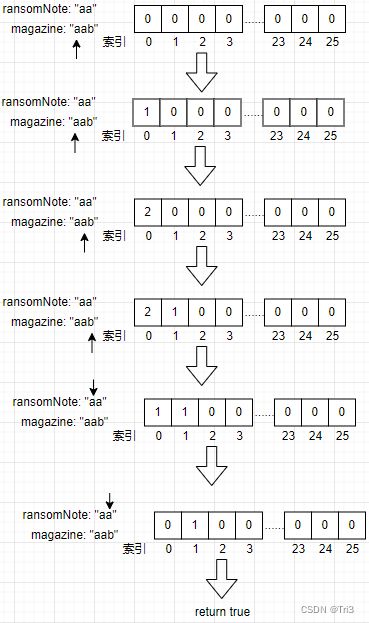
public static boolean canConstruct(String ransomNote, String magazine) {
        int[] magazineCount = new int[26];
        // 把magazine的字符出现的次数存放进数组
        for (int i = 0; i < magazine.length(); i++) {
            magazineCount[magazine.charAt(i) - 'a']++;
        }
        // 把ransomNote中出现的字符的对应的数组的值减1
        // 期间如果有某个值小于0，说明magazine中的字符无法满足ransomNote的组成
        for (int i = 0; i < ransomNote.length(); i++) {
            int temp = --magazineCount[ransomNote.charAt(i) - 'a'];
            if (temp < 0) {
                return false;
            }
        }
        return true;
}

15. 三数之和

建议：本题虽然和两数之和很像，也能用哈希法，但用哈希法会很麻烦，双指针法才是正解，可以先看视频理解一下双指针法的思路，文章中讲解的，哈希法很麻烦。

题目链接/文章讲解/视频讲解： 代码随想录

重点：

1. 双指针法

思路：

1. 双指针法

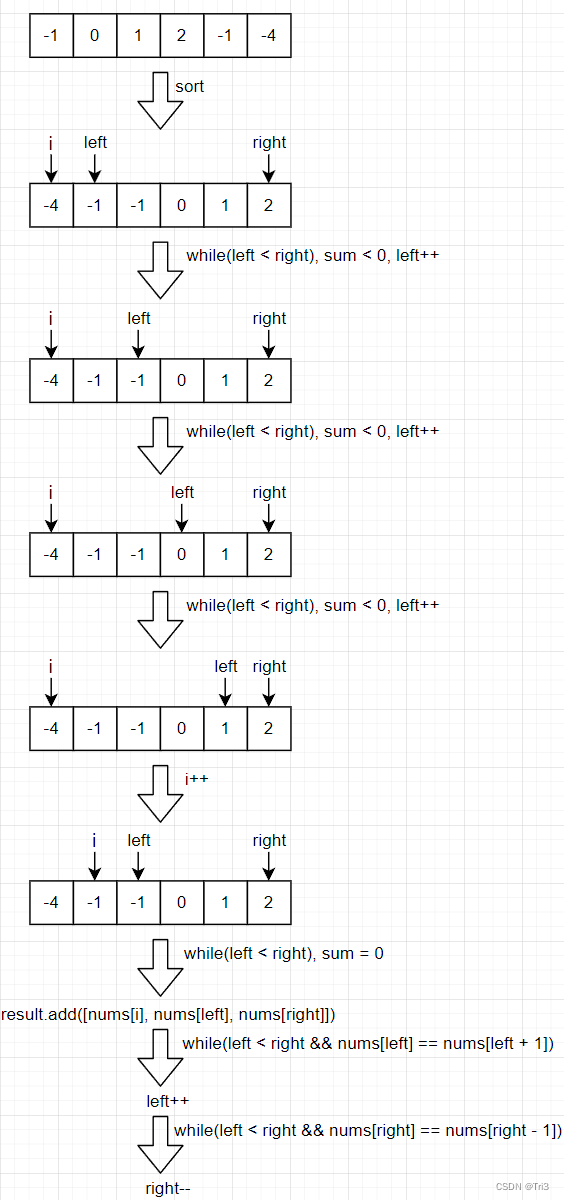
(1) 先把数组从小到大排序

(2) 从头开始遍历排序好的数组，如果i = i - 1，直接continue对 i 进行去重，并定义一个left = i + 1， right = nums.length - 1

(3) 不断的移动left和right，当i + left + right小于0时说明sum太小了，需要变大，因为是排序好的数组，直接把left++就可以把left移动到更大的数去了

(4) 不断的移动left和right，当i + left + right大于0时说明sum太大了，需要变小，因为是排序好的数组，直接把right--就可以把right移动到更小的数去了

(5) 当i + left + right等于0时，把这三个值存放到result中，接下来要对left和right分别去重。如果left = left + 1， left++。如果right = right - 1，right--

public static List> threeSum(int[] nums) {
        // 先把数组从小到大排序
        Arrays.sort(nums);
        List> result = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            // 如果i所指的数都已经大于0了，后面的数又都比它大，直接return
            if (nums[i] > 0) {
                return result;
            }
            // 如果i所指的数和它前面的数相等，说明这个数已经被判断过了，continue
            if (i >= 1 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 两个指针，一个指i + 1，一个指数组末尾
            int left = i + 1;
            int right = nums.length - 1;
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum > 0) {
                    // 当三数之和大于0时，证明需要减小，把right往前移一个
                    right--;
                } else if (sum < 0) {
                    // 当三数之和小于0时，证明需要变大，把left往后移一个
                    left++;
                } else {
                    // 当三数之和等于0时，需要对left和right所指的数分别去重
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    while (left < right && nums[left + 1] == nums[left]) {
                        left++;
                    }
                    while (left < right && nums[right - 1] == nums[right]) {
                        right--;
                    }
                    // 为什么同时移动两个指针？
                    // 因为如果只移动了right，你前面两数i和left都已经固定了，
                    // 为了三数和为0，你right也相当于是固定的，
                    // 也就是说i和left都已经判断过了，right也相当于判断过了。
                    // 所以当上面的去重操作完成之后，left和right肯定同时移动的
                    left++;
                    right--;
                }
            }
        }
        return result;
}

18. 四数之和

建议： 要比较一下，本题和454. 四数相加II 的区别，为什么454.四数相加II 会简单很多，这个想明白了，对本题理解就深刻了。 本题思路整体和三数之和一样的，都是双指针，但写的时候有很多小细节，需要注意，建议先看视频。 

题目链接/文章讲解/视频讲解：代码随想录

重点：

1. 双指针法

思路：

1. 双指针法

(1) 先把数组从小到大排序

(2) 两个for循环，第一个for循环 i 从头开始，第二个for循环从上一个循环 i + 1 开始

(3) 不断的移动left和right，当i + j + left + right小于0时说明sum太小了，需要变大，因为是排序好的数组，直接把left++就可以把left移动到更大的数去了

(4) 不断的移动left和right，当i + j + left + right大于0时说明sum太大了，需要变小，因为是排序好的数组，直接把right--就可以把right移动到更小的数去了

(5) 当i + j + left + right等于0时，把这四个值存放到result中，接下来要对left和right分别去重。如果left = left + 1， left++。如果right = right - 1，right--

(6) 把 j 移动到下一个，接着判断

public static List> fourSum(int[] nums, int target) {
        List> result = new ArrayList<>();
        // 先从小到大排序数组
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 1; i++) {
            // 如果nums[i]已经大于target了，并且nums[i]已经大于0
            // nums[i]已经大于0说明后面的数肯定也都大于0，直接返回
            if (nums[i] > target && nums[i] > 0) {
                return result;
            }
            // 如果当前nums[i]和前一个数一样，跳过
            if (i >= 1 && nums[i] == nums[i - 1]) {
                continue;
            }
            for (int j = i + 1; j < nums.length; j++) {
                // 如果i和j已经相差两个，并且nums[j]和前一个数一样，跳过
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                // 两个指针，一个指j + 1，一个指数组末尾
                int left = j + 1;
                int right = nums.length - 1;
                while (left < right) {
                    long sum = (long)nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum > target) {
                        // 当四数之和大于target时，证明需要减小，把right往前移一个
                        right--;
                    } else if (sum < target) {
                        // 当四数之和小于target时，证明需要变大，把left往后移一个
                        left++;
                    } else {
                        // 当四数之和等于target时，需要对left和right所指的数分别去重
                        result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        while (left < right && nums[left + 1] == nums[left]) {
                            left++;
                        }
                        while (left < right && nums[right - 1] == nums[right]) {
                            right--;
                        }
                        left++;
                        right--;
                    }
                }
            }
        }
        return result;
}

哈希表总结

哈希表理论知识

一般来说哈希表都是用来快速判断一个元素是否出现集合里。

对于哈希表，要知道哈希函数和哈希碰撞在哈希表中的作用：

• 哈希函数是把传入的key映射到符号表的索引上。
• 哈希碰撞处理有多个key映射到相同索引上时的情景，处理碰撞的普遍方式是拉链法和线性探测法。

接下来是常见的三种哈希结构：

• 数组
• set（集合）
• map（映射）

哈希经典题目

数组作为哈希表

一些应用场景就是为数组量身定做的。

在242.有效的字母异位词 (opens new window)中，我们提到了数组就是简单的哈希表，但是数组的大小是受限的！这道题目包含小写字母，那么使用数组来做哈希最合适不过。

在383.赎金信 (opens new window)中同样要求只有小写字母，那么就给我们浓浓的暗示，用数组！

一些同学可能想，用数组干啥，都用map不就完事了。

上面两道题目用map确实可以，但使用map的空间消耗要比数组大一些，因为map要维护红黑树或者符号表，而且还要做哈希函数的运算。所以数组更加简单直接有效！

set作为哈希表

在349. 两个数组的交集 (opens new window)中我们给出了什么时候用数组就不行了，需要用set。这道题目没有限制数值的大小，就无法使用数组来做哈希表了。

主要因为如下两点：

• 数组的大小是有限的，受到系统栈空间（不是数据结构的栈）的限制。
• 如果数组空间够大，但哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

所以此时一样的做映射的话，就可以使用set了。

map作为哈希表

在1.两数之和 (opens new window)中map正式登场。

来说一说，使用数组和set来做哈希法的局限：

• 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
• set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x和y的下标。所以set也不能用。

map是一种的结构，本题可以用key保存数值，用value在保存数值所在的下标。所以使用map最为合适。

在454.四数相加 (opens new window)中我们提到了其实需要哈希的地方都能找到map的身影。

本题咋眼一看好像和18. 四数之和 (opens new window)，15.三数之和 (opens new window)差不多，其实差很多！

关键差别是本题为四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑重复问题，而18. 四数之和 (opens new window)，15.三数之和 (opens new window)是一个数组（集合）里找到和为0的组合，可就难很多了！

所以18. 四数之和，15.三数之和都推荐使用双指针法！

总结

对于哈希表的知识相信很多同学都知道，但是没有成体系。

本篇我们从哈希表的理论基础到数组、set和map的经典应用，把哈希表的整个全貌完整的呈现给大家。

同时也强调虽然map是万能的，详细介绍了什么时候用数组，什么时候用set。

相信通过这个总结篇，大家可以对哈希表有一个全面的了解。