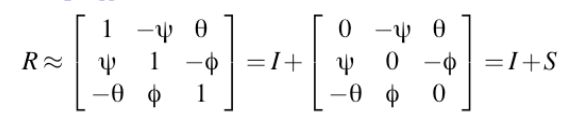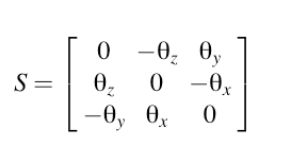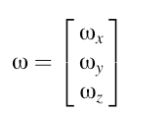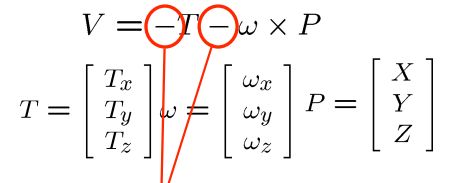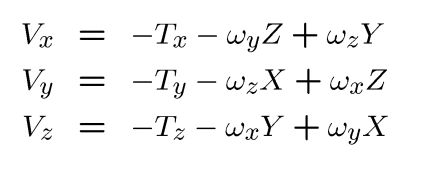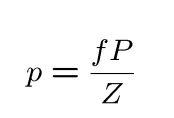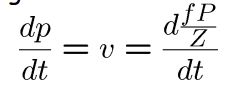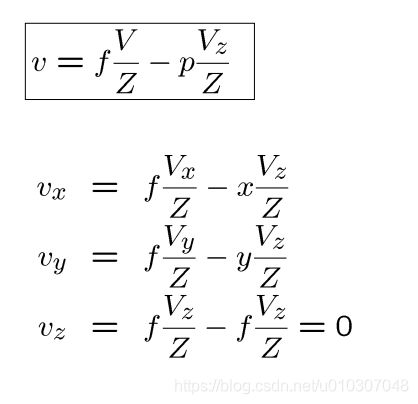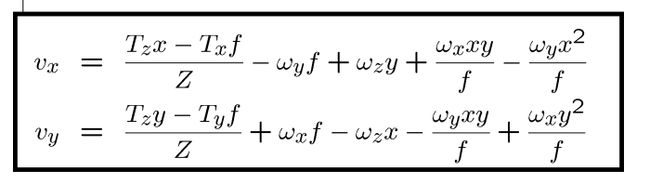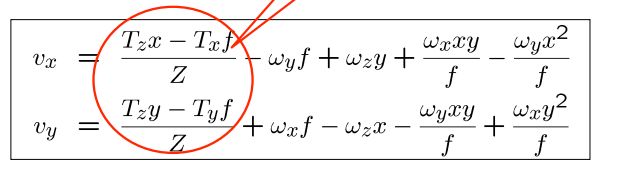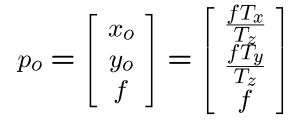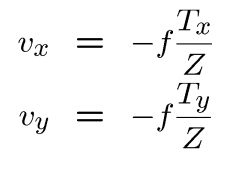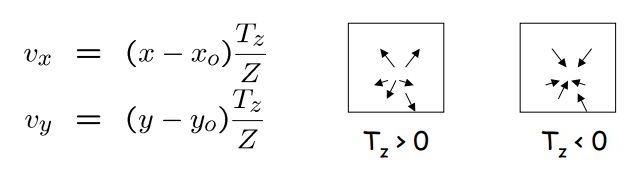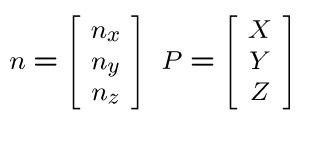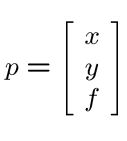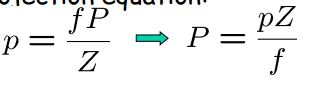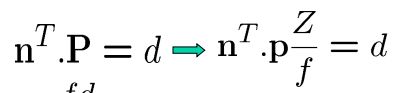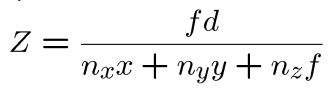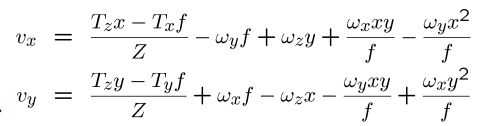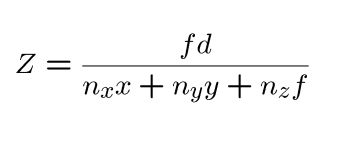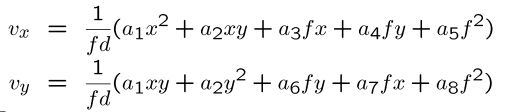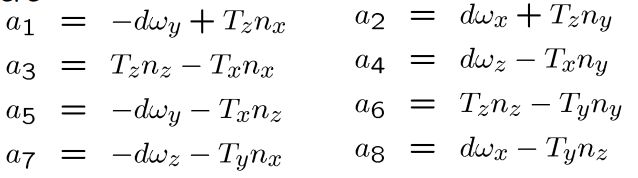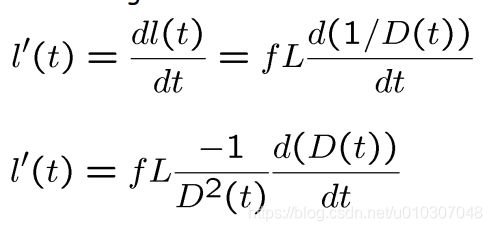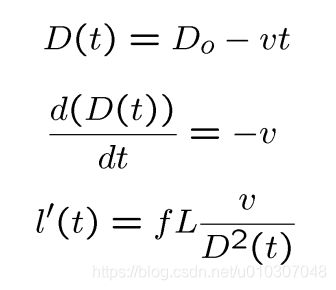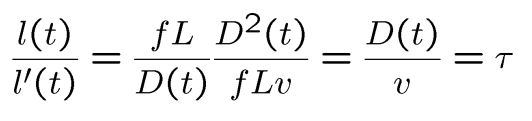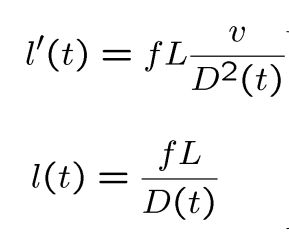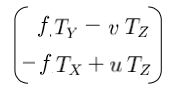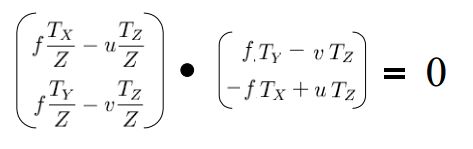【计算机视觉】Lecture 22：相机运动
移动的相机
相机拍摄由时间t索引的图像（帧）序列
从一个时间到下一个时间，相机经历旋转（滚转、俯仰、偏航）和平移（tx、ty、tz）
运动（位移）场
运动场Motion Field和光流Optic Flow
运动场：三维相对速度矢量在二维图像平面上的投影
光流：在图像中观察到的亮度模式（brightness patterns）的二维位移
运动场是我们想知道的。
光流是我们可以估计的。
有时光流是对未知运动流的一个很好的近似。
然后我们可以推断相机和世界中的物体之间的相对运动。
注意：光流不等于运动场
考虑一个移动的光源：
MF=0，因为场景中的点没有移动
OF不等于0，因为图像中存在移动模式
运动场
我们将推导一个三维场景结构和速度与二维运动流场的关系方程。
什么是场field？
在空间中的每个点上绘制一个向量。这是一个向量场。在三维空间中，我们将研究由相机运动引起的三维速度矢量场。
在二维中，我们将看到三维速度矢量在图像中的投影。图像中的每个点都有一个二维流矢量。这是二维运动流场。
回忆：一般的投影方程
策略：
- 假设内参已知（设置为I）
- 时间 t 时，设 R = I，T = 0
- 时间 t + 1 时，运动产生相对的 R 和 T（简化假设：小运动–>小旋转）
- 计算三维速度向量
- 计算二维速度向量（X，Y，Z，R，T，f 的函数）
三维世界点的位移
时间 t：三维世界点 P
时间 t + 1：三维世界点 RP + T
三维位移 = RP + T - P
现在考虑短时间段（比如两个视频帧之间的时间=1/30秒）。可以假设在那个时间段内有一个小的旋转角度。进行小角度近似并重写位移。在极限（无穷小的时间周期）中，我们会得到一个速度。
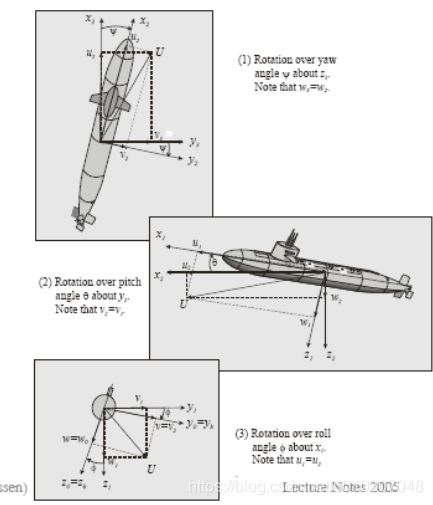
用欧拉角写出旋转矩阵
欧拉角变换
三个主旋转
线性速度变换（zyx转换—rpy）
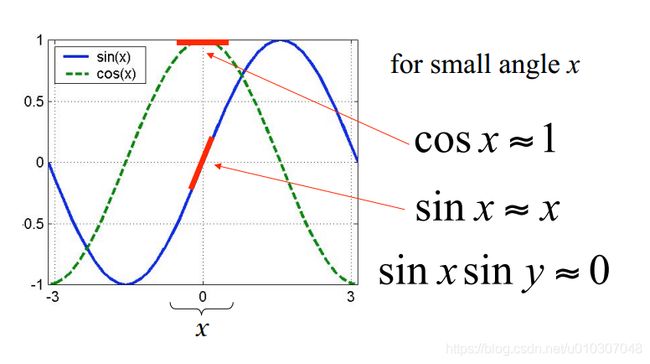
小角度近似
三维速度
在小角度近似下，位移 = RP + T - P = (I + S)P + T - P = SP + T
其中，
注意：
时间 t 取极限情况下，位移变成速度
其中 
三维相对速度
关于相机点 P 的相对速度
•我们刚刚推导了一个方程，将R，T和每个场景点（相机坐标系下）的三维速度矢量联系起来。
•我们可以把速度看作场景中的一个小矢量。
•现在问一下，这个向量在图像中的投影是什么样子的？它是一个二维向量。它是构成运动场的矢量之一！
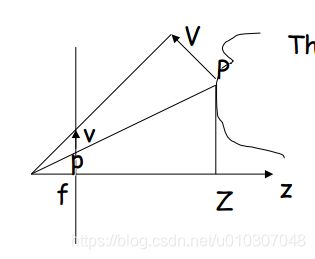
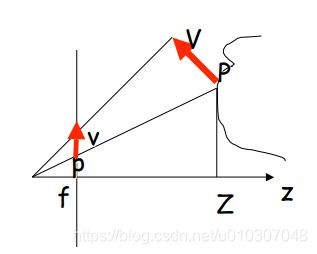
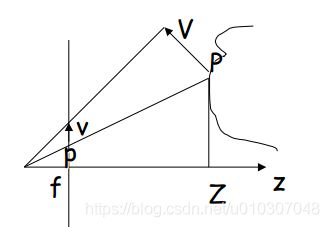
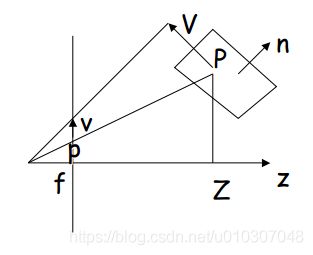
运动场：p 的二维速度
透视投影
上式对时间求导
以上红圈为平移部分
以上红圈为旋转部分
注意：旋转分量与深度Z无关！
特例1：纯平移
假设 Tz 不等于 0
定义：
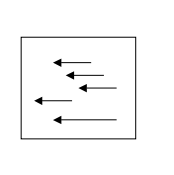
假如 Tz = 0 则
所有运动场矢量彼此平行，并且与深度成反比！（与简单的立体视觉联系起来）
此情况下的运动场是径向的：
- 它由通过 po=（xo，yo）的向量组成
- 假如：
1）Tz > 0 (相机向物体移动)
向量远离po
po是扩展点 POINT OF EXPANSION
2）Tz < 0 (相机远离物体)
向量指向po
po是收缩点 POINT OF CONTRACTION
纯旋转：运动场的性质
假如 Tz 不等于0，则运动场是径向的，所有向量都指向（或远离）单个点po。如果Tz＝0，则运动场是平行的。
运动场向量的长度与深度Z成反比。如果Tz≠0，它也与p和po之间的距离成正比
po是平移方向的灭点（vanishing point）
po是平行于平移向量的光线与图像平面的交点
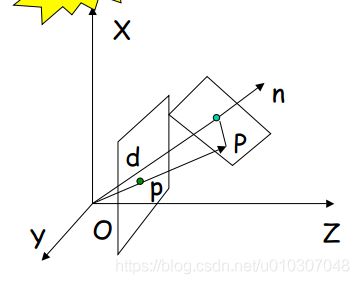
特例2：移动平面
问题：移动平面的运动场是什么样子的？
平面上的点必须满足描述平面的方程
其中
n 是垂直于平面的单位向量
d 是从平面到原点的距离
注意：如果平面是在相机坐标系下移动，则 n 和 d 是时间的函数
令 
成为 P 的成像点
使用小孔投影方程：
使用平面方程：
解出Z ：
考虑运动场方程
将 Z 
代入，则运动场方程变为：
运动场向量由低阶（二次）多项式给出。
•他们的系数。a1到a8（仅8个！）是 n，d，T 和 ω 的函数。
•也就是说，可以估计 8 个参数的全局流flow，而不是每个像素2个参数！大大节省了时间和增强了鲁棒性。
应用：碰撞时间
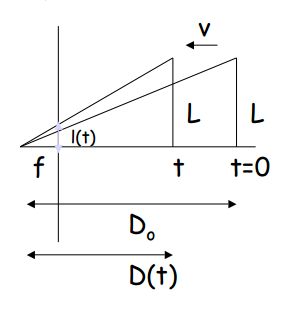
高度 L 的物体以恒定速度v移动：
时间 t = 0 时，物体在：D(0) = Do
时间 t 时，物体在：D(t) = Do - vt
它将在以下时间撞向相机：D(τ) = Do – vτ = 0，τ = Do/v
物体在成像平面上的大小为 l(t)
上式对时间求导
比例为：
上两式可以直接从成像平面上测量得到
碰撞时间：
不需要知道 L, Do, v，就可以计算碰撞时间
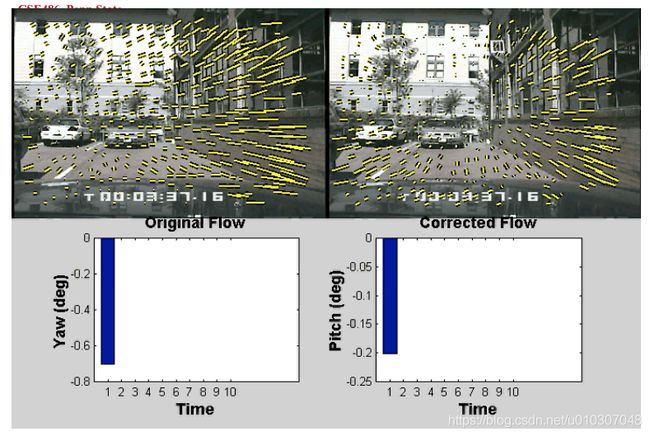
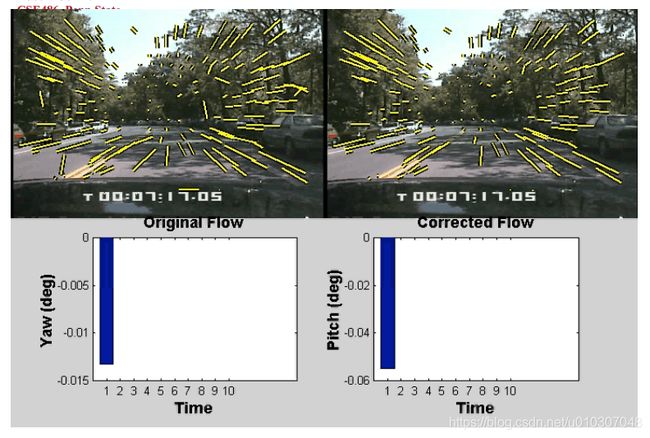
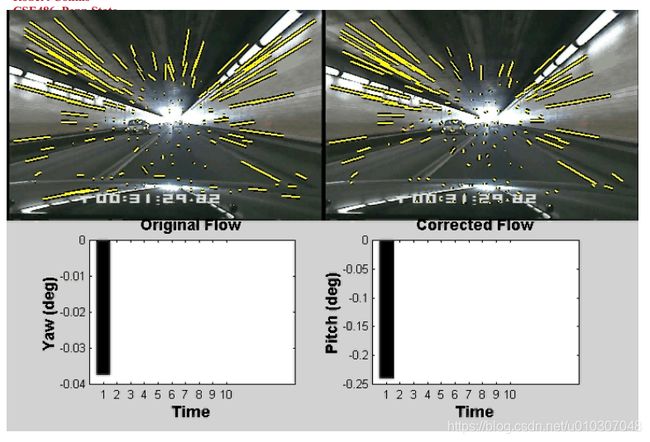
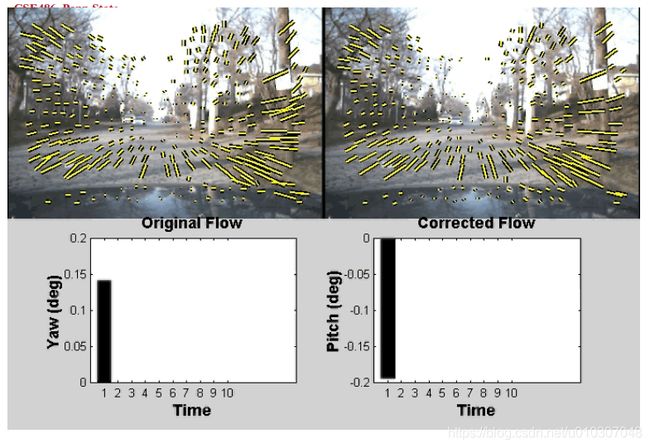
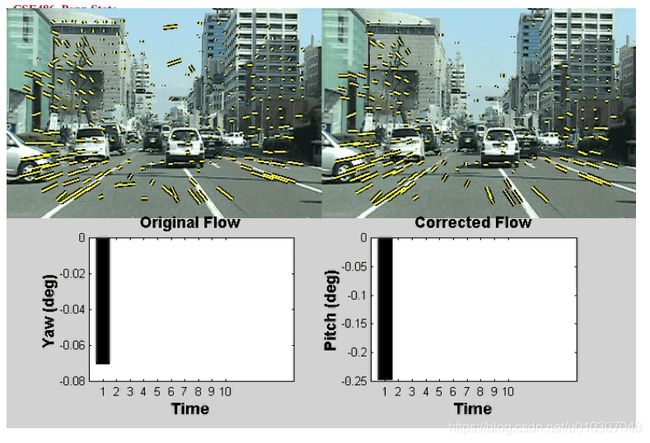
应用：将车辆流场分解为旋转和平移分量
动机
• 估计转向角
• 当移除旋转运动时，简化了场景结构的计算
回顾：由于自身运动产生的场
流（Flow）：
方法
利用汽车可能的运动的先验知识来简化问题。
假设我们知道平移（Tx，Ty，Tz）的近似方向
[例如，如果向前行驶，我们选择（0,0,1）]
假设滚转角（wz）为0
问题简化为解决俯仰角和偏航角（wx和wy）
对于每个观测到的流矢量，通过取流方程和一个新矢量（该矢量被构造成“消除”平移分量）的点积，在wx和wy上形成一个线
性约束。
这个消除矢量为
这其中所有的量都是已知的。
验证：
对于每个观测到的流矢量，我们消除平移分量以形成形式为（ai wx+bi wy+ci）=0 的一个线性约束。
给定n个观测流矢量的集合，我们寻找同时满足n个线性方程组的wx和wy
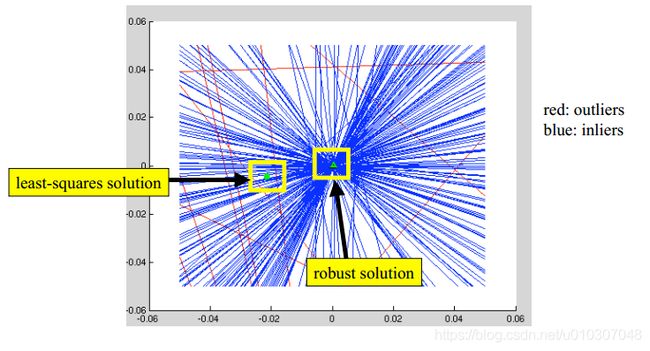
使用鲁棒估计器
使用最小二乘法求解将对外点（严重错误的数据）敏感。
相反，我们使用鲁棒估计（随机样本一致性-RANSAC）。
