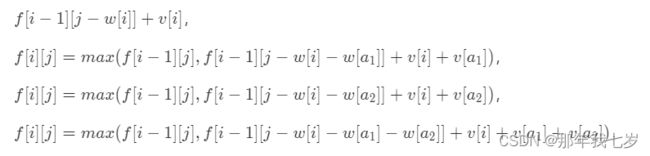01 背包算法
描述
王强决定把年终奖用于购物,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
| 主件 | 附件 |
| 电脑 | 打印机,扫描仪 |
| 书柜 | 图书 |
| 书桌 | 台灯,文具 |
| 工作椅 | 无 |
如果要买归类为附件的物品,必须先买该附件所属的主件,且每件物品只能购买一次。
每个主件可以有 0 个、 1 个或 2 个附件。附件不再有从属于自己的附件。
王强查到了每件物品的价格(都是 10 元的整数倍),而他只有 N 元的预算。除此之外,他给每件物品规定了一个重要度,用整数 1 ~ 5 表示。他希望在花费不超过 N 元的前提下,使自己的满意度达到最大。
满意度是指所购买的每件物品的价格与重要度的乘积的总和,假设设第�i件物品的价格为�[�]v[i],重要度为�[�]w[i],共选中了�k件物品,编号依次为�1,�2,...,��j1,j2,...,jk,则满意度为:�[�1]∗�[�1]+�[�2]∗�[�2]+…+�[��]∗�[��]v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk]。(其中 * 为乘号)
请你帮助王强计算可获得的最大的满意度。
输入描述:
输入的第 1 行,为两个正整数N,m,用一个空格隔开:
(其中 N ( N<32000 )表示总钱数, m (m <60 )为可购买的物品的个数。)
从第 2 行到第 m+1 行,第 j 行给出了编号为 j-1 的物品的基本数据,每行有 3 个非负整数 v p q
(其中 v 表示该物品的价格( v<10000 ), p 表示该物品的重要度( 1 ~ 5 ), q 表示该物品是主件还是附件。如果 q=0 ,表示该物品为主件,如果 q>0 ,表示该物品为附件, q 是所属主件的编号)
输出描述:
输出一个正整数,为张强可以获得的最大的满意度。
示例1
输入:
1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0
复制输出:
2200
复制
示例2
输入:
50 5 20 3 5 20 3 5 10 3 0 10 2 0 10 1 0
复制输出:
130
复制说明:
由第1行可知总钱数N为50以及希望购买的物品个数m为5; 第2和第3行的q为5,说明它们都是编号为5的物品的附件; 第4~6行的q都为0,说明它们都是主件,它们的编号依次为3~5; 所以物品的价格与重要度乘积的总和的最大值为10*1+20*3+20*3=130
算法实现思路:
这个是背包算法的变种;普遍背包算法是:result = max(选择当前物品,不选择当前物品);
不选择当前物品表示最优解是上一行计算的最有解,选择当前物品表示:先计算当前物品,剩下的空间再计算最优解他们的和便是选择当前物品的最优解;
例如: 物品1:价格 3 满意度 3 ;物品2: 价格2 满意1 只有9块钱,物品不可以重复,怎么达到最佳满意度;result[i][j] = max(result[i-1][j], data[i].v+result[j-data[i].p]);data[i].v表示当前物品满意度,data[i].p表示物品的价格,j表示手里的钱,除去选择当前物品的钱,剩下的钱我能买到最满意的是result[j-data[i].p];
先计算只有物品1的情况下,第一行满意度数据result[]; 第二行就需要两件物品,单我不选择物品2时,那么就只有物品1,也就意味着当选择当前物品,满意度就是上一个满意度的数据也就是result[i-1][j];j表示的是价格,i表示的是当前物品;所以当前满意度为:result[i][j] = max(result[i-1][j], data[i].v+result[j-data[i].p]);data[i].v
| 价格1 | 价格2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 物品0~1 | 0 | 0 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 物品0~2 | 0 | 0 | 3 | 3 | 4 | 4 | 4 | 4 | 4 |
| 物品0~3 | |||||||||
| 物品0~4 |
普通背包算法如上,但是当前题是背包算法的一种变种,一个物品分为主件,副主件,一个主件有可能有两个副件,那么就有四种可能:
第一种:只选主件
第二种:主件+附件1
第三种:主件+附件2
第四种:主件+附件1+附件2
主件和副件看成一个整体,所以后面需要加上附件满意度;代码如下:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int totle = in.nextInt()/10;//总钱数
int num = in.nextInt(); // 可购买数量
Entry[] data = new Entry[num];
for (int i = 0; i < num; i++) {
int p = in.nextInt()/10;
int w = in.nextInt() * p;
int parent = in.nextInt();
data[i] = new Entry(p, w, parent);
}
// 绑定主件下的副件
for (int i = 0; i < num; i++) {
int parent = data[i].parent;
if (parent > 0) {
if (data[parent - 1].child1 == -1) {
data[parent - 1].child1 = i;
} else {
data[parent - 1].child2 = i;
}
}
}
int[] result = new int[totle+1];
for (int i = 0; i < num; i++) {// 物品
int[] r = new int[totle+1];
for (int j = 0; j <=totle; j++) {// 价格
r[j] = result[j];
if (data[i].parent > 0) {
continue;
}
// 只有主件
if (j>=data[i].price){
r[j] = Math.max(result[j], data[i].weight+result[j-data[i].price]);
}
// 主件+附件1
if (data[i].child1>0 && j>=(data[i].price+data[data[i].child1].price)){
r[j] = Math.max(r[j],result[j-data[i].price-data[data[i].child1].price]+data[data[i].child1].weight +data[i].weight);
}
// 主件+附件2
if (data[i].child2>0 && j>=(data[i].price+data[data[i].child2].price)){
r[j] = Math.max(r[j],
data[i].weight + data[data[i].child2].weight+ result[j-data[i].price-data[data[i].child2].price]);
}
// 主件+附件1+附件2
if (data[i].child2>0 && j>= (data[i].price+data[data[i].child1].price +data[data[i].child2].price)){
r[j] = Math.max(r[j], data[i].weight+result[j-data[i].price - (data[data[i].child1].price) - (data[data[i].child2].price)]+data[data[i].child1].weight+data[data[i].child2].weight);
}
}
result = r;
// System.out.println(Arrays.toString(result));
}
System.out.println(result[totle]*10);
}
public static class Entry {
public int price;
public int weight;
public int parent = 0;
public int child1 = -1;
public int child2 = -1;
public Entry(int price, int weight, int parent) {
this.price = price;
this.parent = parent;
this.weight = weight;
}
}
}遇坑:
1.后面有附件情况下需要和前面只有主件情况下的结果进行比较,避免只有主键情况下最优,
2.r[j] = result[j]; 先赋值给中间缓存,避免四种情况都不满足的时候使用上一个物品的结果;当前价格小于当前物品,有可能上一个物品满足要求
if (j>=data[i].price){
r[j] = Math.max(result[j], data[i].weight+result[j-data[i].price]);
}