玩转红黑树:手把手教你实现和理解红黑树
玩转红黑树:手把手教你实现和理解红黑树
- 引言
- 一、红黑树的定义
-
- 1.1、理论知识
- 1.2、代码实现
- 1.3、代码优化
- 二、红黑树的旋转
-
- 2.1、理论知识
- 2.2、代码实现
- 三、红黑树插入节点
-
- 3.1、理论知识
- 3.2、代码实现
- 四、红黑树删除节点
-
- 4.1、理论知识
- 4.2、代码实现
- 五、红黑树的查找
-
- 5.1、理论知识
- 5.2、代码实现
- 六、完整代码
- 总结
引言
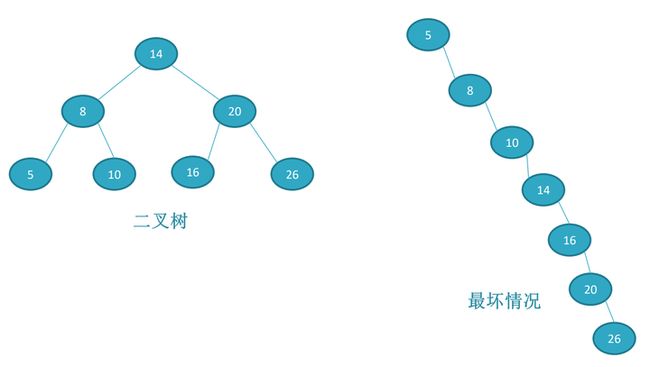
相信学习过编程的都或多或多或少的听说过“红黑树”,在了解红黑树之前,需要明白它是一个二叉树,那么在哪些场景/地方使用过红黑树呢?
- java的hash map。
- Linux系统的CFS公平调度算法。
- 多路复用器 epoll。
- 定时器。
- nginx 等。
上面这些都是使用红黑树的经典场景。红黑树是一个非常常用的数据结构,它有两种用法:
(1)当作Key-Value对,用于查找;通过Key去查找Value。Key是红黑树中构建出来的一个二叉树;比如,当向二叉树里插入一个节点时,红黑树通过比较Key来确定插入的位置。
(2)红黑树是一个二叉排序树,它的中序遍历是顺序的,可以用来作为顺序执行,适合范围查询。

典型的Key-Value数据结构,举个例子:github上的一个流量统计功能(Traffic)。

这两个表中,可以把Site(从哪个网站跳转过来的)作为Key,Views(访问的次数)作为Value;同样的,可以将Content(项目中的哪个资源)作为Key,Views(访问的次数)作为Value。这就是典型的Key-Value结构,针对这样的一个结构可以构建出一个红黑树进行存储。当再次访问相同的资源的时候,可以通过查询红黑树中对应的节点,然后对访问次数(Value)进行加一,从而达到统计的效果。
红黑树的典型使用方式,以epoll为例,当将海量的IO加到epoll中管理时,那么一个数据到达时epoll如何知道是哪个IO的呢?这就涉及到epoll内部的红黑树key-value查找过程;epoll通过红黑树查找到对应的key,从而获取到相应的value。
Key-Value是一种强查找的过程,数据结构主要有以下几种:
- 红黑树。
- hash table。
- B / B+ 树。
- 跳表。
当然,用其他的数据结构也可以实现强查找过程,比如链表,但是它的性能比较低,因为链表的每一次查询都需要从头开始遍历,时间复杂度高。
一、红黑树的定义
1.1、理论知识
红黑树在二叉树的基础上具备如下的性质:
- 每个结点是红的或者黑的。
- 根结点是黑的。
- 每个叶子结点是黑的。
- 如果一个结点是红的,则它的两个儿子都是黑的。
- 对每个结点,从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点 。
满足以上性质的二叉树就是红黑树。其中第五条性质就决定了红黑树的平衡,它不像AVL树那样严格要求两边子树的高度差是1,而是要求黑色节点的高度一致即可。
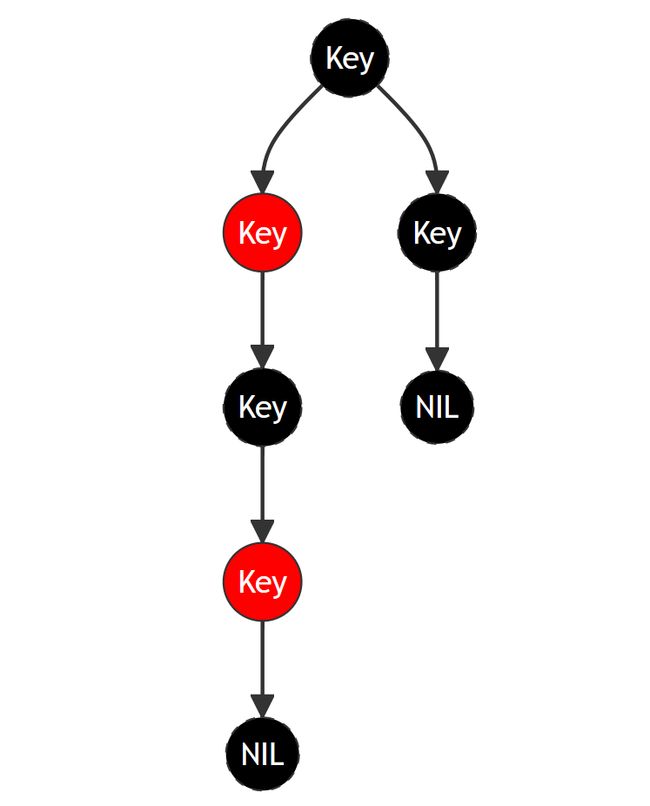
从第四条和第五条的性质中,我们可以总结出一个数学结论:红黑树的根节点到叶子节点的最短路径与红黑树的根节点到叶子节点的最长路径之比是 $ 1 :(2\times N-1)$。
为了检查是否真正理解了红黑树的性质,这里提供如下的判断题,请判断哪个是红黑树,哪个不是:
- 从黑色节点的高度判断,14(黑)–> 8(红)–> NIL(黑),黑高为2;14(黑)–> 8(红)–> 10(黑)NIL(黑),黑高是3。显然不符合红黑树性质中 对每个结点从该结点到其子孙结点的所有路径上的包含相同数目的黑结点 的性质。所有这个不是红黑树。
- 根节点是黑色,黑高都是3,没有连续的红色节点。这个满足红黑树的所有性质,是红黑树。
- 从黑色节点的高度判断,14(黑)–> 8(红)–> NIL(黑),黑高为2;14(黑)–> 8(红)–> 10(黑)NIL(黑),黑高是3。显然不符合红黑树性质中 对每个结点从该结点到其子孙结点的所有路径上的包含相同数目的黑结点 的性质。所有这个不是红黑树。
- 根节点是红色的,所有它也不是红黑树。
1.2、代码实现
了解了理论,就需要代码上进行实现。定义红黑树节点结构体包含以下内容:
- 定义一个颜色标识符。
- 定义左子树和右子树的指针。
- 定义执行父节点的指针。这个是为了做性质调整需要。
- 定义Key和Value。
typedef struct _rbtree_node {
int key;
void* value;
struct _rbtree_node *left;
struct _rbtree_node *right;
struct _rbtree_node *parent;
unsigned char color;
}rbtree_node;
将颜色定义的变量放在结构体的最后一个可以起到节省内存的目的。
定义红黑树的头节点结构体包含以下内容:
- 指向红黑树开始位置的根节点root。
- 根据红黑树的性质,所有的叶子节点都是黑色的,可以把所有的叶子节点都指向同一个点,并且隐藏(也就是NIL节点)。
- 如果需要,还可以定义指向value最小、最大的节点从而提高效率。
typedef struct _rbtree {
struct _rbtree_node *root;
struct _rbtree_node *nil
// 如果需要
//struct _rbtree_node *min;//指向value最小的节点
//struct _rbtree_node *max;//指向value最大的节点
}rbtree;
使用自定义的NIL节点而不是使用NULL的原因是这个NIL节点必须具备红黑树的所有性质。它是为了红黑树的各种操作易于判断,如果使用NULL,我们就无法操作它。
这样,红黑树的定义就完成了。当阅读一份项目源码时,如果看到一个结构体包含颜色定义、左节点、右节点、父节点时,可以大概率确定它是红黑树了。
1.3、代码优化
上面的红黑树定义是否存在一些问题呢?最大的问题是这个红黑树的定义不可复用,它的业务和红黑树的实现是黏在一起的,可迁移性低。
为了提高通用性和灵活性,可以将红黑树的定义做成模板化,将红黑的性质封装在一起。
#define RBTREE_ENTRY(name,type) \
struct name { \
struct type*left; \
struct type*right; \
struct type*parent; \
unsigned char color; \
}
typedef int KEY_TYPE;
typedef struct _rbtree_node {
// 业务相关
KEY_TYPE key;
void* value;
// 红黑树相关
RBTREE_ENTRY(,_rbtree_node);
}rbtree_node ;
typedef struct _rbtree {
struct _rbtree_node *root;
struct _rbtree_node *nil
// 如果需要
//struct _rbtree_node *min;//指向value最小的节点
//struct _rbtree_node *max;//指向value最大的节点
}rbtree;
举个例子,线程有ready(就绪)、wait(等待)、sleep(休眠)、exit(退出)等状态;假设有N个线程,它们状态各不相同,每个状态可以使用红黑树进行存储,那么就可以定义成这样:
#define RBTREE_ENTRY(name,type) \
struct name { \
struct type*left; \
struct type*right; \
struct type*parent; \
unsigned char color; \
}
typedef int KEY_TYPE;
typedef struct _thread_node {
// 业务相关
KEY_TYPE key;
void* value;
// 红黑树相关
RBTREE_ENTRY(,_thread_node) ready;
RBTREE_ENTRY(,_thread_node) wait;
RBTREE_ENTRY(,_thread_node) sleep;
RBTREE_ENTRY(,_thread_node) exit;
}thread_node ;
typedef struct _thread {
struct _thread_node *root;
struct _thread_node *nil
}_thread;
也就是一个结构体可以包含多颗红黑树。
二、红黑树的旋转
当红黑树的性质被破环时,需要触发旋转,进行调整。旋转是为了不影响其他的性质,然后更好的变色。
2.1、理论知识
旋转有两种方式:左旋和右旋。这两种旋转是一种互逆的过程。
旋转的目的:保持红黑树的平衡。

左旋(Left Rotation):左旋操作是将一个节点的右子节点变为其父节点,同时将右子节点的左子节点变为该节点的右子节点。
- 让当前节点的右子节点成为新的根节点。
- 将新根节点的左子节点(如果存在)移动为原来节点的右子节点。将原来节点成为新根节点的左子节点。
- 这样,左旋操作完成后,原来节点的右子节点会上升为新的根节点,而原来节点会变为新根节点的左子节点。
右旋(Right Rotation):右旋操作是将一个节点的左子节点变为其父节点,同时将左子节点的右子节点变为该节点的左子节点。
- 让当前节点的左子节点成为新的根节点。
- 将新根节点的右子节点(如果存在)移动为原来节点的左子节点。将原来节点成为新根节点的右子节点。
- 右旋操作会导致原来节点的左子节点上升为新的根节点,而原来节点会变为新根节点的右子节点。
左旋和右旋的过程,改变了哪些东西呢?左旋需要改变三个方向共六个指针的指向,以上图为例:
- 改变X的右指针。
- 改变Y的左指针。
- 改变X父结点的指针。
这三个指针是双向的,所以是六个指针(比如X的右指针指向Y,Y的父指针指向X)。即X的右指针改为指向Y的左结点,Y的左指针改为指向X,X的父结点指针改为指向Y。
右旋与左旋同理,它们是一个互逆的过程。
以根结点示例:
小结:红黑树插入或删除节点,最多需要旋转的次数是树的高度。
2.2、代码实现
(1)左旋。左旋函数的实现需要带哪些形参呢?答案是头节点和旋转节点。
- 从红黑树的定义上可以知道,传入头节点的目的是我们需要判断左子树和右子树是不是叶子节点以及判断旋转节点的父节点是不是根节点,因为头节点存储着叶子节点nil和根节点root。
- 需要改变的指针指向:改变x的右指针指向和y左子树的父指针指向;改变y的父指针指向和x的父节点左子树的指向;改变y的左指针指向和x的父指针指向。
/**********************红黑树左旋 start***************************/
void rbtree_left_rotate(rbtree *T,rbtree_node *x)
{
rbtree_node *y = x->right;
// 1. 改变x的右指针指向和y左子树的父指针指向,这里需要判断y的左子树是否是叶子节点
x->right = y->left;
if (y->left != T->nil)
{
y->left->parent = x;
}
// 2. 改变y的父指针指向和x的父节点左子树的指向,这里需要判断x是不是根节点以及判断x节点是其父节点的左子树还是右子树
y->parent = x->parent;
if (x->parent == T->nil) // 根节点
T->root = y;
else if (x == x->parent->left) // 左子树
x->parent->left = y;
else
x->parent->right = y;
// 3. 改变y的左指针指向和x的父指针指向
y->left = x;
x->parent = y;
}
/**********************红黑树左旋 end***************************/
(2)右旋。左旋和右旋是互逆的,右旋过程和左旋过程同理,学会了左旋,右旋就更简单了。
/**********************红黑树右旋 start***************************/
/*
* x改为y,y改为x,右改为左,左改为右
*
*****************************************************************/
void rbtree_right_rotate(rbtree *T, rbtree_node *y)
{
rbtree_node *x = y->left;
// 1
y->left = x->right;
if (x->right != T->nil)
{
x->right->parent = y;
}
// 2
x->parent = y->parent;
if (y->parent == T->nil)
T->root = x;
else if (y == y->parent->right)
y->parent->right = x;
else
y->parent->left = x;
// 3
x->right = y;
y->parent = x;
}
/**********************红黑树右旋 end***************************/
三、红黑树插入节点
3.1、理论知识
红黑树本质上是一个二叉树,所以它的插入过程和二叉树的插入过程相似。从根节点开始,比当前节点大的走右子树,比当前节点小的走左子树。比如如下的插入12这个节点:
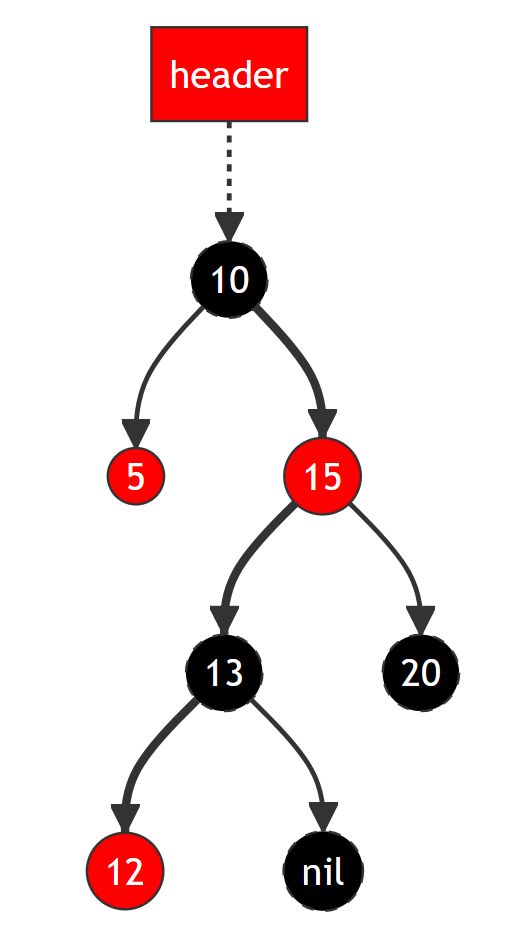
当插入结点时,可以推断出以下情况(比如插入的结点是z):
(1)z肯定是红色;
(2)z的父节点是红色;
(3)z的祖父结点肯定是黑色;
(4)z的叔结点颜色不确定。
所以,判断条件主要在叔父节点上。最简单的示例如下:
更复杂的例子,先以 父结点是祖父结点的左子树的情况(假设插入的节点是z):
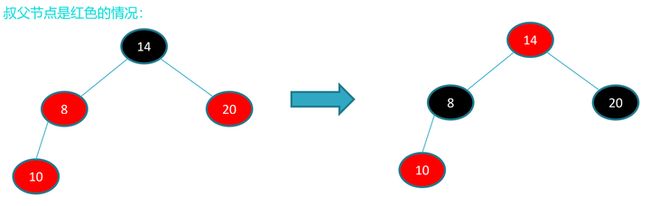
(1)叔节点是红色;这种情况最简单,这个状态下树本身的重量是平衡的,不需要旋转,直接将父节点和叔节点变黑色,祖父节点变红色。
(2)叔结点是黑色的,而且当前结点是右孩子。可以看到祖父节点的左边节点比较多而右边比较少,将当前指针保存的节点变为保存父节点,然后从当前节点执行左旋操作,让当前节点变成左子树。这是一个中间状态,还需要下一步操作才能平衡。
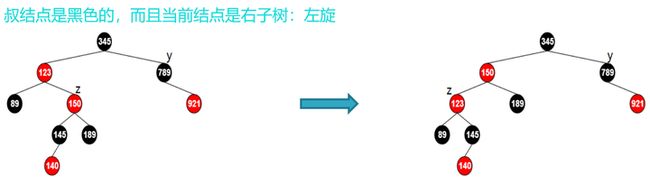
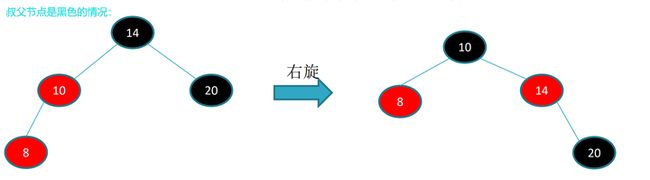
(3)叔结点是黑色的,而且当前结点是左孩子 。可以看到祖父节点的左边节点比较多而右边比较少,所以需要祖父节点执行右旋操作,并进行变色;最终达到平衡。
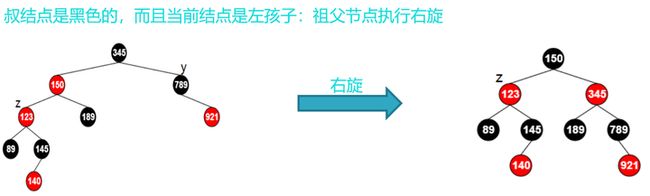
插入节点的过程主要就是这三种状态,理解了父结点是祖父结点的左子树的情况,那么理解父结点是祖父结点的右子树的情况就容易多了。
父结点是祖父结点的右子树的情况与父结点是祖父结点的左子树的情况是相似的,这里就不赘述了。
3.2、代码实现
插入步骤:
- 插入的节点都是先插入到最底层,但在隐藏的叶子节点之前。
- 在查找叶子节点的过程中,如果遇到key相等的情况可以采取两种方案:丢弃和微调key。比如定时器上的红黑树以时间戳为key,当key相同时可以微调key的大小再插入。这意味着相等的情况取决于业务场景,而不是由红黑树本身来决定。
- 插入前,必须判断当前的红黑树是否是空。
- 红黑树插入结点之前,它已经是一颗红黑树。所以给插入的结点上色是红色,因为这样不会改变黑高,同时出现判断条件:不能有连续的红色节点;然后做调整。
/**********************红黑树插入 start***************************/
// 调整
void rbtree_insert_fixup(rbtree *T, rbtree_node *z)
{
// 红黑树特性之一:如果一个结点是红的,则它的两个儿子是黑的
while (z->parent->color == RED)
{
if (z->parent == z->parent->parent->left)
{
rbtree_node *y = z->parent->parent->right;
if (y->color == RED)//叔父结点为红色
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
// 保证 Z 永远是红色,才能调整
z = z->parent->parent;
}
else //y==black
{
if (z == z->parent->right)
{
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
//祖父结点旋转
rbtree_right_rotate(T, z->parent->parent);
}
}
else
{
rbtree_node *y = z->parent->parent->left;
if (y->color == RED)//叔父结点为红色
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
// 保证 Z 永远是红色,才能调整
z = z->parent->parent;
}
else {
if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
// 插入到底部
void rbtree_insert(rbtree *T, rbtree_node *z)
{
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil)
{
y = x;
if (z->key < x->key)
x = x->left;
else if (z->key > x->key)
x = x->right;
else
return;
}
z->parent = y;
if (y == T->nil)
T->root = z;
else {
if (y->key > z->key)
y->left = z;
else
y->right = z;
}
z->left = z->right = T->nil;
z->color = RED;
rbtree_insert_fixup(T, z);
}
/**********************红黑树插入 end***************************/
四、红黑树删除节点
4.1、理论知识
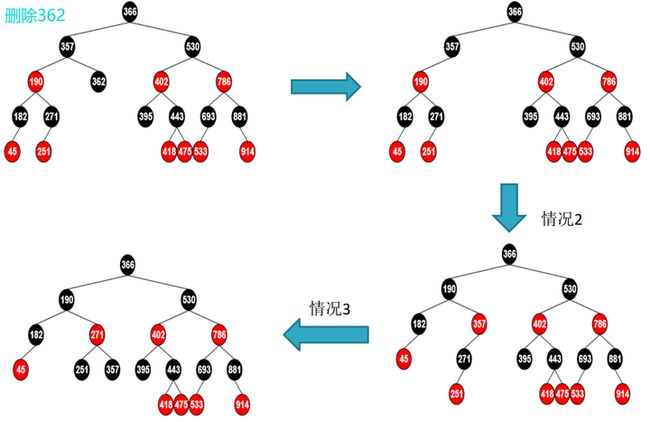
红黑树的删除分如下几种情况:
(1)没有左右子树。直接删除,比如:
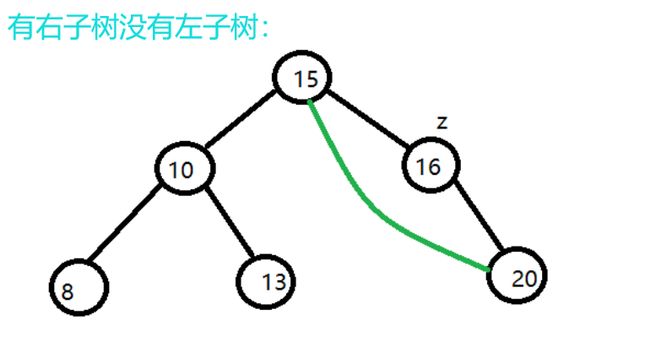
(2)有左子树或者右子树。修改父节点的子树指向当前节点的左子树或者右子树,然后删除当前节点。比如:
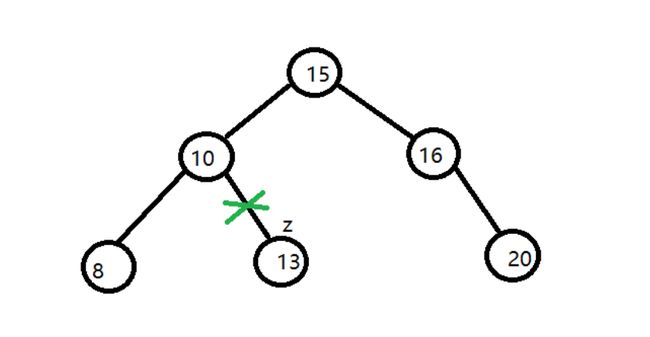
(3)有左子树且有右子树,需要找到覆盖节点、 删除节点、轴心节点。比如下面的示例, 10是覆盖节点、11是删除节点,12是轴心节点:

(4)先讨论当前结点是父结点的左子树的情况。
1)当前结点的兄弟结点是红色的。删除当前节点,改变父节点为红色,同时改变兄弟节点为黑色,再进行右旋调整。
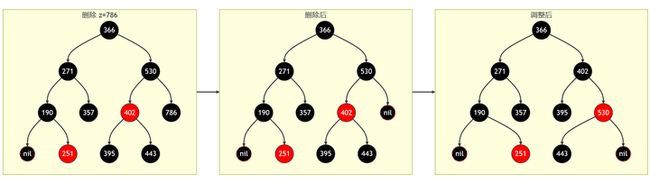
2)当前结点的兄弟结点是黑色的,而且兄弟结点的两个孩子结点都是黑色的。删除当前节点,修改兄弟节点和叔父节点为红色。

3) 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是红色的,右孩子是黑色的当前结点是父结点的左子树的情况。
4) 当前结点的兄弟结点是黑色的,而且兄弟结点的右孩子是红色的。

(5)当前结点是父结点的右子树的情况。这种情况和【当前结点是父结点的左子树的情况】同理。
4.2、代码实现
/**********************红黑树删除 start***************************/
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
while (x->left != T->nil) {
x = x->left;
}
return x;
}
rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
while (x->right != T->nil) {
x = x->right;
}
return x;
}
rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x)
{
rbtree_node *y = x->parent;
if (x->right != T->nil)
{
return rbtree_mini(T, x->right);
}
while ((y != T->nil) && (x == y->right)) {
x = y;
y = y->parent;
}
return y;
}
//调整
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) {
if (x == x->parent->left) {
rbtree_node *w = x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_left_rotate(T, x->parent);
w = x->parent->right;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
}
else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
rbtree_right_rotate(T, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rbtree_left_rotate(T, x->parent);
x = T->root;
}
}
else {
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
}
else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z)
{
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
if ((z->left == T->nil) || (z->right == T->nil))
{
y = z;
}
else
{
y=rbtree_successor(T, z);
}
if (y->left != T->nil)
x = y->left;
else if (y->right != T->nil)
x = y->right;
x->parent = y->parent;
if (y->parent == T->nil)
T->root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
if (y != z)
{
z->key = y->key;
z->value = y->value;
}
// 调整
if (y->color == BLACK) {
rbtree_delete_fixup(T, x);
}
return y;
}
/**********************红黑树删除 end***************************/
五、红黑树的查找
5.1、理论知识
红黑树首先是一颗二叉搜索树,也就是每个节点的左子树中的值都小于它自身的值,而右子树中的值都大于它的值,这样可以通过比较大小来逐步缩小查找范围。
查找操作在红黑树中与普通二叉搜索树类似。从根节点开始,递归地比较要查找的值与当前节点的值。如果要查找的值比当前节点值小,就继续在左子树中查找;如果要查找的值比当前节点值大,就继续在右子树中查找;如果相等,则找到了目标节点。
5.2、代码实现
/**********************红黑树查找 start***************************/
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {
rbtree_node *node = T->root;
while (node != T->nil) {
if (key < node->key) {
node = node->left;
}
else if (key > node->key) {
node = node->right;
}
else {
return node;
}
}
return T->nil;
}
/**********************红黑树查找 end***************************/
六、完整代码
代码已上传github和gitee。github:RedBlackTree
总结
红黑树需要理解的难点:性质、旋转、插入、删除。
- 红黑树是一种二叉树,中序遍历绝对有序。当红黑树的性质被破环时,需要触发旋转,进行调整。
- 旋转有两种方式:左旋和右旋。
- 红黑树具有以下性质:
- 结点不是红色就是黑色;
- 每个叶子结点一定是黑色;
- 根节点一定是黑色;
- 如果一个结点是红的,则它的两个儿子是黑的;
- 对每个节点,从该结点到其子孙结点的所有路径上,都包含相同数目的黑结点;即黑高。这决定红黑树的平衡。
红黑数平衡主要是平衡黑高,即任一结点到其子叶子结点的黑色结点数量相同。红黑树的插入和删除会影响红黑树的性质,需要做调整。
扩展补充,linux下编写代码的环境:
- vmware+Ubuntu。提供虚拟系统。
- samba + ssh。将Linux系统映射到本地。
- gcc/g++编译器。
- vscode/sourceinsight/qtcreater编辑器。