LeetCode刷题笔记2
文章目录
-
- 一、双指针
-
- 80.删除排序数组中的重复项2
- 二、递归
-
- 83. 删除排序链表中的重复元素
- 82. 删除排序链表中的重复元素2
- 94.二叉树的中序遍历
- 98.验证二叉搜索树
- 101. 对称二叉树
- 105.从前序与中序遍历序列构造二叉树
- 114.二叉树展开为链表
- 三、动态规划
-
- 91.解码方法
- 四、回溯
-
- 47.全排列2
一、双指针
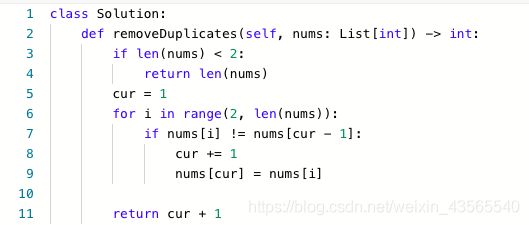
80.删除排序数组中的重复项2
本题重点在理解。首先原地删除肯定是用双指针,其次要理解每个指针的实际含义。cur指针相对固定,可以理解为展示当前数组的“布”,cur后面都是我们看不到的地方,i指针用于遍历,判断后面的地方有没有数能够加入当前数组,如果能加入,就把cur指针向后移动一位,并且把i指向的内容复制到cur上。
二、递归
有关递归的问题我认为这篇文章讲的很好:递归详解
在进行递归时,核心是搞清楚三个部分的内容:一是递归终止的条件,二是递归中每一环节需要做什么,三是每一步骤需要返回什么。
下面以两道题为例:
83. 删除排序链表中的重复元素
尝试用递归来完成:
- 第一步:递归结束的条件。若当前节点为空或者当前节点的下一个节点为空时,显然不再需要进行排序,因此递归结束。
写成代码:
if node == none or node.next == none:
return node
- 第二步:确定每一步需要做什么。宏观上考虑,我们只需要判断当前节点与后面的一个节点是否是重复值,并且此时node.next已经指向一个已经剔除重复值的链表了,所以我们只需要判断node与node.next是否相等。
- 第三步:考虑要返回什么值,作为一个链表自然是要返回表头了。
把第二步和第三步写成代码:
node.next = fuc(node.next)
if node.value == node.next.value:
node = node.next
return node
写成最终代码:
class Solution:
def deleteDuplicates(self, head: ListNode) -> ListNode:
if head == None or head.next == None:
return head
head.next = self.deleteDuplicates(head.next)
if head.val == head.next.val:
head = head.next
return head
82. 删除排序链表中的重复元素2
这一题有点困难,我们先按照83的思路给出一个错误的分析方法:
- 第一步,确定结束条件,这个没问题
- 第二步,确定每一步要干什么,我们这里是如果遇到重复值就把所有的重复值就删掉,那么当
head.val == head.next.val发生时,应该把head指向head.next.next,看起来似乎并没有问题。
写出最终代码:
def deleteDuplicates(head):
if head == None or head.next == None:
return head
head.next = deleteDuplicates(head.next)
if head.val == head.next.val:
head = head.next.next
return head
对测试用例[1,2,3,3,4,4,5]运行,结果是对的,但对测试用例[1,1,1,3,4]运行,结果就是[1,3,4]了,发生了错误,这里错误的原因在于该代码只能处理重复两次的情形,比如程序从后向前,当发现[1,1,3,4]中存在重复数字时,会返回[3,4]这就导致前面的1会认为后面不存在重复数字。
把算法进行如下修改,不再是从后向前,而是从前向后:
- 设置两个指针p,q,p指向head,q指向head.next,如果p.value == q.value,则表示已经发生重复,将q不断向后移动直到p.value != q.value为止,然后把p直接指向此时的q.如果p.value != q.value,表示没有发生重复,p不变,进行下一层递归。
def deleteDuplicates(head):
if head == None or head.next == None:
return head
nextnode = head.next
if head.val == nextnode.val:
while(nextnode != None and head.val == nextnode.val):
nextnode = nextnode.next
head = deleteDuplicates(nextnode)
else:
head.next = deleteDuplicates(nextnode)
return head
94.二叉树的中序遍历

二叉树结构天生适合递归,因为它在每一层要做的事情都是类似的。
比如我们在某一步骤上,能看到的二叉树是这样的:
那么首先我们要先进入左子树,并且假定此时用于递归的函数已经完成了左子树的遍历,并返回了正确的结果,所以接下来第二步是将根节点的值加入到遍历列表中,第三步则是进入右子树的遍历。
至于递归结束的条件,很显然是当树为空时递归结束,返回到上一层。
def backtrack(root, path):
if not root:
return
backtrack(root.left, path)
path.append(root.val)
backtrack(root.right, path)
写成完整的程序:
def inorderTravel(root):
path = []
backtrack(root, path)
return path
以上是递归的思想解决问题,下面用迭代的方法:
用迭代的方法就要顺着二叉树按顺序往下,
第一步,先遍历完左子树,并且把节点压入栈
第二步,左子树遍历完后,开始向上走,弹出栈顶元素,记录值
第三步,如果栈顶元素有右子树,再进行右子树遍历。
def inorderTravel(root):
path = []
stack = []
while(root):
stack.append(root)
root = root.left
while(stack):
root = stack.pop()
path.append(root.val)
root = root.right
while(root):
stack.append(root)
root = root.left
return path
98.验证二叉搜索树
要确定是否是二叉搜索树,就是按照左子树-根节点-右子树的顺序访问二叉树,然后判断每个节点上的值是否是递增的,如果是递增的就是二叉搜索树,否则不是。因此用递归的方法和94题的结论是一样的,只不过要多出一个对path的检查。
不过这种方法在空间和时间上的浪费比较多,我们考虑是否能在迭代的过程中就加入对大小关系的判断。
def isValidBST(root):
stack = []
pre = float('-inf')
while root:
stack.append(root)
root = root.left
while stack:
root = stack.pop()
if root.val < pre:
return False
pre = root.val
root = root.right
while(root):
stack.append(root)
root = root.left
return True
101. 对称二叉树

本题也非常能体现递归的思想,首先在节点处,我们需要比较当前左右子节点(记为left, right)是否相等,同时要接着比较left.left和right.right以及left.right和right.left是否相等,这就涉及到逐层递归了。
def check(left, right):
if not left and not right:
return True
if not left or not right:
return False
if left.val == right.val and check(left.left, right.right) and check(left.right, right.left):
return True
else:
return False
def isSymmeric(root):
if not root:
return True
return check(root.left, root.right)
105.从前序与中序遍历序列构造二叉树
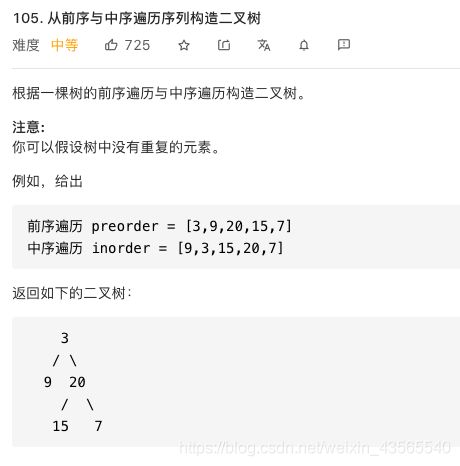
前序遍历是按照“根节点- 左子树 - 右子树”的顺序进行遍历,中序遍历是按照“左子树- 根节点- 右子树”顺序进行遍历,仅根据其中一种方法无法确定完整的树。
首先根据前序遍历的第一个值确定根节点,然后在中序遍历中找到根节点所在的位置,左边的元素构成左子树,右边的元素构成右子树,由此确定左子树的规模,并再次返回前序遍历列表,确定左右子树的根节点。由此可以进行递归。
def buildTree(preorder, inorder):
if not preorder:
return None
root = TreeNode(preorder[0])
mid = inorder.index(preorder[0])
root.left = buildTree(preorder[1:(mid + 1)], inorder[:mid])
root.right = buildTree(preorder[mid+1:], inorder[mid+1:])
return root
114.二叉树展开为链表

本题仍然是利用了中序遍历的方法进行展开,首先从根节点出发,找到左子树,把左子树放到右子树的位置上,然后把右子树放到左子树的最右边的节点后面。
def flatten(root):
while(root):
if root.left:
prev = root.left
while prev.right:
prev = prev.right
prev.right = root.right
root.right = root.left
root.left = None
root = root.right
else:
root = root.right
三、动态规划
动态规划问题,另一个难题。
经验来说,主要难点在于确定状态转移方程和边界条件,有的时候为了降低空间复杂度还需要做优化。
91.解码方法
对本题来说,只需要给出结果,不需要给出每种编码内容,因此不需要使用回溯算法进行搜索,偏向使用动态规划。
首先确定边界条件:
- 当s[0]为0时,肯定编码失败,直接返回0
然后确定状态转移方程:
- 如果
s[i] == '0',只有当s[i-1] == 1 or 2时,可以编码成功,并且一定是和s[i-1]一起编码,否则编码失败,返回0 - 如果
s[i - 1] == '1',则一定会编码成功,并且有两种编码情况,一是s[i]和s[i-1]一起编码,二是单独编码 - 如果
s[i-1] == '2',则还需要考虑s[i]的大小,如果在1~6之间,则编码成功,并且也有两种情况。
注意这里涉及到动态规划的一个重要思想:
分类计数加法
分步计数乘法
像上面的情况,有两种编码情况时,最后的结果是相加,而从dp[i-1]到dp[i]则是乘法,只是这里的解码方法通常只有1种,因此一般是直接赋值。
同时注意到这里只有s[i], s[i-1], s[i-2]发挥作用,因此可以优化存储空间。
def numDecoding(s):
# 边界条件
if s[0] == '0':
return 0
prev, cur = 1, 1
for i in range(1, len(s)):
temp = cur
if s[i] == '0':
if s[i-1] == '1' or s[i-1] == '2':
cur = prev * 1
else:
return 0
elif s[i-1] == '1' or (s[i-1] == '2' and '1' <= s[i] <= '6'):
cur = cur + prev
prev = temp
return cur
四、回溯
47.全排列2
- 画出递归树,找到状态变量。本题中递归树每一层在绘制过程中要注意:①每个子节点都需要选择父节点选择后的数字;②由于数字排列中可能存在重复数字,因此结果中也会出现重复排列,需要考虑剪枝,剪枝需要对每个子节点的生成施加一些条件。这里我们就需要添加状态变量
used = [False for _ in range(len(nums))]用于记录每个数字是否被使用 - 结束条件:当树到达底层的时候结束
- 确定选择列表。总的选择列表应该是所有数组中上一层没有选择的数字。
- 判断是否需要剪枝。这里需要剪枝,剪枝的条件应该是:当前数字与上一个数字重复,并且上一个数字还没有使用过。
- 做出选择,进入下一层
- 撤销选择
def permuteUnique(nums):
nums.sort()
results = []
used = [False for _ in range(len(nums))]
def backtrack(nums, path):
if len(nums) == len(path):
results.append(list(path))
return
for i in range(len(nums)):
if not used[i]:
if i > 0 and nums[i] == nums[i-1] and not used[i-1]:
continue
path.append(nums[i])
used[i] = True
backtrack(nums, path)
used[i] = False
path.pop()
backtrack(nums, [])
return results