力扣做题笔记

力扣做题笔记

---

---

一、Easy

240. 搜索二维矩阵2

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。 每列的元素从上到下升序排列。

朴素的想法是二分查找
但是最好的方式是Z字型查找，从矩阵的右上角开始遍历，向左是变小，向下是变大。

def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
    x = 0
    y = len(matrix[0]) - 1
    n = y
    m = len(matrix) - 1
    while x<=m and y >=0:
        if matrix[x][y] == target:
            return True
        elif matrix[x][y] < target:
            x = x+1
            continue
        else:
            y = y-1
            continue
    return False

15. 三数之和

O(n*n)的时间复杂度
首先排序，先固定第一个数，然后在第一个数后面的区间内，双指针向内并拢。
target = -a
如果b+c > target,right–,
如果b+c b+c == target, 就存入ans中
left==right的时候跳出

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        nums.sort()
        ans = list()
        
        # 枚举 a
        for first in range(n):
            # 需要和上一次枚举的数不相同
            if first > 0 and nums[first] == nums[first - 1]:
                continue
            # c 对应的指针初始指向数组的最右端
            third = n - 1
            target = -nums[first]
            # 枚举 b
            for second in range(first + 1, n):
                # 需要和上一次枚举的数不相同
                if second > first + 1 and nums[second] == nums[second - 1]:
                    continue
                # 需要保证 b 的指针在 c 的指针的左侧
                while second < third and nums[second] + nums[third] > target:
                    third -= 1
                # 如果指针重合，随着 b 后续的增加
                # 就不会有满足 a+b+c=0 并且 b
                if second == third:
                    break
                if nums[second] + nums[third] == target:
                    ans.append([nums[first], nums[second], nums[third]])
        
        return ans

215. 数组中的第K个最大元素（百度二面）

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

1. 冒泡排序方式

    def findKthLargest(self, nums: List[int], k: int) -> int:
        n = len(nums)
        for j in range(k):
            for i in range(n-2, -1 + j, -1):
                if nums[i+1]>nums[i]:
                    nums[i+1], nums[i] = nums[i], nums[i+1]
        return nums[k-1]

2. 快排方式

def quickSort(left, right, k):
    if left >= right:
        return
    flag = nums[left]
    l = left
    r = right
    while l < r:
        while l < r and nums[r] < flag:
            r -= 1
        while l < r and nums[l] >= flag:
            l += 1
        nums[l], nums[r] = nums[r], nums[l]

    nums[l], nums[left] = nums[left], nums[l]
    if l == k:
        return
    elif l < k:
        quickSort(l+1, right, k)
    else:
        quickSort(left, l-1, k)
        
n = len(nums)
quickSort(0, n-1, k-1)
print(nums)
return (min(nums[:k]))

3. 最大堆方式

堆建立的过程中，将倒数第二层的节点开始进行下沉操作，也就是如果两个子节点有比该节点大的，选取最大的交换
移除堆顶元素的过程就是，把堆顶元素放到最后，然后开始自上而下的下沉
添加元素的时候，先放到末尾，然后不断进行上移操作

"""
最大堆
"""
```python
class MaxHeap(object):
    # def __init__(self):
    #   self.data = []  # 创建堆
    #   self.count = len(self.data)  # 元素数量

    def __init__(self, arr):
        self.data = copy.copy(arr)
        self.count = len(self.data)
        i = self.count / 2
        while i >= 1:
            self.shiftDown(i)
            i -= 1

    def size(self):
        return self.count

    def isEmpty(self):
        return self.count == 0

    def insert(self, item):
        # 插入元素入堆
        self.data.append(item)
        self.count += 1
        self.shiftup(self.count)

    def shiftup(self, count):
        # 将插入的元素放到合适位置，保持最大堆
        while count > 1 and self.data[(count/2)-1] < self.data[count-1]:
            self.data[(count/2)-1], self.data[count-1] = self.data[count-1], self.data[(count/2)-1]
            count /= 2

    def extractMax(self):
        # 出堆
        if self.count > 0:
            ret = self.data[0]
            self.data[0], self.data[self.count-1] = self.data[self.count-1], self.data[0]
            self.data.pop()
            self.count -= 1
            self.shiftDown(1)
            return ret

    def shiftDown(self, count):
        # 将堆的索引位置元素向下移动到合适位置，保持最大堆
        while 2 * count <= self.count :
            # 证明有孩子
            j = 2 * count
            if j + 1 <= self.count:
                # 证明有右孩子
                if self.data[j] > self.data[j-1]:
                    j += 1
            if self.data[count-1] >= self.data[j-1]:
                # 堆的索引位置已经大于两个孩子节点，不需要交换了
                break
            self.data[count-1], self.data[j-1] = self.data[j-1], self.data[count-1]
            count = j

139. 单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

一维数组动态规划：以当前点为结尾是否是可以被拼成单词的

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        n = len(s)
        dp = [False for _ in range(n+1)]
        dp[0] = True
        for i in range(n):
            for j in range(i+1, n+1):
                if dp[i] == True and s[i:j] in wordDict:
                    dp[j] = True
        return dp[n]

206. 反转链表(easy)

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

用的是迭代的方式，一开始初始一个空点作为第一个点的后继，然后不断将这个点赋值为当前的点，这样下一个点就可以指向当前点。
指到的最后一个点就是我们需要的新头结点。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        if not head:
            return None
        nx = None
        cur = head
        chil = cur.next
        while chil:
            chil = cur.next
            cur.next = nx
            nx = cur
            if chil:
                cur = chil
            else:
                break
        return cur

11. 盛最多水的容器（medium）

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

双指针+贪心

class Solution:
    def maxArea(self, height: List[int]) -> int:
        n = len(height)
        l = 0
        r = n-1
        ans = 0
        while l < r:
            nowhigh = min(height[l], height[r])
            ans = max(ans, nowhigh*(r-l))
            if height[l] < height[r]:
                l += 1
            else:
                r -= 1
        return ans

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

双指针做法：
定义log为头结点的父节点，l一开始在log，r一开始在head，所以r只需要先走n-1步

        # 只有一个节点特殊判断：
        if n == 1 and head.next == None:
            return None
        log = ListNode(next = head)
        l = log
        r = head
        for _ in range(n-1):
            r = r.next
        lp = l
        while r:
            lp = l
            l = l.next
            r = r.next
        lp.next = l.next

        return log.next

20. 有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。

栈模拟，不放代码了

21. 合并两个有序链表

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        prehead = ListNode(-1)

        prev = prehead
        while l1 and l2:
            if l1.val <= l2.val:
                prev.next = l1
                l1 = l1.next
            else:
                prev.next = l2
                l2 = l2.next            
            prev = prev.next
        # 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 if l1 is not None else l2
        return prehead.next

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

基于(a)b的想法实现，实现的方式比较巧妙，然后需要考虑到format代码的使用

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        # newline = (a)b
        if n == 0:
            return ['']
        ans = []
        for c in range(n):
            for left in self.generateParenthesis(c):
                for right in self.generateParenthesis(n-c-1):
                    ans.append('({}){}'.format(left, right))
        return ans 

53. 最大子数组和

简单的动归

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        dp = []
        for i in range(n):
            if i == 0:
                dp.append(nums[0])
            else:
                dp.append(max(nums[i], nums[i] + dp[i-1]))
        return(max(dp))

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

当前层种类只和前两层有关，加在一起就可以，然后一直迭代

    def climbStairs(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        a, b = 1, 1
        for i in range(2, n+1):
            c = a + b
            a = b
            b = c
        return c

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

可以计数做，更好的方式是亦或

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        nums.sort()
        ans = 0
        for n in nums:
            ans ^= n
        return ans

94. 二叉树的中序遍历

递归很好实现，打算用迭代实现
迭代在思想上其实有不小的难度
实现的时候对于root，一直向左找到尽头的左节点，然后接下来root=root.right，为空的时候就不会重复寻找左节点了

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        ans = []
        if root == None:
            return []
        stack = []
        while root or stack:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            ans.append(root.val)
            root = root.right
        return ans

二、Medium

31. 下一个排列

没有做，优先度不高

33. 搜索旋转排序数组(面试搜狐的时候考过)

整数数组 nums 按升序排列，数组中的值 互不相同 。
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return -1
        l, r = 0, len(nums) - 1
        while l <= r:
            mid = (l + r) // 2
            if nums[mid] == target:
                return mid
            if nums[0] <= nums[mid]:
                if nums[0] <= target < nums[mid]:
                    r = mid - 1
                else:
                    l = mid + 1
            else:
                if nums[mid] < target <= nums[len(nums) - 1]:
                    l = mid + 1
                else:
                    r = mid - 1
        return -1

34. 在排序数组中查找元素的第一个和最后一个位置

就是一个二分查找，然后对位置前后搜索一下。

39. 组合总和 *

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的不同组合数少于 150 个。

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

纯纯的回溯，没意思

46. 全排列 *

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

可以仔细看一下下面的代码，不使用额外空间的回溯，基于前i位向后n-i+1位索取换位的搜索方式

class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        def backtrack(first = 0):
            # 所有数都填完了
            if first == n:  
                res.append(nums[:])
            for i in range(first, n):
                # 动态维护数组
                nums[first], nums[i] = nums[i], nums[first]
                # 继续递归填下一个数
                backtrack(first + 1)
                # 撤销操作
                nums[first], nums[i] = nums[i], nums[first]
        
        n = len(nums)
        res = []
        backtrack()
        return res

48. 旋转图像 *

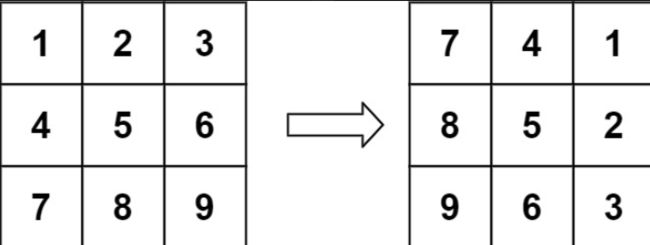
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

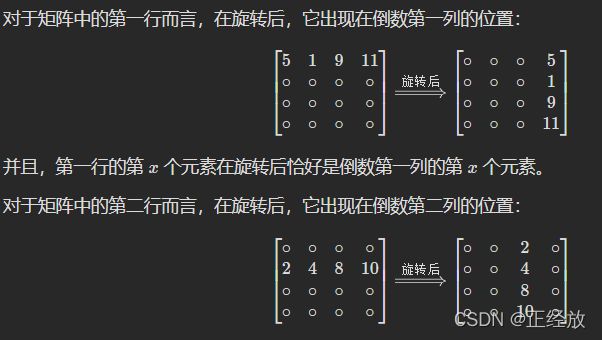
第一种解法就可以新开辟一个二维数组，把老数组的行转到新数组的导数第几列中，但是这样不是个好的办法。

第二种方式是原地旋转：

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)
        for i in range(n//2):
            for j in range((n+1)//2):
                matrix[i][j], matrix[j][n-1-i], matrix[n-1-i][n-1-j], matrix[n-1-j][i] = matrix[n-1-j][i], matrix[i][j], matrix[j][n-1-i], matrix[n-1-i][n-1-j]
        return matrix

49. 字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词，所有源单词中的字母通常恰好只用一次。
输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,“tan”],[“ate”,“eat”,“tea”]]

前两种思路：一个是对所有的字符串排序，一个是对每个字符串进行Counter然后比较是否相同。
对于比较Counter的算法，实现起来还是比较有难度的，有很多小trick

    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        mp = collections.defaultdict(list)
        for st in strs:
            counts = [0] * 26
            for ch in st:
                counts[ord(ch) - ord("a")] += 1
            # 需要将 list 转换成 tuple 才能进行哈希
            mp[tuple(counts)].append(st)
        
        return list(mp.values())

但是更好地思路是利用素数：

from collections import defaultdict
class Solution:
    def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
        prime = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103]
        order = defaultdict(int)
        c = ord('a')
        for i in range(26):
            order[chr(c + i)] = prime[i]
        ans = defaultdict(list)
        for s in strs:
            tmp = 1
            for c in s:
                tmp *= order[c]
            print(tmp)
            ans[tmp].append(s)
        rst = []
        for a in ans:
            rst.append(ans[a])
        return rst

55. 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

维护一个能到达的最大值，
如果能到达的最大值可以到了n-1，就True。
如果i比maxloc还大，说明到不了i，就已经可以发现到不了n了，False
都不满足就继续往下走，更新maxloc

    def canJump(self, nums: List[int]) -> bool:
        if min(nums) > 0:
            return True
        maxloc = 0
        n = len(nums)
        for i in range(n):
            if maxloc >= n-1:
                return True
            
            if i > maxloc:
                return False
            maxloc = max(maxloc, i + nums[i])

56. 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

根据左区间排序之后，一个个放到ans中，如果ans的最后一个和目前的i有交集，就更新ans[-1][1]

    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x:x[0])
        ans = []
        for i in intervals:
            if len(ans) == 0 or i[0] > ans[-1][1]:
                ans.append([i[0], i[1]])
            elif i[0] < ans[-1][1]:
                ans[-1][1] = max(ans[-1][1], i[1])
        return ans

62. 不同路径 64. 最小路径和

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。

经典二维动归，不贴代码了
如果需要记录路径，需要对每个点记录方向(-1,-1)(-1,0)等

颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(nums)
        p0, p1 = 0, 0
        for i in range(n):
            if nums[i] == 1:
                nums[p1], nums[i] = nums[i], nums[p1]
                p1 += 1
            elif nums[i] == 0:
                nums[p0], nums[i] = nums[i], nums[p0]
                if p0 < p1:
                    nums[p1], nums[i] = nums[i], nums[p1]
                p1 += 1
                p0 += 1
        return nums

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

这道题本身没什么，递归或者迭代就能解决，但是需要注意到python对list对象是地址引用，所有每次给ans放值的时候都要深拷贝一下。
并且nowlist也要在append之后pop一下

from copy import deepcopy
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans = []
        def dfs(n, now, nowlist):
            if now == n:
               ans.append(deepcopy(nowlist))
            else:
                dfs(n, now+1, nowlist)
                nowlist.append(nums[now])
                dfs(n, now+1, nowlist)
                nowlist.pop()
        dfs(len(nums), 0, [])
        return ans 

96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
输入：n = 3 输出：5

第一种方式是下面的动态规划方法：

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0 for i in range(n+1)]
        dp[0] = 1
        dp[1] = 1
        for i in range(2, n+1):
            for j in range(0, i):
                dp[i] += dp[j] * dp[i-j-1]
        return dp[n]

第二种是利用数学原理：卡特兰数

class Solution(object):
    def numTrees(self, n):
        """
        :type n: int
        :rtype: int
        """
        C = 1
        for i in range(0, n):
            C = C * 2*(2*i+1)/(i+2)
        return int(C)

560. 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。
输入：nums = [1,1,1], k = 2
输出：2

利用前缀和和哈希表的思想：

from collections import defaultdict
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        pre = 0
        hashlist = defaultdict(int)
        ans = 0
        hashlist[0] = 1
        for n in nums:
            pre += n
            ans += hashlist[pre - k]
            # 最后更新hashlist[pre]是因为防止k==0的情况误加情况
            hashlist[pre] += 1
        return ans

309. 最佳买卖股票时机含冷冻期

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

f[i][0] 代表手中有股票的收益
f[i][1] 代表在i这里卖出股票的收益
f[i][2] 代表在i这里没有买入股票，并且手里也没有股票的收益

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.empty()){
            return 0;
        }
        int n = prices.size();
        vector<vector<int>> f(n, vector<int>(3));
        f[0][0] = -prices[0];
        for (int i = 1; i < n; i++){
            f[i][0] = max(f[i-1][0], f[i-1][2] - prices[i]);
            f[i][1] = f[i-1][0] + prices[i];
            f[i][2] = max(f[i-1][1], f[i-1][2]);
        }
    return max(f[n-1][1], f[n-1][2]);
    }
};

# 三、Hard
## 23. 合并K个升序链表

> 给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

抛弃朴素的方法
采用分治的方法
```python
class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if not lists:return 
        n = len(lists)
        return self.merge(lists, 0, n-1)


    def merge(self,lists, left, right):
        if left == right:
            return lists[left]
        mid = left + (right - left) // 2
        l1 = self.merge(lists, left, mid)
        l2 = self.merge(lists, mid+1, right)
        return self.mergeTwoLists(l1, l2)

        
    def mergeTwoLists(self,l1, l2):
        if not l1:return l2
        if not l2:return l1
        if l1.val < l2.val:
            l1.next = self.mergeTwoLists(l1.next, l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1, l2.next)
            return l2

32. 最长有效括号

给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。
输入：s = “)()())”
输出：4
解释：最长有效括号子串是 “()()”

左右两边分别扫描
如果遇到 left== right的时候，就是一种情况
从左向右的时候，如果right>left，left和right都变0
从右向左的时候，如果right

    def longestValidParentheses(self, s: str) -> int:
        left = 0
        right = 0
        ans = 0
        n = len(s)
        for c in s:
            if c == '(':
                left += 1
            else:
                right += 1
            if left == right:
                ans = max(ans, 2 * right)
            elif right > left:
                left = 0
                right = 0
        left = 0
        right = 0
        for i in range(n-1, -1, -1):
            c = s[i]
            if c == '(':
                left += 1
            else:
                right += 1
            if left == right:
                ans = max(ans, 2 * right)
            elif right < left:
                left = 0
                right = 0

        return ans

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

1. 动归可以作为第一解，进行两次扫描，记录每一个点的左右两边的最大值，每个点最多可以补水到min(left[i],right[i])

def trap(self, height: List[int]) -> int:
    n = len(height)
    left = [0 for i in range(n)]
    right = [0 for i in range(n)]
    for i in range(1, n):
        left[i] = max(left[i-1], height[i-1])
    for i in range(n-2, -1, -1):
        right[i] = max(right[i+1], height[i+1])
    ans = 0
    for i in range(1, n-1):
        tmp = min(left[i], right[i])
        if tmp > height[i]:
            ans += tmp - height[i]
    return ans

2. 通过上面的过程可以发现，每个点的加水量只和左右两边最高的两个支柱有关，所以利用双指针解决，O（N）时间复杂度

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        l = 0
        r = n-1
        left = 0
        right = 0
        ans = 0
        while l < r:
            left = max(left, height[l])
            right = max(right, height[r])
            # 假如height[l] < height[r] 一定有left <= right
            # 如果l=0,r=n-1,肯定两者的大小关系和height[l]，height[r]一样
            # 进而因为只有小的height才会向内缩进，所以一直会满足这个定理
            if height[l] < height[r]:
                ans += left - height[l] # left因为每次都max，所以一定>=height[left]的
                l += 1
            else:
                ans += right - height[r] # right同理
                r -= 1
        return ans

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

输入：heights = [2,1,5,6,2,3]
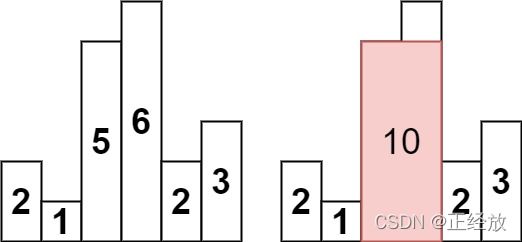
输出：10
解释：最大的矩形为图中红色区域，面积为 10

利用单调栈的理解实现如下：
需要注意的几个点在代码中标注了

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
    	# 左哨兵
        stack = [(-1,0)]
        # 右哨兵
        heights.append(0)
        n = len(heights)
        ans = 0
        for i in range(n):
        	# 不破坏单调性就直接放入
            if heights[i] >= stack[-1][1]:
                stack.append((i, heights[i]))
            else:
            	# 不断对栈中的数字进行判断和弹出，得到新的单调栈
                while stack[-1][1] > heights[i]:
                    x, y = stack[-1]
                    # 这里是对上面例子中读到2，
                    # 但是栈中有156的情况进行判断，
                    # 考虑这个例子：[2,1,2]就知道为什么要这么实现，
                    # 要考虑左哨兵
                    ans = max(ans, y*(i-stack[-2][0]-1))
                    stack.pop()
                stack.append((i, heights[i]))
		# 因为右哨兵的存在，所以一次循环就可以实现结果的计算
        return ans

72. 编辑距离（未完成）

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符 删除一个字符 替换一个字符

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

看下边的橙色的部分，这完全就是84题呀！

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        def largestRectangleArea(heights: List[int]) -> int:
            # 左哨兵
            stack = [(-1,0)]
            # 右哨兵
            heights.append(0)
            n = len(heights)
            ans = 0
            for i in range(n):
                # 不破坏单调性就直接放入
                if heights[i] >= stack[-1][1]:
                    stack.append((i, heights[i]))
                else:
                    # 不断对栈中的数字进行判断和弹出，得到新的单调栈
                    while stack[-1][1] > heights[i]:
                        x, y = stack[-1]
                        # 这里是对上面例子中读到2，
                        # 但是栈中有156的情况进行判断，
                        # 考虑这个例子：[2,1,2]就知道为什么要这么实现，
                        # 要考虑左哨兵
                        ans = max(ans, y*(i-stack[-2][0]-1))
                        stack.pop()
                    stack.append((i, heights[i]))
            # 因为右哨兵的存在，所以一次循环就可以实现结果的计算
            return ans
        ans = 0
        n = len(matrix)
        if n == 0:
            return 0
        m = len(matrix[0])
        high = [0 for i in range(m)]
        if m == 0:
            return 0
        for i in range(n):
            for j in range(m):
                if matrix[i][j] == '0':
                    high[j] = 0
                else:
                    high[j] += 1
            ans = max(ans, largestRectangleArea(high))
        
        return ans