2023 年牛客多校第九场题解

B Semi-Puzzle: Brain Storm

题意：给定 $a,m$，构造一个非负整数 $u$，使得 $a^u\equiv u(\mathrm{mod}m)$。$1\le a<m\le 10^9$，$0\le u\le 10^{18}$。多测，$1\le T\le 10^3$。

解法：首先定义记号 ${}^{\infty }a$ 表示 $a^{a^{a^{\cdots }}}$，即 $a$ 叠无穷多层指数塔。首先不难注意到一个最简单的性质：
$$a^{{}^{\infty }a}{=}^{\infty }a$$
这个数字显然是不可计算的无穷大，但是考虑在模意义下，由于模运算内参与运算的元素个数有限，并且由下面的扩展欧拉定理：
$$a^b\equiv \begin{array}{r}\{\begin{array}{ll}{a}^{b\mathrm{mod}\phi (m)},& \gcd (a,m)=1\\ a^b,& \gcd (a,m)\ne 1,b\le \phi (m)\\ a^{b\mathrm{mod}\phi (m)+\phi (m)},& \gcd (a,m)\ne 1,b>\phi (m)\end{array}\end{array}$$
这个 ${}^{\infty }a$ 一定在模意义下对应一个唯一确定的整数。下文中讨论 ${}^{\infty }a$ 的值，一定是针对于某个特定的模数而言。

由扩展欧拉定理可得，要想求 ${}^{\infty }a\mathrm{mod}m$，考虑使用扩展欧拉定理。显然 ${}^{\infty }a$ 充分大，因而有：
$${}^{\infty }a\equiv a^{{}^{\infty }a\mathrm{mod}\phi (m)+\phi (m)}(\mathrm{mod}m)$$
而对于任意一个数字 $m$，不断对它求 $\phi (m)$，不超过 $\mathcal{O}(2\log m)$ 次操作就可以使 $m=1$，这时 ${}^{\infty }a\equiv 0(\mathrm{mod}1)$，因而更高次指数不再有意义，因而可以通过下面的递归函数求出 ${}^{\infty }a\mathrm{mod}m$ 的值。本题即P4139 上帝与集合的正确用法。

long long dfs(long long base, long long p)
{
    if (p == 1)
        return 0;
    long long phip = phi(p);
    long long y = power(base, dfs(base, phip) + phip, p);
    return y;
}

下面开始对本题的正式解法描述。

法一：首先考虑 $a^u\equiv u(\mathrm{mod}m)$ 的形式。如果假设 $u$ 有 $a^k$ 形式，则带入可得 $a^{a^k}\equiv a^k(\mathrm{mod}m)$。如果这个 $u$ 充分大（即大于 $\phi (m)$），则根据扩展欧拉定理的指数条件有 $a^k\equiv k(\mathrm{mod}\phi (m))$，而这个式子与原式形式完全相同且模数减小，因而可以考虑一路递归下去，如此进行到 $m=1$。这时考虑边界条件，不妨设此时的 $u$ 仍然具有 $a^k$ 形式，而这显然成立（模 $1$ 意义下什么值都是 $0$）。因而，我们可以假定 $u$ 就是 ${}^{\infty }a$。

由于 ${}^{\infty }a$ 对于不同的模数就有不同的值，回到原式考虑这个 $u$ 需要满足什么条件。显然由最基本的条件，$a^{{}^{\infty }a}={}^{\infty }a\equiv u(\mathrm{mod}m)$。此外，由于它在指数上，因而由 $a^u\equiv {}^{\infty }a=a^{{}^{\infty }a}(\mathrm{mod}m)$ 可得 $u\equiv {}^{\infty }a(\mathrm{mod}\phi (m))$。注意这里的 $u$ 要充分大。因而可以得到如下的同余方程：
$$\{\begin{array}{l}u\equiv {}^{\infty }a(\mathrm{mod}m)\\ u\equiv {}^{\infty }a(\mathrm{mod}\phi (m))\end{array}$$
因而有 $u\equiv {}^{\infty }a(\mathrm{mod}\mathrm{lcm}(m,\phi (m)))$。考虑直接用上述方程组解 exCRT（扩展中国剩余定理）即可。因为 ${}^{\infty }a(\mathrm{mod}\mathrm{lcm}(\phi (m),m))$ 一定存在，因而上述同余方程组一定有解。复杂度 $\mathcal{O}\left(T\sqrt{V}\right)$。

#include 

using namespace std;
using ll = long long;
ll mul(ll a, ll b, ll p) {
    ll r = a * b - (ll)((long double)a / p * b + 0.5) * p;
    return r < 0 ? r + p : r;
}
ll fpow(ll a, ll b, ll p, ll x = 1) {
    for (; b; b >>= 1, a = mul(a, a, p))
        if (b & 1) x = mul(x, a, p);
    return x;
}
int phi(int x) {
    int p = x;
    for (int i = 2; i * i <= x; i++) {
        if (x % i) continue;
        p -= p / i;
        while (x % i == 0) x /= i;
    }
    if (x > 1) p -= p / x;
    return p;
}
int A;
ll f(ll x) {
    if (x == 1) return 1;
    ll p = phi(x), lcm = p * x / __gcd(p, x);
    return fpow(A, f(p), lcm) + lcm;
}
void Solve() {
    int x;
    scanf("%d%d", &A, &x);
    ll w = f(x), d = (ll)x * phi(x) / __gcd(x, phi(x));
    printf("%lld\n", w >= 1e18 ? w % d : w);
}
int main() {
    int t = 1;
    scanf("%d", &t);
    while (t--) Solve();
    return 0;
}

法二：首先不难注意到当 $\gcd (a,m)=1$ 时，$a^{\phi (m)}\equiv 1(\mathrm{mod}m)$。如果 $\phi (m)|u$ 且 $u\equiv 1(\mathrm{mod}m)$ 有解的时候这样的 $u$ 就是合法的。可惜这个同余方程组不一定有解。考虑让上述方程有解，即考虑一个一般情况，即 $u$ 仍然是充分大（大于 $\phi (m)$）时，有 $a^u\equiv a^c(\mathrm{mod}m)$，其中 $c$ 为一常数且 $c\in [\phi (m),2\phi (m))$。则考虑指数和底数条件有：
$$\begin{array}{rl}u& \equiv a^c(\mathrm{mod}m)\\ u& \equiv c(\mathrm{mod}\phi (m))\end{array}$$
消去 $u$ 将同余方程组转化为丢番图方程，观察对 $c$ 的约束，有：
$$a^c+k_{1}m=c+k_2\phi (m)$$
即 $a^c-c=k_{1}m+k_2\phi (m)$，右侧必为 $g=\gcd (m,\phi (m))$ 的倍数。由于 $k_1,k_2$ 的任意性，右侧可以组合出一切 $g$ 的倍数，因而有 $a^c\equiv c(\mathrm{mod}g)$，就可以开始递归计算上述方程 $c$ 的解。对于每一轮递归，可以考虑暴力回代解出相应的 $u$。

D Non-Puzzle: Error Permutation

题意：给定长度为 $n$ 的排列 $\{P{\}}_{i=1}^n$，问有多少个连续子区间 $[l,r]$，在区间中从左往右数的第 $i$ 个数字都不是该区间的第 $i$ 小。$ 1\le n \le 5\times 10^3$。

解法：反过来思考出现什么情况会让一个区间不合法。对于一个确定的数字 $P_i$，考虑对于区间 $[l,r]$，如果这个 $P_i$ 导致了区间不合法，那一定是它是这个区间的第 $i$ 小。考虑 $P_i$ 左侧比 $P_i$ 大的个数，和 $P_i$ 右侧比 $P_i$ 小的数字个数，显然这两个要相等：即把 $P_i$ 左侧比 $P_i$ 大的数字都用 $i$ 右侧比 $P_i$ 小的数字替换就可以实现 $P_i$ 左侧都比 $P_i$ 小，右侧都比 $P_i$ 大。即，左大等于右小。

这时考虑枚举 $i$，依次去维护当 $l$ 从 $i$ 向左侧移动时，比 $P_i$ 大的数字个数变化情况——它一定是一段区间 $[l_0,r_0]$ 上都是 $0$ 个数字比 $P_i$ 大，$l\in [l_1,r_1]$ 上都是只有 $1$ 个数字比 $P_i$ 大，依次类推；右侧当 $r$ 从 $i$ 开始向右移动时也是同理：$[l_0^{\prime },r_0^{\prime }]$ 都是 $0$ 个数字比 $P_i$ 小，$[l_1^{\prime },r_1^{\prime }]$ 都是 $1$ 个数字比 $P_i$ 小，等等。那么对于固定的 $i$，它将会导致整个二维矩阵区间 $[l_j,r_j]:[l_j^{\prime },r_j^{\prime }]$ 都变成不合法的。

初始化矩阵为全 $0$ 矩阵，每次出现不合法就直接对这个不合法矩阵区域整体加一，最后统计右上角矩阵中 $0$ 个数即为答案。而对于这种矩阵整体更新，就可以直接使用二维差分快速维护对于每个 $i$ 的 $\mathcal{O}(n)$ 次更新，最后前缀和即可。整体复杂度 $\mathcal{O}(n^2)$。

#include 
#define fp(i, a, b) for (int i = a, i##_ = int(b); i <= i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = int(b); i >= i##_; --i)

using namespace std;
using ll = long long;
const int N = 5e3 + 5;
int n, f[N][N], p[N];
vector<int> posy[N], posx[N];
void Solve() {
    scanf("%d", &n);
    fp(i, 1, n) scanf("%d", p + i);
    fp(i, 1, n) {
        int big = 0, small = 0;
        fp(r, i, n) {
            small += (p[r] < p[i]);
            posy[small].push_back(r);
        }
        fd(l, i, 1) {
            if (p[l] > p[i]) ++big;
            posx[big].push_back(l);
        }
        fp(j, 0, n)
            if (!posx[j].empty() && !posy[j].empty()) {
                f[posx[j].back()][posy[j].front()]++;
                f[posx[j].front() + 1][posy[j].front()]--;
                f[posx[j].back()][posy[j].back() + 1]--;
                f[posx[j].front() + 1][posy[j].back() + 1]++;
            }
        fp(j, 0, n) posx[j].clear(), posy[j].clear();
    }
    fp(i, 1, n) fp(j, 1, n) f[i][j] = (f[i][j] + f[i][j - 1] + f[i - 1][j] - f[i - 1][j - 1]);
    int ans = 0;
    fp(i, 1, n) fp(j, i, n) if (!f[i][j]) ++ans;
    printf("%d\n", ans);
}
void Clear() {
    fp(i, 0, n + 1) fp(j, 0, n + 1) f[i][j] = 0;
}
int main() {
    int t = 1;
    scanf("%d", &t);
    while (t--) Solve(), Clear();
    return 0;
}

E Puzzle: Square Jam

题意：给定 $n\times m$ 的矩形，将其划分成为若干个正方形，并且要求任何一个正方形的顶角不能和三个其他的正方形顶角重合（即划分出来的线不存在十字交叉）。输出一个构造方案。多测，$1\le T\le 10^5$，$1\le \sum n\times m\le 2\times 10^5$。

解法：本题和第四场 G 题非常相似——使用辗转相减法进行构造，每次裁剪最大的一个正方形即可。

#include 
#define fp(i, a, b) for (int i = a, i##_ = b; i <= i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = b; i >= i##_; --i)

using namespace std;
void Solve() {
    int a, b;
    scanf("%d%d", &a, &b);
    vector<array<int, 3>> ans;
    for (int x = 0, y = 0; a && b;) {
        if (a <= b) {
            fp(k, 0, b / a - 1)
                ans.push_back({x, y + k * a, a});
            y += b - b % a, b = b % a;
        } else {
            fp(k, 0, a / b - 1)
                ans.push_back({x + k * b, y, b});
            x += a - a % b, a = a % b;
        }
    }
    printf("YES\n%d\n", ans.size());
    for (auto [x, y, k] : ans)
        printf("%d %d %d\n", x, y, k);
}
int main() {
    int t = 1;
    scanf("%d", &t);
    while (t--) Solve();
    return 0;
}

G Non-Puzzle: Game

题意：给定长度为 $n$ 的序列 $\{a{\}}_{i=1}^n$，先后手轮流依次从序列中选择两个数字 $a_i,a_j$（可选相同数字）然后将 $a_i\oplus a_j$ 加入序列中。给定 $k$，谁先凑出 $k$ 谁获胜。问谁胜。$1\le n\le 10^6$，$0\le a_i,k<2^{30}$。

解法：考虑最后如果得到 $k$，那一定是由给出序列 $\{a{\}}_{i=1}^n$ 中的某几个元素异或起来得到的。因而我们只关心所得序列的数字种类而不关心每个数字具体有多少个。因而可以首先考虑对 $\{a\}$ 序列去重。下文中讨论的 $\{a\}$ 序列均无重复元素，设此时集合大小仍为 $n$。

首先最朴素的情况：如果当前先手一步操作就可以得到 $k$ 则先手必胜；从第二步操作开始，每个人都可以消极参赛——重复上一个人的操作，这样整个序列的数字种类数就不会发生变化，因而局面完全相同。因而不难得到，如果当前局面对于先手是必败的，则他一定会重复上一步操作让这个必败局面留给对手，进而达成平局。所以先手想要输，必须满足的条件是：

1. 先手没有上一步操作可以重复——即他在走第一步。
2. 先手走任意的操作，都会让后手一波操作获胜。否则先手可以考虑执行一步操作让后手没办法一步凑出 $k$。

因而不难发现如果游戏不能在两轮之内结束，双方就都会消极参赛。而后手必胜条件是先手无论操作什么，都能让他选出当前新的两个数字凑出 $k$（注意一定不可能是给定序列中的两个数字，因为这样会导致先手一波操作结束）。

因而后手必胜的充要条件是，$\forall i,j\in [1,n]$，$a_i\oplus a_j\ne k$，且 $\exists l\in [1,n]$，$a_i\oplus a_j\oplus a_l=k$。第一个条件可以通过哈希表枚举 $a_i$ 去查询 $k\oplus a_j$ 快速判断。对于第二个，利用异或性质可得 $(a_i\oplus k)\oplus (a_j\oplus k)=a_l\oplus k$。考虑 $a_i^{\prime }=a_i\oplus k$，定义集合 $A=\{x|x=a_i\oplus k\}$，则 $a_i^{\prime }\oplus a_j^{\prime }=a_l^{\prime }$ 对于任意的 $i,j$ 成立。因而 $a_i^{\prime }$ 集合在异或运算上封闭——即任取集合中的两个元素进行运算，其运算结果仍然在这个集合中。进而再推一步——从这个集合中选出任意多个元素进行异或运算，其运算结果仍然在这个集合 $A$ 中——每次进行一次两个集合内元素的异或运算，得到的结果仍然在集合中，就可以再次进行这样的异或运算。

因而只需要使用线性基判断出该集合对应的向量空间一定等于集合 $A$ 即可。而显然，集合 $A$ 一定在张成的向量空间中，因而只需要判断出该向量空间大小是否等于 $|A|$。而考虑由 $n$ 维的 $01$ 向量所张成空间的大小一定等于 $2^r$，其中 $r$ 为该矩阵的秩（主元个数）。而在向线性基插入元素的时候主元才会增加 $1$，因而统计这样的元素个数即可。

#include
using namespace std;
#define ll long long
ll read() {
	ll x=0, f=1; char ch=' ';
	while(!isdigit(ch)) { ch=getchar(); if(ch=='-') f=-1; }
	while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch-48), ch=getchar();
	return x*f;
}
ll d[70], cnt;
void insert(ll x) {
	for(int i=30;i>=0;i--) {
		if(x&(1ll<<i)) {
			if(!d[i]) {
				d[i]=x, cnt++;
				break;
				
			}
			else x^=d[i];
		}
	}
}
int t, n, k, a[1000005]; 
int main() {
	cin>>t;
	while(t--) {
		cin>>n>>k;
		for(int i=1;i<=n;i++) a[i]=read();
		map<int,int> mp;
		for(int i=1;i<=n;i++) {
			mp[k^a[i]]=1;
		}
		int ok=0;
		for(int i=1;i<=n;i++) {
			if(mp.count(a[i])) {
				cout<<"Alice"<<endl;
				ok=1;
				break;
			}
		}
		if(ok) continue;
		memset(d, 0, sizeof(d)), cnt=0;
		sort(a+1, a+n+1);
		n=unique(a+1, a+n+1)-a-1;
		for(int i=1;i<=n;i++) {
			insert(k^a[i]);
		}
		if(n==(1<<cnt)) cout<<"Bob"<<endl;
		else cout<<"Draw"<<endl;
	}
}

I Non-Puzzle: Segment Pair

题意：给定 $n$ 组区间，每组区间由两个区间构成。问从每组区间中选一个区间出来，这些区间能够同时覆盖同一个点的方案数。$1\le n\le 5\times 10^5$，区间数字范围 $[1,5\times 10^5]$。

解法：注意到区间覆盖的总长度只有 $5\times 10^5$，因而可以考虑枚举最终的这个全部覆盖点的位置，然后根据枚举区间从左到右依次插入或删除当前一对区间，观察和统计贡献。

但是根据覆盖点判断这样做可能有重复：如一对区间 $[1,3],[2,5]$，$2,3$ 都是被这一对区间包含，枚举 $2,3$ 的答案都是这一对区间中任意二选一，而实际上在 $2$ 或 $3$ 处进行二选一对应的方案是本质一样的。即当选择的最终点的位置不同时，每组区间的选法如果完全相同，此时应当视为同一种方案。为避免这一问题，可以考虑仅在每个区间开头处统计答案，即只在 $1,3$ 处统计答案。此时统计的答案因为新区间的开启必然会导致不同选法的出现。

考虑维护一个 $b$ 数组，随着全部覆盖点和区间的变化而实时更新。第 $i$（$i\in [0,2]$）项表示当前这个点被多少组区间覆盖 $i$ 次。例如区间 $[1,3],[2,5]$ 就让点 $2,3$ 被覆盖了两次，在覆盖点为 $2,3$ 时 $b_2$ 就因为这一组区间增大一，覆盖点为 $4,5$ 时则是 $b_1$ 被这组区间影响。那么随着覆盖点变化时，当 $b_0=0$ 即不存在一组区间在这个点上没有一次覆盖且满足是新区间开启条件时可以统计答案，答案即为 $2^{b_2}$，因为这 $b_2$ 组区间在当前点上都是两次覆盖，可以任选。

考虑如何维护这个 $b$ 数组——可以记录每组中每个区间开始和结束的位置，并用 $\{a{\}}_{i=1}^n$ 数组维护第 $i$ 组区间在当前点上已经覆盖了多少次。则对于第 $i$ 组中某个区间开始或结束，只需要更新 $b_{a_i}$ 加一或减一即可。总时间复杂度 $\mathcal{O}(n\log n)$，因为涉及对区间操作（开始或结束）位置的排序。

#include 
using namespace std;
const int N = 5e5 + 5, mod = 1e9 + 7;
int n, l1, r1, l2, r2, a[N], b[3], p[N];
struct node
{
    int x, y, id;
};
vector<node> ve;
bool cmp(node a, node b)
{
    if (a.x != b.x)
        return a.x < b.x;
    return a.y < b.y;
}
int main()
{
    cin >> n;
    p[0] = 1;
    for (int i = 1; i <= n; i++)
        p[i] = p[i - 1] * 2ll % mod;
    for (int i = 1; i <= n; i++)
    {
        cin >> l1 >> r1 >> l2 >> r2;
        ve.push_back({l1, 1, i});
        ve.push_back({r1 + 1, -1, i});
        ve.push_back({l2, 1, i});
        ve.push_back({r2 + 1, -1, i});
    }
    sort(ve.begin(), ve.end(), cmp);
    b[0] = n;
    long long ans = 0;
    for (auto v : ve)
    {
        b[a[v.id]]--;
        a[v.id] += v.y;
        if (v.y == 1 && !b[0])
            ans += p[b[2]], ans %= mod;
        b[a[v.id]]++;
    }
    cout << ans;
}

J Puzzle: Star Battle

题意：给定 $4n\times 4n$ 的正方形，该正方形划分为 $4n$ 个可能不连通的区域。要求每个区域内选出 $n$ 个点，使得这 $4n^2$ 个点在每行、每列上都有恰好 $n$ 个，且这些点互不八邻接。构造一个方案，或输出无解。$1\le n\le 300$。

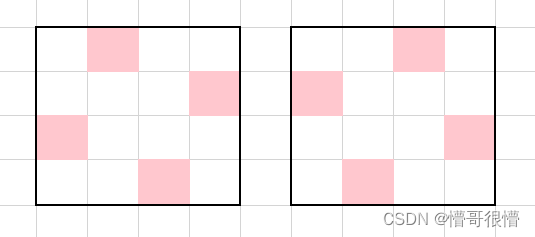
解法：首先考虑题目中要求边长都是 $4$ 的倍数的特殊用意。考虑下图中 $4\times 4$ 的构造方法，符合条件的仅有两种：

由于边长一定是 $4$ 的倍数，考虑按照 $4\times 4$ 的基本型组合出大的形状。仅以左图为例：

每次向外扩展 $2+2$ 格，就是把内层的格子复制一次。这样整个图形根据两种内核，就只有两种构造方式。因而直接判断这两种核是不是合法的即可。

#include 
using namespace std;
const int N = 5000;
int n, a[N + 5][N + 5], b[N + 5][N + 5], vis[N + 5];
bool check()
{
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (b[i][j])
            {
                if (vis[a[i][j]] >= n / 4)
                    return false;
                vis[a[i][j]]++;
            }
    bool flag = true;
    for (int i = 1; i <= n; i++)
        if (!a[i])
            flag = false;
    return flag;
}
int main()
{
    scanf("%d", &n);
    n <<= 2;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i += 2)
        for (int j = 1; j <= n; j += 2)
        {
            if (i <= n / 2 && j <= n / 2)
                b[i][j + 1] = 1;
            if (i <= n / 2 && j > n / 2)
                b[i + 1][j + 1] = 1;
            if (i > n / 2 && j <= n / 2)
                b[i][j] = 1;
            if (i > n / 2 && j > n / 2)
                b[i + 1][j] = 1;
        }
    if (check())
    {
        printf("YES\n");
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (b[i][j])
                    printf("%d %d\n", i, j);
        return 0;
    }
    for (int l = 1, r = n; l < r; l++, r--)
        for (int j = 1; j <= n; j++)
            swap(b[l][j], b[r][j]);
    if (check())
    {
            printf("YES\n");
            for (int i = 1; i <= n; i++)
                for (int j = 1; j <= n; j++)
                    if (b[i][j])
                        printf("%d %d\n", i, j);
            return 0;
        }
    printf("NO");
    return 0;
}