【算法系列篇】双指针
文章目录
- 前言
- 什么是双指针算法
- 1.移动零
-
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2.复写零
-
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3.快乐数
-
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4.盛最多水的容器
-
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 5.有效三角形的个数
-
- 5.1 题目要求
- 5.2 做题思路
- 5.3 Java代码实现
- 6.和为S的两个数字
-
- 6.1 题目要求
- 6.2 做题思路
- 6.3 Java代码实现
- 7.三数之和
-
- 7.1 题目要求
- 7.2 做题思路
- 7.3 Java代码实现
- 8.四数之和
-
- 8.1 题目要求
- 8.2 做题思路
- 8.3 Java代码实现
前言
朋友们,大家好啊,从今天开始我将陆续为大家更新关于算法方面的文章,如果大家对于算法感兴趣的话,欢迎大家订阅我的算法专栏。
什么是双指针算法
双指针算法(Two Pointers Algorithm)是一种常用的算法技巧,通常用于数组、链表或其他线性数据结构中的问题。该算法使用两个指针在数据结构上进行迭代、搜索或比较,以解决特定的问题。
在双指针算法中,通常使用两个指针分别称为"快指针"和"慢指针"。快指针和慢指针起始位置通常相同,然后根据问题的要求,以不同的步长移动指针。快指针可能会每次移动多个位置,而慢指针则每次只移动一个位置。
双指针算法有几种常见的应用方式:
-
对撞指针(Two Pointers Approach):快指针从数组的首部开始,慢指针从数组的尾部开始,两者向中间移动,直到它们相遇或交叉。这种方法通常用于有序数组中的搜索、求和等问题。
-
快慢指针(Fast and Slow Pointers):快指针和慢指针以不同的速度遍历链表。这种方法通常用于解决链表中的环检测、找到链表中点、链表的反转等问题。
-
滑动窗口(Sliding Window):使用两个指针在数组或字符串上定义一个固定大小的窗口,然后根据问题要求移动窗口的起始位置或结束位置。这种方法通常用于字符串或数组中的子串或子数组问题。
双指针算法的优点在于它的时间复杂度通常较低,并且在遍历数据时只需要常量级的额外空间。它可以有效地降低问题的时间复杂度,并且常常用于解决一些数组、链表相关的问题。
1.移动零
https://leetcode.cn/problems/move-zeroes/
1.1 题目要求
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
class Solution {
public void moveZeroes(int[] nums) {
}
}
1.2 做题思路
这个题目的目的就是将数组中的所有零给移动到非0数字的右边部分,而我们使用双指针就刚好可以将一个数组分为三部分,第一部分是非零部分,第二部分是数字0,第三部分是待移动的部分。
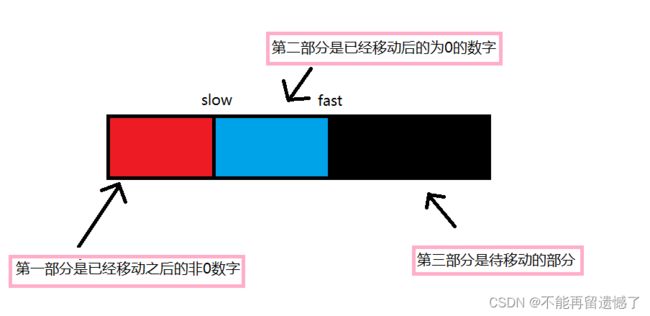
而这三个部分,我们使用两个指针 slow 和 fast 来维护,当 fast 所指的数字不为 0 时,就与 slow 所指的数字进行交换。这样就可以保证 slow 左边是已经移动之后的非 0 数字,slow 与 fast 之间是移动之后的 0 数字,fast 右边是待移动的部分。
1.3 Java代码实现
class Solution {
public void moveZeroes(int[] nums) {
int slow = -1;
int fast = 0;
int n = nums.length;
while(fast < n) {
if(nums[fast] != 0) {
int tmp = nums[++slow];
nums[slow] = nums[fast];
nums[fast] = tmp;
}
fast++;
}
}
}
2.复写零
https://leetcode.cn/problems/duplicate-zeros/
2.1 题目要求
给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:arr = [1,0,2,3,0,4,5,0]
输出:[1,0,0,2,3,0,0,4]
解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]
示例 2:
输入:arr = [1,2,3]
输出:[1,2,3]
解释:调用函数后,输入的数组将被修改为:[1,2,3]
class Solution {
public void duplicateZeros(int[] arr) {
}
}
2.2 做题思路
很多人拿到这个题首先想的是从前往后使用双指针,当遇到0的时候,将0写两次,但是如果这样的话会将后面的数字给覆盖,这就会显得很麻烦。我们不妨换个思路:可以先找到复写之后数组的最后一个数字,然后从后往前进行数据的写入,当遇到0就写两次,非0就写一次。
所以做这个题目大致分为两步:1.找到复写之后数组的最后一个数字 2.从后往前写入数据
2.3 Java代码实现
class Solution {
public void duplicateZeros(int[] arr) {
int slow = 0;
int fast = -1;
int n = arr.length;
//1.找到复写之后数组的最后一个数字
while(fast < n-1) {
if(arr[slow] != 0) fast++;
else fast += 2;
if(fast >= n-1) break;
slow++;
}
//2.调整边界
//当fast=n的时候,说明slow所指的最后一个数字为0
if(fast == n) {
arr[n-1] = 0;
fast = n-2;
slow--;
}
//3.从后往前写入数据
while(slow >= 0) {
if(arr[slow] != 0) {
arr[fast--] = arr[slow--];
}else {
arr[fast--] = 0;
arr[fast--] = 0;
slow--;
}
}
}
}
3.快乐数
https://leetcode.cn/problems/happy-number/
3.1 题目要求
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
class Solution {
public boolean isHappy(int n) {
}
}
3.2 做题思路
要判断是否为快乐数,我们需要知道,当我们进行每位数的平方和这个操作的时候,最终都会形成一个环。
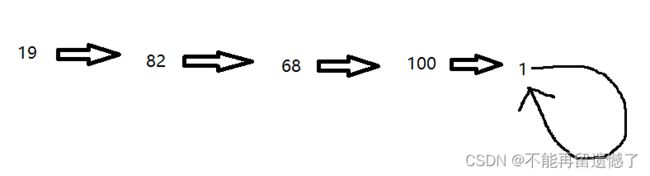

既然都会形成环,那么我们只需要使用快慢指针来找到这个环,然后判断这个环是否为1,如果是快乐数的话,他会在1->1之间形成环,而非快乐数就不一定了。
3.3 Java代码实现
class Solution {
private int bitSum(int n) {
int sum = 0;
while(n != 0) {
int tmp = n % 10;
sum += tmp*tmp;
n /= 10;
}
return sum;
}
public boolean isHappy(int n) {
int slow = n;
int fast = bitSum(n); //这里先将快指针进行一次求和操作,防止刚开始就相等了
//slow每次进行一次操作,fast一次进行两次操作
while(slow != fast) {
slow = bitSum(slow);
fast = bitSum(bitSum(fast));
if(slow == fast) break;
}
return slow == 1;
}
}
4.盛最多水的容器
https://leetcode.cn/problems/container-with-most-water/
4.1 题目要求
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
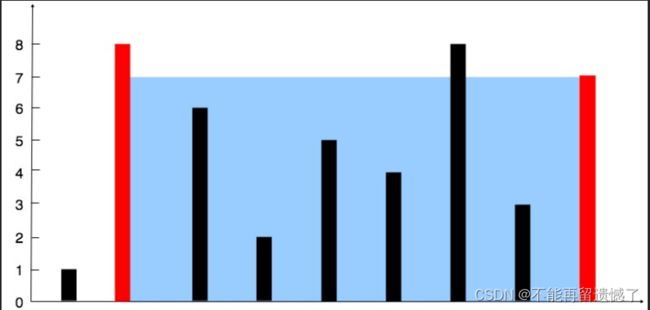
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
class Solution {
public int maxArea(int[] height) {
}
}
4.2 做题思路
容器的容量跟 xy 的乘积有关,所以我们既需要考虑 x,也需要考虑 y,但是无法保证一上来 x 和 y 就是最大的,我们只能保证 x 或者 y 其中一个是最大的,然后再找 xy 最大的时候。所以这里我们先保证 x 是最大的,left 指针指向最左边,right 指针指向最右边,接着再找 x*y 乘积最大。
容积这样计算 (right - left) * min(height[left],height[right])。设置一个变量来存放体积,并不断更新这个变量,保证这个变量存储的是容积最大的数据。left 和 right 的值也是需要不断改变的,需要更换掉 left 和 right 所指向的数据较小的指针,因为我们要找的是乘积最大的数据。
- 容器的宽度⼀定变⼩。
- 由于左边界较⼩,决定了⽔的⾼度。如果改变左边界,新的⽔⾯⾼度不确定,但是⼀定不会超过右边的柱⼦⾼度,因此容器的容积可能会增⼤。
- 如果改变右边界,⽆论右边界移动到哪⾥,新的⽔⾯的⾼度⼀定不会超过左边界,也就是不会超过现在的⽔⾯⾼度,但是由于容器的宽度减⼩,因此容器的容积⼀定会变⼩的
4.3 Java代码实现
class Solution {
public int maxArea(int[] height) {
int n = height.length;
int left = 0;
int right = n-1;
int ret = 0; //用来存储体积
while(left < right) {
int v = (right - left) * Math.min(height[left],height[right]);
ret = Math.max(v,ret);
if(height[left] < height[right]) left++;
else right--;
}
return ret;
}
}
5.有效三角形的个数
https://leetcode.cn/problems/valid-triangle-number/
5.1 题目要求
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
示例 2:
输入: nums = [4,2,3,4]
输出: 4
class Solution {
public int triangleNumber(int[] nums) {
}
}
5.2 做题思路
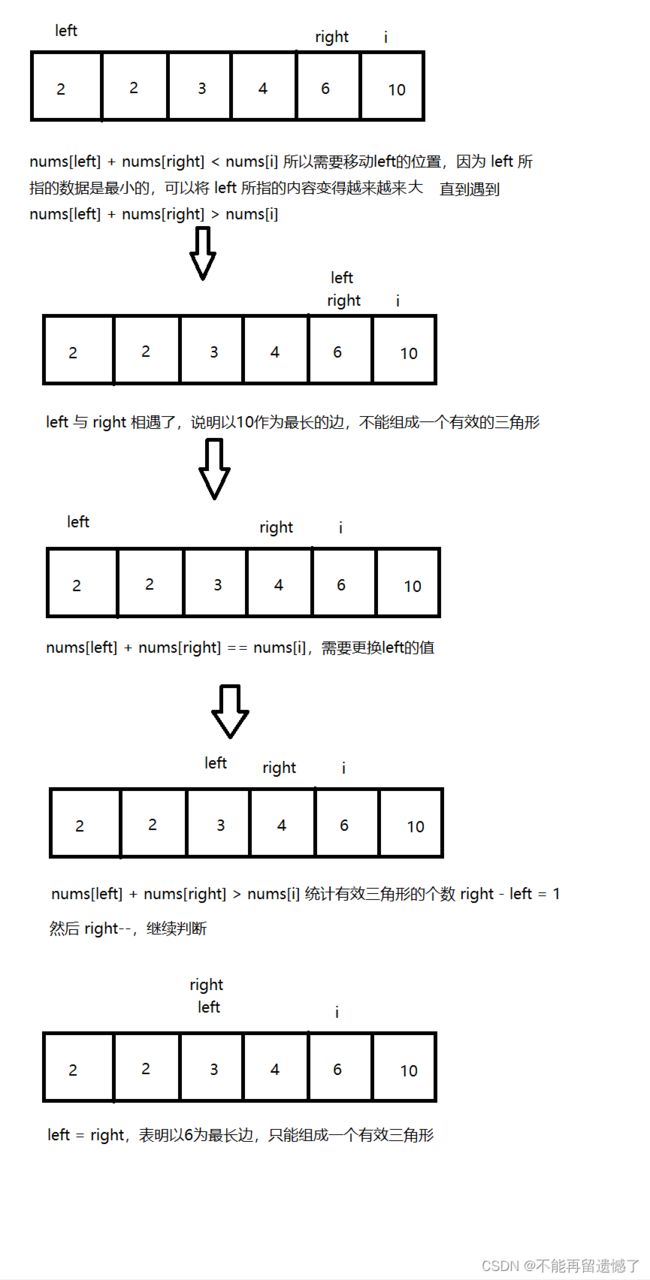
说的有效的三角形,大家应该都不陌生吧:任意两边之和大于第三边,但是,我们真的需要两两组合都判断一遍吗,其实并不是的,只需要判断两个较短的边之和大于较长的那个边就可以了。
既然知道了只需要判断一次就可以判断是否是有效的三角形,所以我们可以先对数组进行一个升序排序,从数组的最后开始,将它作为三角形的最长的边,然后在前面的数组范围内,left 指针指向前面部分的最左边,right 指针指向最右边,通过移动 left 和right 的位置来统计有效三角形的个数。如果 nums[left] + nums[right} > 最长的边,那么从 left 开始到 right - 1 的边和 right、最长的边都可以组合成一个有效的三角形;所以,以该长度为最长边的三角形的个数为 right -left,然后right–,继续该操作,直到left == right;如果 nums[left] + nums[right} < 最长的边,就需要移动 left 的位置,直到遇到 nums[left] + nums[right} > 最长的边 的位置,再统计有效三角形的个数。
5.3 Java代码实现
class Solution {
public int triangleNumber(int[] nums) {
Arrays.sort(nums);
int sum = 0;
for(int i = nums.length-1; i > 1; i--) {
int left = 0;
int right = i-1;
while(left < right) {
if(nums[left] + nums[right] > nums[i]) {
sum = sum + right - left;
right--;
}else {
left++;
}
}
}
return sum;
}
}
6.和为S的两个数字
https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/
6.1 题目要求
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[2,7] 或者 [7,2]
示例 2:
输入:nums = [10,26,30,31,47,60], target = 40
输出:[10,30] 或者 [30,10]
class Solution {
public int[] twoSum(int[] nums, int target) {
}
}
6.2 做题思路
这个题目的思路跟上面的思路差不多。使用双指针,left 指向数组的最左边(也就是最小值),right 指向数组的最右边(最大值),然后判断 nums[left] + nums[right] 跟target 的关系,如果 nums[left] + nums[right] > target ,就调整 right 的值;如果 nums[left] + nums[right] < target 就调整 left 的值,如果相等就存下来。
6.3 Java代码实现
class Solution {
public int[] twoSum(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left < right) {
int sum = nums[left] + nums[right];
if(sum > target) {
right--;
}else if(sum < target) {
left++;
}else {
return new int[]{nums[left],nums[right]};
}
}
return new int[]{-1,-1};
}
}
7.三数之和
https://leetcode.cn/problems/3sum/
7.1 题目要求
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
}
}
7.2 做题思路
当直到了如何解决两数之和的问题之后,求三数值和其实也很简单,还是现将数组以升序的方式排序我们每次固定一个数字,然后在剩下的数组中找到和为 target - nums[i] 的值,但是真的有这么简单吗?注意看题目,答案中不可出现重复的三元组,什么叫做重复的三元组,看第一个示例,它等于 target 的三个数有 (-1,0,1),(0,1,-1),(-1,2,-1) ,但是最终输出的结果只有[[-1,-1,2],[-1,0,1]],所以这道题关键难在去重这个问题上,那么我们应该如何去重呢?当调整 left、right 和那个固定的数字的时候,如果所指的数字等于前面的数字那么就跳过。
7.3 Java代码实现
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
int n = nums.length;
int i = 0;
while(i < n && nums[i] <= 0) {
int left = i + 1;
int right = n - 1;
int target = -nums[i];
while(left < right) {
int sum = nums[left] + nums[right];
if(sum > target) {
right--;
}else if(sum < target) {
left++;
}else {
List<Integer> list1 = new ArrayList<>();
list1.add(nums[i]);
list1.add(nums[left]);
list1.add(nums[right]);
list.add(list1);
left++;
right--;
//去重并且防止越界
while(left < right && nums[left] == nums[left-1]) left++;
while(left < right && nums[right] == nums[right+1]) right--;
}
}
i++;
while(i < n && nums[i] <= 0 && nums[i] == nums[i-1]) i++;
}
return list;
}
}
8.四数之和
https://leetcode.cn/problems/4sum/
8.1 题目要求
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例 2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
}
}
8.2 做题思路
这个求四数之和,如果前面的两数之和和三数之和会做了,这个题目也很简单,我们只需要先固定一个数字,然后在后面的数组内找到和为 target - nums[i] 的三个数就行了,唯一需要注意的就是去重。那么这个题目我就不过多介绍了,大家直接看代码就行了。
8.3 Java代码实现
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list = new ArrayList<>();
int i = 0;
int n = nums.length;
Arrays.sort(nums);
while(i < n) {
int j = i + 1;
long tmp1 = target-nums[i];
while(j < n) {
int slow = j + 1;
int fast = n-1;
long tmp2 = tmp1 - nums[j];
while(slow < fast) {
int sum = nums[slow] + nums[fast];
if(sum > tmp2) {
fast--;
}else if(sum < tmp2) {
slow++;
}else {
List<Integer> list1 = new ArrayList<>();
list1.add(nums[i]);
list1.add(nums[j]);
list1.add(nums[slow]);
list1.add(nums[fast]);
list.add(list1);
slow++;
fast--;
while(slow < fast && nums[slow] == nums[slow-1]) slow++;
while(slow < fast && nums[fast] == nums[fast+1]) fast--;
}
}
j++;
while(j < n && nums[j] == nums[j-1]) j++;
}
i++;
while(i < n && nums[i] == nums[i-1]) i++;
}
return list;
}
}