05有监督学习——神经网络
-
线性模型
给定n维输入: x = [ x 1 , x 1 , … , x n ] T x = {[{x_1},{x_1}, \ldots ,{x_n}]^T} x=[x1,x1,…,xn]T
线性模型有一个n维权重和一个标量偏差: w = [ w 1 , w 1 , … , w n ] T , b w = {[{w_1},{w_1}, \ldots ,{w_n}]^T},b w=[w1,w1,…,wn]T,b
输出是输入的加权和: y = w 1 x 1 + w 2 x 2 + … + w n x n + b y = {w_1}{x_1} + {w_2}{x_2} + \ldots + {w_n}{x_n} + b y=w1x1+w2x2+…+wnxn+b,向量表示: y = < w , x > + b y = < w,x > + b y=<w,x>+b
1.1 广义线性模型
除了直接让模型预测值逼近实值标记y,我们还可以让它逼近y的衍生物,这就是广义线性模型(generalized linear model)
y = g − 1 ( w T x + b ) y = {g^{ - 1}}({w^T}x + b) y=g−1(wTx+b)
其中 g(.)称为联系函数(link function),要求单调可微。使用广义线性模型我们可以实现强大的非线性函数映射功能。比方说对数线性回归(log-linear regression),令g(.) = In(.),此时模型预测值对应的是真实值标记在指数尺度上的变化。
1.2 Sigmoid函数
σ ( z ) \sigma (z) σ(z) 代表一个常用的逻辑函数(logistic function)为S形函数(Sigmoid function),则:
σ ( z ) = g ( z ) = 1 1 + e − z , z = w T x + b \sigma (z) = g(z) = {1 \over {1 + {e^{ - z}}}},z = {w^T}x + b σ(z)=g(z)=1+e−z1,z=wTx+b
合起来,我们得到的逻辑回归模型的假设函数:
L ( y ^ , y ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) \mathrm{L}(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y}) L(y^,y)=−ylog(y^)−(1−y)log(1−y^) -
分类与回归
-
感知机模型
单层感知机数学模型: y = f ( ∑ i = 1 N w i x i + b ) y = f(\sum\limits_{i = 1}^N {{w_i}{x_i}} + b) y=f(i=1∑Nwixi+b)
其中,f称为激活函数
1986年,Rumelhart和McClIelland为首的科学家提出了BP( Back Propagation )神经网络的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,目前是应用最广泛的神经网络。
3.1 训练数据
-
收集一些数据点来决定参数值(权重和偏差),例如过去6个月卖的房子。这被称之为训练数据·通常越多越好假设我们有n个样本,记
x = [ x 1 , x 1 , … , x n ] T x = {[{x_1},{x_1}, \ldots ,{x_n}]^T} x=[x1,x1,…,xn]T, y = [ y 1 , y 1 , … , y n ] T y = {[{y_1},{y_1}, \ldots ,{y_n}]^T} y=[y1,y1,…,yn]T3.2衡量预估质量
比较真实值和预估值,例如房屋售价和估价
假设y是真实值, y ^ \hat y y^是估计值,我们可以比较:
ℓ ( y , y ^ ) = 1 2 ( y − y ^ ) 2 \ell(y, \hat{y})=\frac{1}{2}(y-\hat{y})^2 ℓ(y,y^)=21(y−y^)2
这个叫做平方损失
训练损失:
ℓ ( X , y , w , b ) = 1 2 n ∑ i = 1 n ( y i − ⟨ x i , w ⟩ − b ) 2 = 1 2 n ∥ y − X w − b ∥ 2 \ell(\mathbf{X}, \mathbf{y}, \mathbf{w}, b)=\frac{1}{2 n} \sum_{i=1}^n\left(y_i-\left\langle\mathbf{x}_i, \mathbf{w}\right\rangle-b\right)^2=\frac{1}{2 n}\|\mathbf{y}-\mathbf{X} \mathbf{w}-b\|^2 ℓ(X,y,w,b)=2n1i=1∑n(yi−⟨xi,w⟩−b)2=2n1∥y−Xw−b∥2
最小化损失来学习参数:
w ∗ , b ∗ = arg min w , b ℓ ( X , y , w , b ) \mathbf{w}^*, \mathbf{b}^*=\arg \min _{\mathbf{w}, b} \ell(\mathbf{X}, \mathbf{y}, \mathbf{w}, b) w∗,b∗=argw,bminℓ(X,y,w,b)3.3 梯度下降
- 挑选一个初始值 w 0 {w_0} w0
- 重复迭代参数t=1,2,3
w t = w t − 1 − η ∂ ℓ ∂ w t − 1 {w_t} = {w_{t - 1}} - \eta {{\partial \ell } \over {\partial {w_{t - 1}}}} wt=wt−1−η∂wt−1∂ℓ - 沿梯度方向将增加损失函数值
- 学习率:步长的超参数
优点:
1.能够自适应、自主学习。BP可以根据预设参数更新规则,通过不断调整神经网络中的参数,已达到最符合期望的输出。
2.拥有很强的非线性映射能力。
3.误差的反向传播采用的是成熟的链式法则,推导过程严谨且科学。
4.算法泛化能力很强。
缺点:
1.BP神经网络参数众多,每次迭代需要更新较多数量的阈值和权值,故收敛速度比较慢。
2.网络中隐层含有的节点数目没有明确的准则,需要不断设置节点数字试凑,根据网络误差
结果最终确定隐层节点个数
3.BP算法是一种速度较快的梯度下降算法,容易陷入局部极小值的问题。
-
激活函数
在深度学习模型中,我们一般习惯在每层神经网络的计算结果送入下一层神经网络之前先经过一个激活函数。
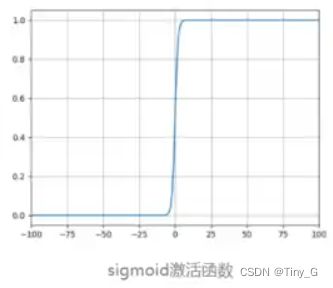
(1)Sigmod函数: f ( x ) = 1 1 + e − x f(x) = {1 \over {1 + {{\rm{e}}^{ - x}}}} f(x)=1+e−x1
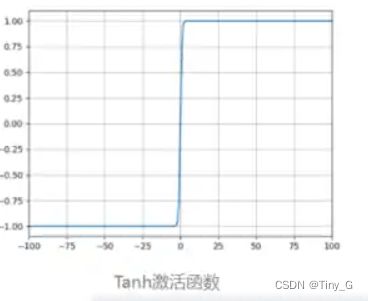
(2)Tanh函数: tanh ( x ) = e x − e − x ( e x + e − x ) = 2 ∗ s i g m o d ( 2 x ) − 1 \tanh (x) = {{{e^x} - {e^{ - x}}} \over {({e^x} + {e^{ - x}})}} = 2*sig\bmod (2x) - 1 tanh(x)=(ex+e−x)ex−e−x=2∗sigmod(2x)−1
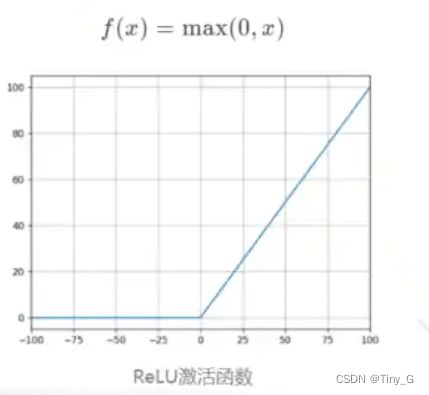
(3)relu函数: f ( x ) = max ( 0 , x ) f(x) = \max (0,x) f(x)=max(0,x)
-
维度诅咒
神经网络模型可以非常方便地对数据进行升降维,随着特征数量的增多,样本的密度就下降了,继续升维度,就会过拟合,不适用于真实情况
-
欠拟合与过拟合
过拟合和欠拟合可以通过训练误差和泛化误差来定义:
训练误差:模型在训练集上 计算得到的误差泛化误差:模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望。过拟合:模型的训练误差小,泛化误差大欠拟合:模型的训练误差和泛化误差都大过拟合的处理方法:
(1) 正则化:正则化的,但是减少参数的大小,它可以改善或者减少过拟合问题
(2) 数据增强: 数据的质量、数量和难度等进行增强
(3)降维: 即丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,也可以使用一些模型选择的算法来帮忙。
(4)集成学习方法: 集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险。过拟合的处理方法:
(1)添加新特征
(2)增加模型复杂度
(3)减小正则化系数 -
正则
深度学习中的正则可以看作通过约束模型复杂度来防止过拟合现象的一些手段。首先,模型复杂度是由模型的参数量大小和参数的可取值范围一起决定的。因此正则方法也大致分为两个方向:
一个方向致力于约束模型参数量,例如Dropout;
一个方向致力于约束模型参数的取值范围,例如weight decay。
权重衰减方法:
(1)使用均方范数作为硬性限制
通过限制参数值的选择范围来控制模型容量:
min ℓ ( w , b ) \min \ell (w,b) minℓ(w,b)subject to ∥ w ∥ 2 ≤ θ {\left\| {\rm{w}} \right\|^2} \le \theta ∥w∥2≤θ
通常不限制b
(2)使用均方范数作为柔性限制
对于每个 θ \theta θ,都可以找到 λ \lambda λ,使得之前的目标函数等价于下面式子:
min ℓ ( w , b ) + λ 2 ∥ w ∥ 2 \min \ell (w,b) + {\lambda \over 2}{\left\| w \right\|^2} minℓ(w,b)+2λ∥w∥2
超参数 λ \lambda λ控制了正则项的重要程度:
- λ \lambda λ = 0 无作用
- λ → ∞ , w ∗ → 0 \lambda \to \infty ,w* \to 0 λ→∞,w∗→0
-
数据增强
-
数值稳定性
这种数值不稳定性问题再深度学习训练过程中被称作梯度消失和梯度爆炸。
梯度消失:由于累乘导致的梯度接近0的现象,此时训练没有进展。
梯度爆炸:由于累乘导致计算结果超出数据类型能记录的数据范围,导致报错。防止出现数值不稳定原因的方法是进行数据归一化处理。
数据归一化处理:
(1)归一化(最大-最小规范化)——将数据映射到【0,1】区间
x ∗ = x − x min x max − x min x* = {{x - {x_{\min }}} \over {{x_{\max }} - {x_{\min }}}} x∗=xmax−xminx−xmin
数据归一化的目的是使得各特征对目标变量的影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
(2)Z-Score标准化——处理后的数据均 值为0,方差为1
x ∗ = x − μ σ x* = {{x - \mu } \over \sigma } x∗=σx−μ
数据标准化为了不同特征之间具备可比性,经过标准化变换之后的特征数据分布没有发生改变。
就是当数据特征取值范围或单位差异较大时,最好是做一下标准化处理。
-
神经网络大家族
- CNN
- RNN
- 句法语义分析
- 信息检索
- 自动文摘
- 文本数据挖掘
- 自动问答
- 机器翻译
- 知识图谱
- 情感分析
- 文本相似度
- 文本纠错
- GNN
- 芯片设计
- 场景分析与问题推理
- 推荐系统(用户画像)
- 欺诈检测与风控相关
- 知识图谱
- 道路交通的流量预测
- 自动驾驶(无人机等场景)
- 化学,医疗等场景
- 生物,制药等场景
- 社交网络
- GAN
- 图像超分辨率
- 艺术创作
- 图像到图像的翻译(风格迁移)
- 文本到图像的翻译
- 照片编辑
- 服装翻译
- 照片到表情符号
- 照片融合
- 照片修补