多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测

多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测

预测效果

基本介绍

1.SCNGO-CNN-Attention超前24步多变量回归预测算法。
程序平台：无Attention适用于MATLAB 2020版及以上版本；融合Attention要求Matlab2023版以上；
2.基于融合正余弦和折射反向学习的北方苍鹰优化算法（SCNGO）、卷积神经网络（CNN）融合注意力机制的超前24步多变量时间序列回归预测算法；
3.北方苍鹰优化算法（Northern Goshawk Optimization，NGO）由MOHAMMAD DEHGHANI等人于2022年提出，该算法，该算法模拟了北方苍鹰捕猎过程（猎物识别和攻击、追逐及逃生）；
4.多变量特征输入，单序列变量输出，输入前一天的特征，实现后一天的预测，超前24步预测；
5.改进策略参照麻雀优化算法，改进点如下：
①采用折射反向学习策略初始化北方苍鹰算法个体，基本思想是通过计算当前解的反向解来扩大搜索范围，借此找出给定问题更好的备选解；
②采用正余弦策略替换原始苍鹰算法的勘察阶段的位置更新公式；
③对正余弦策略的步长搜索因子进行改进；原始步长搜索因子呈线性递减趋势，不利于进一步平衡北方苍鹰算法的全局搜索和局部开发能力。
6.多变量特征输入，单序列变量输出，输入前一天的特征，实现后一天的预测，超前24步预测；
7.通过SCNGO优化算法优化学习率、卷积核大小、卷积核个数，这3个关键参数，以最小MAPE为目标函数；
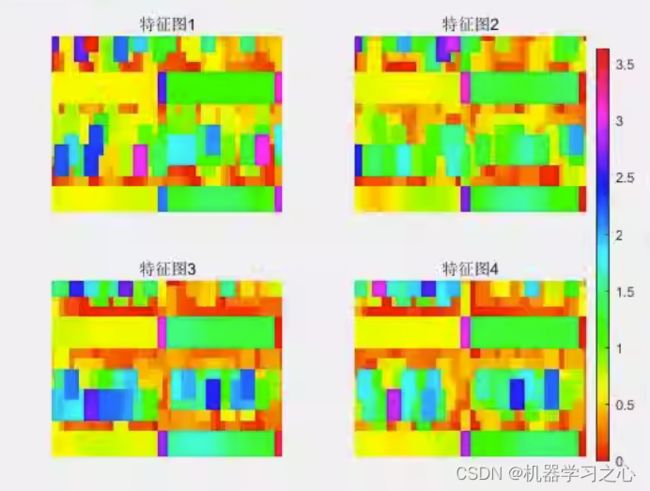
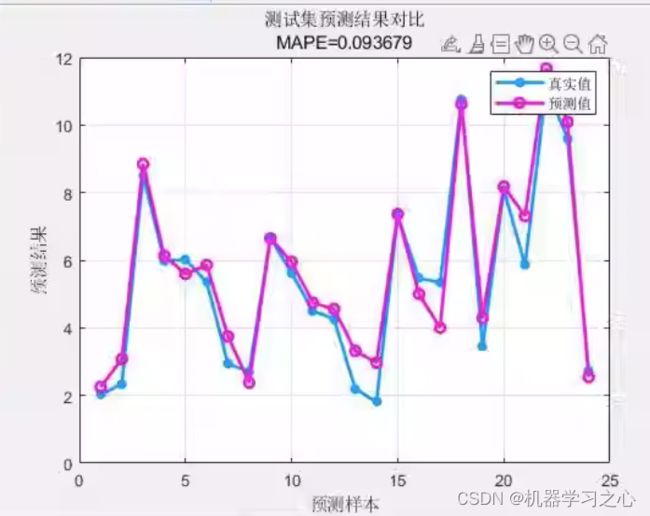
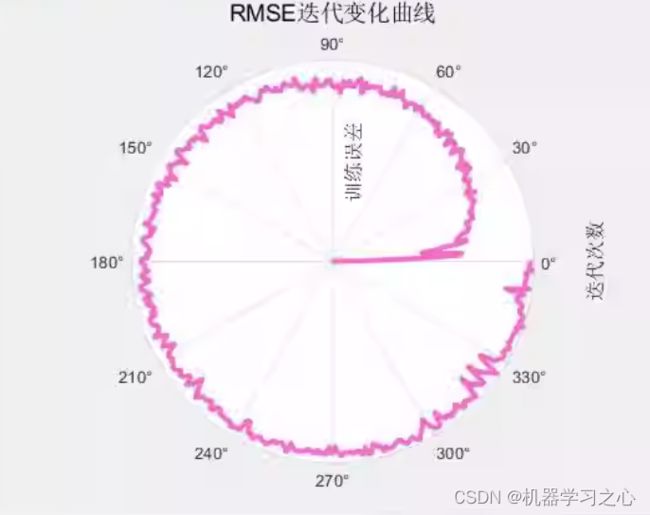
8.提供损失、RMSE迭代变化极坐标图；网络的特征可视化图；测试对比图；适应度曲线；
7.提供MAPE、RMSE、MAE等计算结果展示。
适用领域：
风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。
使用便捷：
直接使用EXCEL表格导入数据，无需大幅修改程序。内部有详细注释，易于理解。

程序设计

• 完整源码和数据获取方式：私信博主回复MATLAB实现SCNGO-CNN-Attention多变量时间序列预测；

lgraph = connectLayers(lgraph, "seqfold/out", "conv_1");             % 折叠层输出 连接 卷积层输入
lgraph = connectLayers(lgraph, "seqfold/miniBatchSize", "sequnfold/miniBatchSize"); 
                                                                     % 折叠层输出连接反折叠层输入
lgraph = connectLayers(lgraph, "relu_2", "sequnfold/in");            % 激活层输出 连接 反折叠层输入
lgraph = connectLayers(lgraph, "sequnfold", "flip");
lgraph = connectLayers(lgraph, "bigru2", "cat/in2");

%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法
    'MaxEpochs', 100,...                  % 最大训练次数
    'MiniBatchSize',64,...                % 批处理
    'InitialLearnRate', 0.001,...         % 初始学习率为0.001
    'L2Regularization', 0.001,...         % L2正则化参数
    'LearnRateSchedule', 'piecewise',...  % 学习率下降
    'LearnRateDropFactor', 0.1,...        % 学习率下降因子 0.1
    'LearnRateDropPeriod', 400,...        % 经过800次训练后 学习率为 0.001*0.1
    'Shuffle', 'every-epoch',...          % 每次训练打乱数据集
    'ValidationPatience', Inf,...         % 关闭验证
    'Plots', 'training-progress',...      % 画出曲线
    'Verbose', false);

%%  训练模型
[net,traininfo] = trainNetwork(p_train, t_train, lgraph, options);

%% 预测
t_sim1 = predict(net, p_train); 
t_sim2 = predict(net, p_test ); 

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);


%%  相关指标计算
%  R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

%  MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1')./T_train));
MAPE2 = mean(abs((T_test - T_sim2')./T_test));

disp(['训练集数据的MAPE为：', num2str(MAPE1)])
disp(['测试集数据的MAPE为：', num2str(MAPE2)])

%  MBE
mbe1 = sum(abs(T_sim1' - T_train)) ./ M ;
mbe2 = sum(abs(T_sim1' - T_train)) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%均方误差 MSE
mse1 = sum((T_sim1' - T_train).^2)./M;
mse2 = sum((T_sim2' - T_test).^2)./N;

disp(['训练集数据的MSE为：', num2str(mse1)])
disp(['测试集数据的MSE为：', num2str(mse2)])

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501