Day-03关于dp的一些题（笔记）

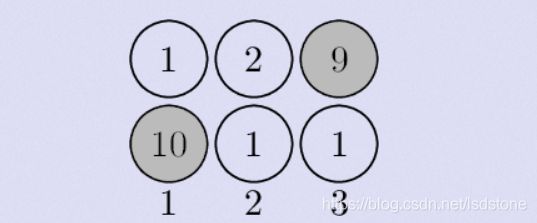
B - The Triangle

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

(Figure 1)
Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.

Sample Input

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Sample Output

30

• 思路：根据dp可从下至上求得最大值也可从上至下求得最大值。第一种形式采用从底向上，每一步从下边一个和下边一个的右一个，向上逐步递推，终点在第一排，另一种则是向下逐步递推。

AC代码如下（两种形式）：

#include
#include
using namespace std;
int dp[105][105];
int a[110][110];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= i; j++)
		{

			cin >> a[i][j];
	

		}
	}

	for (int i = n; i >= 1; i--)
	{

		for (int j = 1; j <= i; j++)
		{ 
			dp[i][j] = max(dp[i+1][j], dp[i +1][j+1]) + a[i][j];
		}
	}

	cout << dp[1][1] << endl;

		return 0;
}

#include
#include
using namespace std;
int dp[105][105];
int a[110][110];
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= i; j++)
		{
			cin >> a[i][j];
			dp[i][j] = max(dp[i-1][j], dp[i-1 ][j-1]) + a[i][j];	
		}	
	}

	int max1 = 0;
	for (int i = 1; i <= n; i++)
	{
		max1 = max(max1, dp[n][i]);

	}

	cout << max1;
	return 0;
}

C - Basketball Exercise

Finally, a basketball court has been opened in SIS, so Demid has decided to hold a basketball exercise session. 2⋅n2⋅n students have come to Demid’s exercise session, and he lined up them into two rows of the same size (there are exactly nn people in each row). Students are numbered from 11 to nn in each row in order from left to right.

Now Demid wants to choose a team to play basketball. He will choose players from left to right, and the index of each chosen player (excluding the first one) will be strictly greater than the index of the previously chosen player. To avoid giving preference to one of the rows, Demid chooses students in such a way that no consecutive chosen students belong to the same row. The first student can be chosen among all 2n2n students (there are no additional constraints), and a team can consist of any number of students.

Demid thinks, that in order to compose a perfect team, he should choose students in such a way, that the total height of all chosen students is maximum possible. Help Demid to find the maximum possible total height of players in a team he can choose.

Input
The first line of the input contains a single integer nn (1≤n≤1051≤n≤105) — the number of students in each row.

The second line of the input contains nn integers h1,1,h1,2,…,h1,nh1,1,h1,2,…,h1,n (1≤h1,i≤1091≤h1,i≤109), where h1,ih1,i is the height of the ii-th student in the first row.

The third line of the input contains nn integers h2,1,h2,2,…,h2,nh2,1,h2,2,…,h2,n (1≤h2,i≤1091≤h2,i≤109), where h2,ih2,i is the height of the ii-th student in the second row.

Output
Print a single integer — the maximum possible total height of players in a team Demid can choose.

Examples

Input

5
9 3 5 7 3
5 8 1 4 5

Output

29

Input

3
1 2 9
10 1 1

Output

19

Input

1
7
4

Output

7

Note

In the first example Demid can choose the following team as follows:

In the second example Demid can choose the following team as follows:

思路分析：根据题意可以推出一个递推公式，dp[i] [0]表示应该选第二行前两个中最大的那个max(dp[i - 1][1], dp[i - 2][1])来求得第二行的最大值并加上a[i],dp[i][1]表示应该选第一行当前元素所对应的前两个中最大的那一个max(dp[i - 1][0], dp[i - 2][0])并加上b[i]。再将得到的最大值保存在dp[i][2]中，得到最后的结论。

AC代码如下：

#include 
#include 
#include 
#include 
#define MAX 100005
using namespace std;
int n;
long long a[MAX], b[MAX], dp[MAX][3];
int main()
{
	cin >> n;

	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++)
		cin >> b[i];
	dp[1][0] = a[1];
	dp[1][1] = b[1];
	dp[1][2] = max(a[1], b[1]);
	for (int i = 2; i <= n; i++)
	{
		dp[i][0] = max(dp[i - 1][1], dp[i - 2][1]) + a[i];
		dp[i][1] = max(dp[i - 1][0], dp[i - 2][0]) + b[i];
		dp[i][2] = max(dp[i][0], dp[i][1]);
	}
	cout << dp[n][2] << endl;
	return 0;

}

D - QAQ

“QAQ” is a word to denote an expression of crying. Imagine “Q” as eyes with tears and “A” as a mouth.

Now Diamond has given Bort a string consisting of only uppercase English letters of length n. There is a great number of “QAQ” in the string (Diamond is so cute!).

illustration by 猫屋 https://twitter.com/nekoyaliu
Bort wants to know how many subsequences “QAQ” are in the string Diamond has given. Note that the letters “QAQ” don’t have to be consecutive, but the order of letters should be exact.

Input

The only line contains a string of length n (1 ≤ n ≤ 100). It’s guaranteed that the string only contains uppercase English letters.

Output

Print a single integer — the number of subsequences “QAQ” in the string.

Examples

Input

QAQAQYSYIOIWIN

Output

4

Input

QAQQQZZYNOIWIN

Output

3

Note

In the first example there are 4 subsequences “QAQ”: “QAQAQYSYIOIWIN”, “QAQAQYSYIOIWIN”, “QAQAQYSYIOIWIN”, “QAQAQYSYIOIWIN”.

解题思路：本题因为字符串长度较小可用暴力法依次遍历求解。

AC代码如下：

#include
using namespace std;

int main()
{
	char a[105];
	cin >> a;
	int count = 0;
	int len = strlen(a);

	for (int i = 0; i < len; i++)
	{
		for (int j = i + 1; j < len; j++)
		{

			for (int x = j + 1; x < len; x++)
			{

				if (a[i] == 'Q'&&a[j] == 'A'&&a[x] == 'Q')
					count++;

			}
		}
	}
	cout << count << endl;

	return 0;
}

G - WOW Factor

Recall that string aa is a subsequence of a string bb if aa can be obtained from bb by deletion of several (possibly zero or all) characters. For example, for the string aa=“wowwo”, the following strings are subsequences: “wowwo”, “wowo”, “oo”, “wow”, “”, and others, but the following are not subsequences: “owoo”, “owwwo”, “ooo”.

The wow factor of a string is the number of its subsequences equal to the word “wow”. Bob wants to write a string that has a large wow factor. However, the “w” key on his keyboard is broken, so he types two "v"s instead.

Little did he realise that he may have introduced more "w"s than he thought. Consider for instance the string “ww”. Bob would type it as “vvvv”, but this string actually contains three occurrences of “w”:

“vvvv”
“vvvv”
“vvvv”
For example, the wow factor of the word “vvvovvv” equals to four because there are four wows:

“vvvovvv”
“vvvovvv”
“vvvovvv”
“vvvovvv”
Note that the subsequence “vvvovvv” does not count towards the wow factor, as the "v"s have to be consecutive.

For a given string ss, compute and output its wow factor. Note that it is not guaranteed that it is possible to get ss from another string replacing “w” with “vv”. For example, ss can be equal to “vov”.

Input

The input contains a single non-empty string ss, consisting only of characters “v” and “o”. The length of ss is at most 106106.

Output

Output a single integer, the wow factor of ss.

Examples

Input

vvvovvv

Output

4

Input

vvovooovovvovoovoovvvvovovvvov

Output

100
Note
The first example is explained in the legend.

解题思路：在本题中两个v可看成一个w,我们要找wow的因子，就可以先去找到两个v然后再找一个o，再找到两个v，依次循环就可以得出wow的因子个数了。每次找到保存其前面已经找到的合，最后结束输出就是它的因子个数了。

AC代码如下：

#include
#include
using namespace std;
int main()
{	
	char a[1000005];
	cin >> a;
	long long  x = 0, y = 0, q = 0;
		int len = strlen(a);
		for (int i = 0; i < len-1; i++)
		{
			if (a[i] == a[i + 1] && a[i] == 'v'&&a[i + 1] == 'v')
			{
				x += y;
				q++;

			}

			if (a[i] == 'o')
			{
				y += q; 
				 
			}
		}

		cout << x << endl;

		return 0;
}

H - Letter

Patrick has just finished writing a message to his sweetheart Stacey when he noticed that the message didn’t look fancy. Patrick was nervous while writing the message, so some of the letters there were lowercase and some of them were uppercase.

Patrick believes that a message is fancy if any uppercase letter stands to the left of any lowercase one. In other words, this rule describes the strings where first go zero or more uppercase letters, and then — zero or more lowercase letters.

To make the message fancy, Patrick can erase some letter and add the same letter in the same place in the opposite case (that is, he can replace an uppercase letter with the lowercase one and vice versa). Patrick got interested in the following question: what minimum number of actions do we need to make a message fancy? Changing a letter’s case in the message counts as one action. Patrick cannot perform any other actions.

Input

The only line of the input contains a non-empty string consisting of uppercase and lowercase letters. The string’s length does not exceed 105.

Output

Print a single number — the least number of actions needed to make the message fancy.

Examples

Input

PRuvetSTAaYA

Output

5

Input

OYPROSTIYAOPECHATALSYAPRIVETSTASYA

Output

0

Input

helloworld

Output

0

解题思路：本题就是给定一个包含字母大小写的字符串，要求串的前面大写，串的后面小写。要把串的某个位置的前面全改为大写或串的后面全改为小写，求最小的修改次数。则就是用动态规划依次保存其修改的次数，最后再比较出一个最小值即可。

AC代码如下：

#include
#include
#include
using namespace std;
const int maxn = 1e5 + 5;
int a[maxn], b[maxn];
char s[100050];
int dp[100050][2];

int main()
	{

	cin >> s;
	int len = strlen(s);

	for (int i = 0; i < len; i++)
	{
		if (islower(s[i]))//如果是小写字母
		{
			dp[i][0] = min(dp[i - 1][0], dp[i-1][1]);
			dp[i][1] = dp[i - 1][1] + 1;//改变为大写的次数加一
		}

		else{
			dp[i][0] = min(dp[i - 1][0], dp[i-1][1]) + 1;//如果为大写则记录改变为小写时的次数
			dp[i][1] = dp[i - 1][1];
		}
	}

	cout << min(dp[len-1][0], dp[len-1][1]) << endl;


	return 0;
}