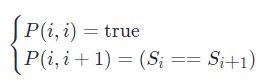leetcode-动态规划
通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
目录
5. 最长回文字串
10. 正则表达式匹配
22. 括号生成
32. 最长有效括号
42. 接雨水
44. 通配符匹配
45. 跳跃游戏ii
53. 最大子数组和
55. 跳跃游戏
62. 不同路径
63. 不同路径ii
64. 最小路径和
5. 最长回文字串
![]()
如果一个子串是回文串,那么它首尾两个字母去除之后仍然是个回文串,用P(i,j)表示字符串s第i个字母到第j个字母组成的串是否为回文串:
因此动态规划的转移方程为:
设置动态规划的边界条件:长度为1的子串一定是回文串,长度为2的子串当两个字母相同时为回文串。
从长度较短的字符串向长度较长的字符串进行转移。
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
n = len(s)
if n < 2:
return s
if n == 2:
if s[0] == s[1]:
return s
else:
return ""
max_len = 1
begin = 0
# 初始化状态转移矩阵,dp[i][j]表示s[i:j+1]是否为回文串
dp = [[False for _ in range(n)] for _ in range(n)]
for i in range(n):
dp[i][i] = True
# 枚举子串长度,从更短的子串开始循环
for L in range(2, n+1):
# 枚举左边界
for left in range(n):
right = left + L - 1
if right > n-1:
break
if s[left] != s[right]:
dp[left][right] = False
else:
dp[left][right] = dp[left+1][right-1]
if dp[left][right] and L > max_len:
max_len = L
begin = left
return s[begin: begin+max_len]第二种方法:枚举子串中心向外扩展
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
start, end = 0, 0
def expandAroundCenter(s, left, right):
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1
right += 1
return left + 1, right - 1
for center in range(len(s)):
left1, right1 = expandAroundCenter(s, center, center)
left2, right2 = expandAroundCenter(s, center, center + 1)
if right1 - left1 > end - start:
start, end = left1, right1
if right2 - left2 > end - start:
start, end = left2, right2
return s[start: end + 1]10. 正则表达式匹配
p中的一个字符只能匹配s中一个字符,匹配具有唯一性;
p中的一个字符+“*”可以匹配s中任意个字符,不具有唯一性;
因此考虑使用动态规划堆匹配的方案进行枚举,用f[i][j]表示s的前i个字符与p中的前j个字符是否匹配:
s[i] = p[j-1]即s末尾的字符匹配星号前面的字符
s[i] ≠ p[j-1]即丢掉星号和星号前面的字符,尝试匹配前面一串字符
class Solution(object):
def isMatch(self, s, p):
"""
:type s: str
:type p: str
:rtype: bool
"""
s_len, p_len = len(s), len(p)
# 检测s[i-1]与p[j-1]是否匹配
def isMatch(i, j):
if i == 0:
return False
if p[j - 1] == '.':
return True
return s[i - 1] == p[j - 1]
# dp[i][j]代表s[:i]与p[:j]是否匹配
dp = [[False] * (p_len + 1) for _ in range(s_len + 1)]
dp[0][0] = True # 空字符串自动匹配
for i in range(s_len + 1):
for j in range(1, p_len + 1):
if p[j - 1] == '*':
if isMatch(i, j - 1):
dp[i][j] = dp[i][j - 2] | dp[i - 1][j]
else:
dp[i][j] = dp[i][j - 2]
else: # 当s[i]与p[j]匹配时,s[:i]与p[:j]是否匹配取决于dp[i-1][j-1]
if isMatch(i, j):
dp[i][j] = dp[i - 1][j - 1]
return dp[s_len][p_len]22. 括号生成
当知道n个括号的所有组合以后,求n+1个括号只要往n个括号的结果中插入一对括号即可,插入的过程中保证’(‘’)‘的顺序,并使用set()去重:
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
res = ["()"]
if n == 1:
return res
def insertpar(res):
npath = len(res)
npar = len(res[0])
ans = []
for i in range(npath):
for left in range(npar):
for right in range(left+1, npar+2):
tmp = list(res[i])
tmp.insert(left, '(')
tmp.insert(right, ')')
ans.append(''.join(tmp))
return ans
while n > 1:
res = insertpar(res)
res = list(set(res))
n -= 1
return res组装法:
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
if n == 1:
return list({'()'})
res = set()
for i in self.generateParenthesis(n - 1):
for j in range(len(i) + 2):
res.add(i[0:j] + '()' + i[j:])
return list(res)已知i < n时括号所有排列,对于i = n的情况,假设新加进来的左括号在最左边,那么之前的所有括号要么在新括号里面,要么在新括号右面:
p + q = n - 1
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
if n == 0:
return []
total_l = [[None], ["()"]]
for i in range(2, n + 1): # 开始计算i组括号时的括号组合
l = []
for p in range(i): # 开始遍历 p q ,其中p+q=i-1 , p 作为索引
q = i - 1 - p
now_list1 = total_l[p]
now_list2 = total_l[q]
for k1 in now_list1:
for k2 in now_list2:
if not k1:
k1 = ""
if not k2:
k2 = ""
tmp = "(" + k1 + ")" + k2
l.append(tmp) # 把所有可能的情况添加到 l 中
total_l.append(l) # l这个list就是i组括号的所有情况,添加到total_l中,继续求解i=i+1的情况
return total_l[n]32. 最长有效括号
![]()
# 暴力解法,超时
class Solution(object):
def longestValidParentheses(self, s):
"""
:type s: str
:rtype: int
"""
max_length = 0
def isright(s):
stack = []
for i in s:
if i == '(':
stack.append('(')
else:
if not stack:
return False
stack.pop()
if stack:
return False
return True
for left in range(len(s) - 1):
if s[left] == ')':
continue
for right in range(left + 1, len(s)):
if s[right] == '(':
continue
if isright(s[left: right + 1]):
max_length = max(max_length, right - left + 1)
return max_length动态规划:dp[i]表示以i结尾的最长有效括号的长度,s[i]=='(' 时 dp[i]=0
如果字符串形如 “......))" i - dp[i-1] - 1如果是“)”则前面必没有有效字符(想使“)”有效则前面必有一个与之对应的“(”,那样dp[i-1]的值就应该更大)
class Solution(object):
def longestValidParentheses(self, s):
"""
:type s: str
:rtype: int
"""
n = len(s)
if n == 0:
return 0
# dp[i]为以i结尾的最长有效括号的长度
dp = [0 for _ in range(n)]
for index in range(1, n):
if s[index] == '(':
continue
if s[index-1] == '(' and s[index] == ')':
if index > 1:
dp[index] = dp[index-2] + 2
else:
dp[index] = 2
if s[index-1] == ')' and s[index] == ')':
if index-dp[index-1] > 0:
if s[index-dp[index-1]-1] == '(':
dp[index] = dp[index-1] + dp[index-dp[index-1]-2] + 2
return max(dp)42. 接雨水
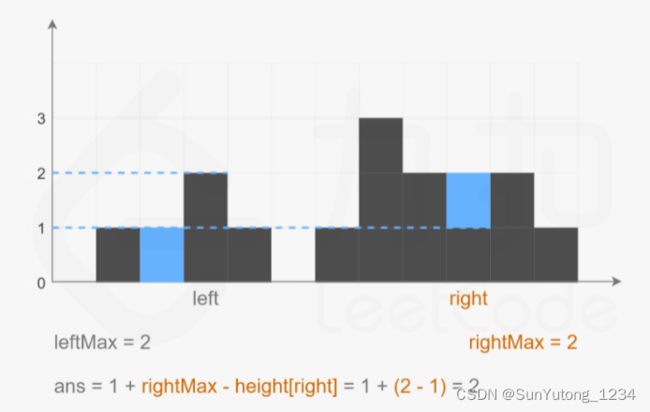
方法一:动态规划,维护两个数组leftMax和rightMax,记录下标i左边和右边的最大高度。
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
n = len(height)
leftMax = [0 for _ in range(n)]
leftMax[0] = height[0]
rightMax = [0 for _ in range(n)]
rightMax[n-1] = height[n-1]
n = len(height)
for i in range(1, n):
leftMax[i] = max(height[i], leftMax[i-1])
for i in range(n-2, -1, -1):
rightMax[i] = max(height[i], rightMax[i+1])
ans = 0
for i in range(n):
ans += min(leftMax[i], rightMax[i]) - height[i]
return ans方法二:单调栈
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
ans = 0
stack = []
for i, h in enumerate(height):
while stack and h > height[stack[-1]]:
top = stack.pop()
if not stack:
break
left = stack[-1]
curWidth = i - left - 1
curHeight = min(height[left], height[i]) - height[top]
ans += curWidth * curHeight
stack.append(i)
return ans方法三:双指针
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
ans = 0
left, right = 0, len(height) - 1
leftMax, rightMax = 0, 0
while left < right:
leftMax = max(leftMax, height[left])
rightMax = max(rightMax, height[right])
if height[left] < height[right]:
ans += leftMax - height[left]
left += 1
else:
ans += rightMax - height[right]
right -= 1
return ans44. 通配符匹配
class Solution(object):
def isMatch(self, s, p):
"""
:type s: str
:type p: str
:rtype: bool
"""
m, n = len(s), len(p)
# m+1 行 n+1 列,dp[i][j]表示s[i]与p[j]是否匹配
dp = [[False for _ in range(n+1)] for _ in range(m+1)]
dp[0][0] = True
for j in range(1, n+1):
if p[j-1] == '*':
dp[0][j] = True
else:
break
for i in range(1, m+1):
for j in range(1, n+1):
if p[j-1] == '*':
dp[i][j] = dp[i-1][j] | dp[i][j-1]
elif p[j-1] == '?' or s[i-1] == p[j-1]:
dp[i][j] = dp[i-1][j-1]
return dp[m][n]45. 跳跃游戏ii
class Solution(object):
def jump(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)-1
i = 0
count = 0
while i <= n:
if i == n :
return count
if i + nums[i] < n:
maxrange = i + nums[i] + nums[i + nums[i]]
tmp = nums[i]
for step in range(1, nums[i]+1):
twostep = i + step + nums[i+step]
if twostep > maxrange:
maxrange = twostep
tmp = step
i += tmp
count += 1
else:
count += 1
return count53. 最大子数组和
计算以当前下标为结束的最大连续子数组和dp[i]
dp[i] = max(dp[i-1] + nums[i], nums[i])
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
dp = [0 for _ in range(len(nums))]
dp[0] = nums[0]
for i in range(1, len(nums)):
dp[i] = max(dp[i-1] + nums[i], nums[i])
return max(dp)55. 跳跃游戏
class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
n = len(nums)
maxrange = 0
for i in range(n):
if i <= maxrange:
maxrange = max(maxrange, i+nums[i])
if maxrange >= n-1:
return True
return False62. 不同路径
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
dp = [[0 for _ in range(n)] for _ in range(m)]
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[m-1][n-1]63. 不同路径ii
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
n = len(obstacleGrid)
m = len(obstacleGrid[0])
d = {}
def dfs(i, j):
if (i,j) in d:
return d[i,j]
#边界/障碍物检查
if i >= n or j >= m or obstacleGrid[i][j] == 1:
return 0
#达到重点了
if i == n - 1 and j == m - 1:
return 1
#继续往右(i,j+1)、往下(i+1,j)递归调用
d[i,j] = dfs(i + 1, j) + dfs(i, j + 1)
return d[i,j]
return dfs(0, 0)64. 最小路径和
class Solution(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
n_row, n_col = len(grid), len(grid[0])
dp = [[0 for _ in range(n_col)] for _ in range(n_row)]
dp[0][0] = grid[0][0]
for i in range(1, n_row):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n_col):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1, n_row):
for j in range(1, n_col):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
return dp[n_row-1][n_col-1]