Cocos2d-x 3D渲染技术 （二）

3D坐标系统

五个空间

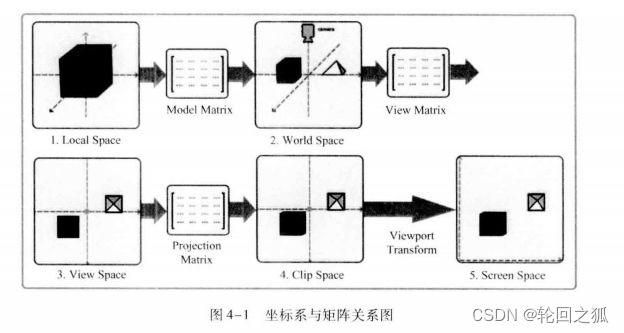
要把游戏模型显示到屏幕需要经历五个空间。

1. 局部空间 （Local Space，模型空间）
2. 世界空间 （Wolrd Space，游戏空间）
3. 观察空间 （View Space，视觉空间）
4. 裁剪空间 （Clip Space）
5. 屏幕空间 （Screen Space）

局部空间 （Local Space）

指模型对象所在的坐标空间，即建模软件的空间。

一般在导出创建的模型时，将模型的的坐标设为（0，0，0），目的是为了保持和世界坐标重合，方便调整其在世界坐标中的位置。

世界空间 （Wolrd Space）

游戏所在的场景就是世界空间。

将模型放到世界空间之后，可以对模型对象进行平移，缩放，旋转等操作，本质上就是通过矩阵的转换算法实现的。（模型举证）

观察空间 （View Space）

通过虚拟摄像机观察世界空间。

在游戏中，可以操作视角看到周围的物体。本质就是操作虚拟摄像机，将视线内的物体转换到摄像机的坐标系中。

观察空间也就是摄像机所观察的空间，是将物体对象的世界空间坐标转换为观察视觉内的坐标。

观察空间的计算需要使用观察矩阵

裁剪空间（Clip Space）

不能将所有的物体都移动到观察空间中，没有在视线范围内的物体需要被裁剪掉。

平截头体：由投影矩阵创建的观察区域。出现在其区域内的物体都会出现在屏幕中。

将场景中的物体从观察空间转换到裁剪空间，需要定义投影矩阵。

将一定范围内的坐标转化到标准设备坐标系的过程叫投影。

两种投影矩阵：

1. 正交投影矩阵 ======> 正交投影
2. 透视投影矩阵 ======> 透视投影

正交投影

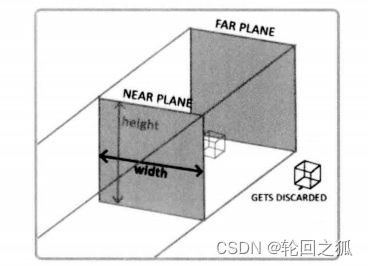
正交投影矩阵定义了一个类似立方体的平截头体。在立方体外的物体都会被裁剪掉。

在创建一个正交投影矩阵的时候，需要指定平截头体的宽度、高度和长度的远近。

摄像机的可视坐标系由这个平截头体的宽、高、深来决定。

由此可以看到，正交投影的矩阵由宽和高来决定，和深度无关。即不管远近，所显示的部分和近裁剪面是一致的。

作用：由于正交投影没有远近之分，一般作用于UI的摄像机上。

bool Camera::initOrthographic(float zoomX, float zoomY, float nearPlane, float farPlane)
{
    _zoom[0] = zoomX;
    _zoom[1] = zoomY;
    _nearPlane = nearPlane;
    _farPlane = farPlane;
    Mat4::createOrthographicOffCenter(0, _zoom[0], 0, _zoom[1], _nearPlane, _farPlane, &_projection);
    _viewProjectionDirty = true;
    _frustumDirty = true;
    _type = Type::ORTHOGRAPHIC;
    
    return true;
}

zoomX ： 平截头体的宽

zoomY ： 平截头体的高

nearPlane ：近裁剪面

farPlane ： 远裁剪面

然后调用函数createOrthographicOffCenter

void Mat4::createOrthographicOffCenter(float left, float right, float bottom, float top,
                                         float zNearPlane, float zFarPlane, Mat4* dst)
{
    GP_ASSERT(dst);
    GP_ASSERT(right != left);
    GP_ASSERT(top != bottom);
    GP_ASSERT(zFarPlane != zNearPlane);

    memset(dst, 0, MATRIX_SIZE);
    dst->m[0] = 2 / (right - left);
    dst->m[5] = 2 / (top - bottom);
    dst->m[10] = 2 / (zNearPlane - zFarPlane);

    dst->m[12] = (left + right) / (left - right);
    dst->m[13] = (top + bottom) / (bottom - top);
    dst->m[14] = (zNearPlane + zFarPlane) / (zNearPlane - zFarPlane);
    dst->m[15] = 1;
}

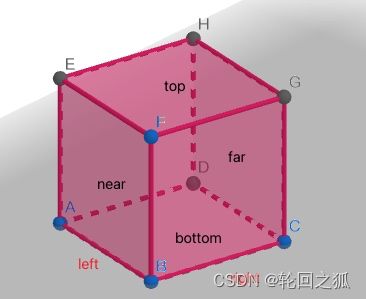
正交投影的平截头体为一个长方体[left,right][bottom,top][far,near]

那么需要把这个长方体转换到[-1,1][-1,1][-1,1]中

那么就需要两步。

平移

算出上面的长方体的中心点。

``[(left+right) / 2,(bottom+top) / 2,(far+near) / 2] ``

那么将这个点移动到原点。

平移公式为：

$$\left|\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& T_y\\ 0& 0& 1& T_z\\ 0& 0& 0& 1\end{array}\right|\cdot \left\{\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right\}=\left\{\begin{array}{c}{x}_1\\ y_1\\ z_1\\ 1\end{array}\right\}$$

其中 x1,y1,z1为新移动的点。

那么就可以得到，平移矩阵为

$$T^{-1}(t)=T(-t)=\left|\begin{array}{cccc}1& 0& 0& -T_x\\ 0& 1& 0& -T_y\\ 0& 0& 1& -T_z\\ 0& 0& 0& 1\end{array}\right|$$

所以，该长方体的平移矩阵为：

$$M_{translate}=\left|\begin{array}{cccc}1& 0& 0& -\frac{left+right}{2}\\ 0& 1& 0& -\frac{bottom+top}{2}\\ 0& 0& 1& -\frac{far+near}{2}\\ 0& 0& 0& 1\end{array}\right|$$

缩放

设缩放因子为s，则沿着坐标轴的缩放变换矩阵为：

$$S(s)=S(s_x,s_y,s_z)=\left|\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right|$$

缩放矩阵的逆为：

$$S^{-1}(s)=S(\frac{1}{s_x},\frac{1}{s_y},\frac{1}{s_z})=\left|\begin{array}{cccc}\frac{1}{s_x}& 0& 0& 0\\ 0& \frac{1}{s_y}& 0& 0\\ 0& 0& \frac{1}{s_z}& 0\\ 0& 0& 0& 1\end{array}\right|$$

要将$$[left,right]$$缩放到$$[-1,1]$$,那么它的缩放因子就为 $$\frac{2}{right-left}$$。

所以，该长方体的缩放变换矩阵为：

$$M_{scale}=\left|\begin{array}{cccc}\frac{2}{right-left}& 0& 0& 0\\ 0& \frac{2}{top-bottom}& 0& 0\\ 0& 0& \frac{2}{near-far}& 0\\ 0& 0& 0& 1\end{array}\right|$$

最后的正交投影矩阵就为：

$$Mortho=M_{scale}\ast M_{translate}$$

即：

$$M_{Orthographic}=\left|\begin{array}{cccc}\frac{2}{right-left}& 0& 0& 0\\ 0& \frac{2}{top-bottom}& 0& 0\\ 0& 0& \frac{2}{near-far}& 0\\ 0& 0& 0& 1\end{array}\right|\ast \left|\begin{array}{cccc}1& 0& 0& -\frac{left+right}{2}\\ 0& 1& 0& -\frac{bottom+top}{2}\\ 0& 0& 1& -\frac{far+near}{2}\\ 0& 0& 0& 1\end{array}\right|$$

起作用就是将正交投影的物体变换成标准视体。

这里保持一个疑惑 ：cocos2dx的代码中，矩阵最后的数不是算出来的。由于知识有限，不明白为啥那么写。即：

dst->m[12] = (left + right) / (left - right);
dst->m[13] = (top + bottom) / (bottom - top);
dst->m[14] = (zNearPlane + zFarPlane) / (zNearPlane - zFarPlane);

所以正交投影一般用在UI上。

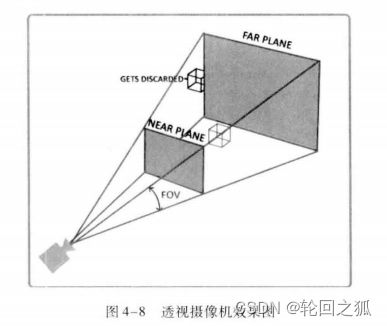
透视投影

它的特点是近大远小。这跟我们的眼睛是一样的。

Near Plane ： 近裁剪面
Far Plane ：远裁剪面
FOV ：视口的夹角

因为有远近之分，所以一般运用于3D场景中。

bool Camera::initPerspective(float fieldOfView, float aspectRatio, float nearPlane, float farPlane)
{
    _fieldOfView = fieldOfView;
    _aspectRatio = aspectRatio;
    _nearPlane = nearPlane;
    _farPlane = farPlane;
    Mat4::createPerspective(_fieldOfView, _aspectRatio, _nearPlane, _farPlane, &_projection);
    _viewProjectionDirty = true;
    _frustumDirty = true;
    _type = Type::PERSPECTIVE;
    
    return true;
}

fieldOfView : 即FOV，视野的夹角
aspectRatio ：屏幕视口的宽高比
nearPlane ： 近裁剪面
farPlane ：远裁剪面

创建透视投影矩阵的函数：

void Mat4::createPerspective(float fieldOfView, float aspectRatio,
                                     float zNearPlane, float zFarPlane, Mat4* dst)
{
    GP_ASSERT(dst);
    GP_ASSERT(zFarPlane != zNearPlane);

    float f_n = 1.0f / (zFarPlane - zNearPlane);
    float theta = MATH_DEG_TO_RAD(fieldOfView) * 0.5f;
    if (std::abs(std::fmod(theta, MATH_PIOVER2)) < MATH_EPSILON)
    {
        CCLOGERROR("Invalid field of view value (%f) causes attempted calculation tan(%f), which is undefined.", fieldOfView, theta);
        return;
    }
    float divisor = std::tan(theta);
    GP_ASSERT(divisor);
    float factor = 1.0f / divisor;

    memset(dst, 0, MATRIX_SIZE);

    GP_ASSERT(aspectRatio);
    dst->m[0] = (1.0f / aspectRatio) * factor;
    dst->m[5] = factor;
    dst->m[10] = (-(zFarPlane + zNearPlane)) * f_n;
    dst->m[11] = -1.0f;
    dst->m[14] = -2.0f * zFarPlane * zNearPlane * f_n;
}

需要把视锥体压缩成长方体，有三个原则：

1. near plane上的所有坐标不变
2. far plane上的所有点坐标的z值不变，都是far
3. far plane的中心点不变，即永远为(0,0,far)

$$M_{press}$$的推算方法，就是要找到一个使得下面的成立。

$$\left|\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right|=>\left|\begin{array}{c}nx/z\\ ny/z\\ unknown\\ 1\end{array}\right|$$