[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators
Contents
- Introduction
- Relational Proxies
-
- Problem Definition
- Relation-Agnostic Representations and Information Gap
- Sufficient Learner
- Learning Relation-Agnostic and Relation-Aware Representations
- Experiments
- References
Introduction
- 作者提出对于 FGVC 问题,模型不仅需要 global/local view 特征,还需要 cross-view relational information,即 “the way the local parts of an object combine to form its global view” 并给出了相应的理论框架。基于理论分析,作者进一步提出了 Relational Proxies 用于 FGVC
- Limitations. 作者获取 local views 的方法还可以进一步改进
Relational Proxies
- Notation. 给定 image x ∈ X \mathbf x ∈ \mathbb X x∈X with a label y ∈ Y \mathbf y ∈ \mathbb Y y∈Y,则 g = c g ( x ) \mathbf g = c_g(\mathbf x) g=cg(x) and L = { l 1 , l 2 , . . . l k } = c l ( x ) \mathbb L = \{\mathbf l_1,\mathbf l_2, ... \mathbf l_k\} = c_l(\mathbf x) L={l1,l2,...lk}=cl(x) 分别为 x \mathbf x x 的 global 和 set of local views,其中 c g , c l c_g,c_l cg,cl 为 cropping functions. f f f 为 encoder,用于将 global / local views 映射到 latent space ( z g = f ( g ) \mathbf z_g=f(g) zg=f(g), Z L = { f ( l ) : l ∈ L } = { z l 1 , z l 2 , . . . , z l k } \mathbb Z_{\mathbb L}=\{f(\mathbf l):\mathbf l\in\mathbb L\}=\{\mathbf z_{l_1},\mathbf z_{l_2},...,\mathbf z_{\mathbf l_k}\} ZL={f(l):l∈L}={zl1,zl2,...,zlk}). r \mathbf r r 为 global ( g \mathbf g g) 和 set of local ( L \mathbb L L) views 之间的关联信息 (i.e., cross-view relational information),它代表 “the way the local parts of an object combine to form its global view”
Problem Definition
- 作者首先给出了 k-distinguishability 的定义,并借此进一步定义了 FGVC 问题,即 FGVC 问题中必然存在两个类别,模型想要区分它们必须输入至少 k k k 个 local features


Relation-Agnostic Representations and Information Gap
- 现有的 FGVC 方法都只单独考虑了 global view 和 local views 而没有考虑 cross-view relational information,由此学得的 encoder 的特征空间即为 relation-agnostic representations

- 接下来,作者证明了 Proposition 1,即 relation-agnostic encoders 无法完全捕捉图像中编码的标签信息 (i.e., I ( x ; y ) > I ( z ; y ) I(\mathbf x;\mathbf y)>I(\mathbf z;\mathbf y) I(x;y)>I(z;y)),无法捕捉的信息量即为 Information Gap (i.e., I ( x ; y ) − I ( z ; y ) I(\mathbf x;\mathbf y)-I(\mathbf z;\mathbf y) I(x;y)−I(z;y)),并且 Information Gap 为 I ( x ; r ∣ z ) I(\mathbf x;\mathbf r|\mathbf z) I(x;r∣z)
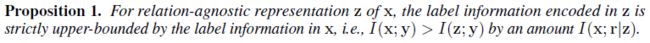
Proof.
- Chain rule for mutual information. (1) 由于 I ( x ; y ) + I ( x ; z ∣ y ) = I ( x ; z ) + I ( x ; y ∣ z ) I(\mathbf x; \mathbf y) + I(\mathbf x; \mathbf z|\mathbf y) =I(\mathbf x; \mathbf z) + I(\mathbf x; \mathbf y|\mathbf z) I(x;y)+I(x;z∣y)=I(x;z)+I(x;y∣z),并且 I ( x ; z ∣ y ) = 0 I(\mathbf x; \mathbf z|\mathbf y)=0 I(x;z∣y)=0 (since z \mathbf z z does not encode any more information about x \mathbf x x than y \mathbf y y),有
I ( x ; y ) = I ( x ; z ) + I ( x ; y ∣ z ) I(\mathbf x; \mathbf y) =I(\mathbf x; \mathbf z) + I(\mathbf x; \mathbf y|\mathbf z) I(x;y)=I(x;z)+I(x;y∣z)(2) 由于 I ( y ; z ) + I ( x ; z ∣ y ) = I ( x ; z ) + I ( y ; z ∣ x ) I(\mathbf y; \mathbf z) + I(\mathbf x; \mathbf z|\mathbf y) =I(\mathbf x; \mathbf z) + I(\mathbf y; \mathbf z|\mathbf x) I(y;z)+I(x;z∣y)=I(x;z)+I(y;z∣x),并且 I ( x ; z ∣ y ) = 0 I(\mathbf x; \mathbf z|\mathbf y)=0 I(x;z∣y)=0,有
I ( y ; z ) = I ( x ; z ) + I ( y ; z ∣ x ) I(\mathbf y; \mathbf z)=I(\mathbf x; \mathbf z) + I(\mathbf y; \mathbf z|\mathbf x) I(y;z)=I(x;z)+I(y;z∣x)(3) 由于 I ( x ; z ) + I ( y ; z ∣ x ) = I ( y ; z ) + I ( x ; z ∣ y ) I(\mathbf x; \mathbf z) + I(\mathbf y; \mathbf z|\mathbf x) =I(\mathbf y; \mathbf z) + I(\mathbf x; \mathbf z|\mathbf y) I(x;z)+I(y;z∣x)=I(y;z)+I(x;z∣y),并且 I ( y ; z ∣ x ) = 0 I(\mathbf y; \mathbf z|\mathbf x)=0 I(y;z∣x)=0 (since z \mathbf z z cannot encode any more information about y \mathbf y y than x \mathbf x x),有
I ( x ; z ) = I ( y ; z ) + I ( x ; z ∣ y ) I(\mathbf x; \mathbf z)=I(\mathbf y; \mathbf z) + I(\mathbf x; \mathbf z|\mathbf y) I(x;z)=I(y;z)+I(x;z∣y)(4) 由于 I ( x ; z ) + I ( r ; z ∣ x ) = I ( r ; z ) + I ( x ; z ∣ r ) I(\mathbf x; \mathbf z) + I(\mathbf r; \mathbf z|\mathbf x) =I(\mathbf r; \mathbf z) + I(\mathbf x; \mathbf z|\mathbf r) I(x;z)+I(r;z∣x)=I(r;z)+I(x;z∣r),并且 I ( r ; z ∣ x ) = 0 I(\mathbf r; \mathbf z|\mathbf x)=0 I(r;z∣x)=0 (since z \mathbf z z is relation-agnostic),有
I ( x ; z ) = I ( r ; z ) + I ( x ; z ∣ r ) I(\mathbf x; \mathbf z) =I(\mathbf r; \mathbf z) + I(\mathbf x; \mathbf z|\mathbf r) I(x;z)=I(r;z)+I(x;z∣r)(5) 由于 I ( x ; r ) + I ( r ; z ∣ x ) = I ( r ; z ) + I ( x ; r ∣ z ) I(\mathbf x; \mathbf r) + I(\mathbf r; \mathbf z|\mathbf x) =I(\mathbf r; \mathbf z) + I(\mathbf x; \mathbf r|\mathbf z) I(x;r)+I(r;z∣x)=I(r;z)+I(x;r∣z),并且 I ( r ; z ∣ x ) = 0 I(\mathbf r; \mathbf z|\mathbf x)=0 I(r;z∣x)=0,有
I ( x ; r ) = I ( r ; z ) + I ( x ; r ∣ z ) I(\mathbf x; \mathbf r) =I(\mathbf r; \mathbf z) + I(\mathbf x; \mathbf r|\mathbf z) I(x;r)=I(r;z)+I(x;r∣z) - Lemma 1.
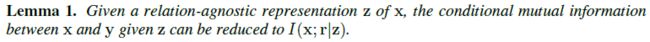 Proof. I ( x ; y ∣ z ) I(\mathbf x; \mathbf y|\mathbf z) I(x;y∣z) 表示 x \mathbf x x 用于预测 y \mathbf y y 的信息中 z \mathbf z z 无法捕捉的那一部分信息,作者认为这部分信息即为 I ( x ; r ) I(\mathbf x;\mathbf r) I(x;r) (i.e., the predictive information that r \mathbf r r does capture from x \mathbf x x) (这个等式基于作者的猜想,即 FGVC 需要 global view + local view + cross-view relationship),进一步将其用 chain rule 展开可得
Proof. I ( x ; y ∣ z ) I(\mathbf x; \mathbf y|\mathbf z) I(x;y∣z) 表示 x \mathbf x x 用于预测 y \mathbf y y 的信息中 z \mathbf z z 无法捕捉的那一部分信息,作者认为这部分信息即为 I ( x ; r ) I(\mathbf x;\mathbf r) I(x;r) (i.e., the predictive information that r \mathbf r r does capture from x \mathbf x x) (这个等式基于作者的猜想,即 FGVC 需要 global view + local view + cross-view relationship),进一步将其用 chain rule 展开可得
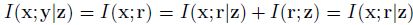
- Lemma 2.
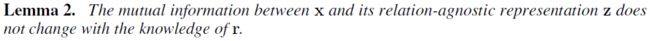 Proof.
Proof.
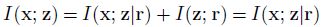
- Proposition 1.
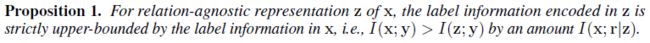 Proof. 首先将 I ( x , y ) I(\mathbf x,\mathbf y) I(x,y) 利用 chain rule 展开,然后代入 Lemma 1&2 的结果可得
Proof. 首先将 I ( x , y ) I(\mathbf x,\mathbf y) I(x,y) 利用 chain rule 展开,然后代入 Lemma 1&2 的结果可得
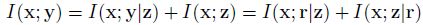 此外,由 chain rule I ( y ; z ) = I ( x ; z ) + I ( y ; z ∣ x ) I(\mathbf y; \mathbf z)=I(\mathbf x; \mathbf z) + I(\mathbf y; \mathbf z|\mathbf x) I(y;z)=I(x;z)+I(y;z∣x) 以及 I ( y ; z ∣ x ) = 0 I(\mathbf y; \mathbf z|\mathbf x)=0 I(y;z∣x)=0 可知, I ( y ; z ) = I ( x ; z ) I(\mathbf y; \mathbf z)=I(\mathbf x; \mathbf z) I(y;z)=I(x;z),代入上式可知
此外,由 chain rule I ( y ; z ) = I ( x ; z ) + I ( y ; z ∣ x ) I(\mathbf y; \mathbf z)=I(\mathbf x; \mathbf z) + I(\mathbf y; \mathbf z|\mathbf x) I(y;z)=I(x;z)+I(y;z∣x) 以及 I ( y ; z ∣ x ) = 0 I(\mathbf y; \mathbf z|\mathbf x)=0 I(y;z∣x)=0 可知, I ( y ; z ) = I ( x ; z ) I(\mathbf y; \mathbf z)=I(\mathbf x; \mathbf z) I(y;z)=I(x;z),代入上式可知
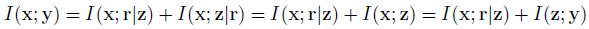
Sufficient Learner
- 作者首先定义了 Relation-Agnostic Representations 的几何性质,即 global view 特征远离 local view 特征,并且它们之间的距离正比于 Information Gap I ( x ; r ∣ z ) I(\mathbf x;\mathbf r|\mathbf z) I(x;r∣z) (个人理解:不存在 Information Gap 时,global view 和某个 local view 特征重合,说明该 local view 就是最重要的局部特征,relation 信息不再重要)

![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第1张图片](http://img.e-com-net.com/image/info8/bb65febb64c347dea7443975fc60dedb.jpg)
- 然后作者在 Lemma 3 中说明了,如果 encoder f f f 的下游目标是 cross-entropic,那么 f f f 会自然地生成 relation-agnostic representations,满足定义 4 中的几何性质

 Proof. 对于 FGVC 问题, f f f 的下游目标是 cross-entropic. 假如 f f f 生成的特征不是 relation-agnostic,则根据定义 4,global view z g \mathbf z_g zg 必在一个 local view z l \mathbf z_l zl 的邻域上,则 classifier 得到的信息就只有 { z g } ∪ Z L \ z l \{\mathbf z_g\}\cup\mathbb Z_L\backslash\mathbf z_l {zg}∪ZL\zl 而不是 { z g } ∪ Z L \{\mathbf z_g\}\cup\mathbb Z_L {zg}∪ZL. 而 FGVC 具有 k k k-distinguishability 性质,缺少一个 local view 信息会导致 classifier 误分类,这与 Axiom 1 相违背,因此 f f f 只会学得 relation-agnostic representations
Proof. 对于 FGVC 问题, f f f 的下游目标是 cross-entropic. 假如 f f f 生成的特征不是 relation-agnostic,则根据定义 4,global view z g \mathbf z_g zg 必在一个 local view z l \mathbf z_l zl 的邻域上,则 classifier 得到的信息就只有 { z g } ∪ Z L \ z l \{\mathbf z_g\}\cup\mathbb Z_L\backslash\mathbf z_l {zg}∪ZL\zl 而不是 { z g } ∪ Z L \{\mathbf z_g\}\cup\mathbb Z_L {zg}∪ZL. 而 FGVC 具有 k k k-distinguishability 性质,缺少一个 local view 信息会导致 classifier 误分类,这与 Axiom 1 相违背,因此 f f f 只会学得 relation-agnostic representations - 作者接着说明了用于学习 relation-agnostic representations z \mathbf z z 的 encoder f f f 不能用于建模 relationship r \mathbf r r (假设 local view 和 global view 是分别通过 encoder 得到相应特征的),因此 learner 必须使用单独的子模块用于建模 relationship r \mathbf r r
 Proof. 如果 f f f 要建模 cross-view relationships,它就需要不管输入是 global view 还是 local view 都输出相同的 r \mathbf r r,但根据 Lemma 3,global view 和 local view 的特征各不相同,因此 f f f 无法建模 relationship
Proof. 如果 f f f 要建模 cross-view relationships,它就需要不管输入是 global view 还是 local view 都输出相同的 r \mathbf r r,但根据 Lemma 3,global view 和 local view 的特征各不相同,因此 f f f 无法建模 relationship
Learning Relation-Agnostic and Relation-Aware Representations
- 根据上述描述,为了捕捉完整的标签信息 I ( x ; y ) I(\mathbf x;\mathbf y) I(x;y),模型需要同时考虑 (1) the relation-agnostic information z \mathbf z z (2) the cross-view relational information r \mathbf r r,模型主要分为两部分:(1) relation-agnostic agnostic encoder f f f;(2) cross-view relational function ξ ξ ξ
- Relation-Agnostic Representations. 作者首先通过 thresholding the final layer activations of a CNN encoder f f f and detecting the largest connected component in the thresholded feature map 来获取感兴趣区域,得到 global view g \mathbf g g 和 local views { l 1 , l 2 , . . . , l k } \{\mathbf l_1,\mathbf l_2,...,\mathbf l_k\} {l1,l2,...,lk} (i.e., sub-crops of g \mathbf g g) (For initial training stability, we consider five disjoint locations (four corners and the centre) of g \mathbf g g to be the set of local views. As training progresses, we also allow the model to learn from an increased number views obtained via random cropping. In the same way at inference time, the local views constitute a combination of the five disjoint crops along with some random crops.),将 views 分别经过 CNN encoder f f f 编码得到 relation-agnostic representations z g , Z L \mathbf z_g,\mathbb Z_{\mathbb L} zg,ZL
- Relational Embeddings. 作者认为 relationship modelling function ξ : ( g , L ) → r \xi:(\mathbf g,\mathbb L)\rightarrow \mathbf r ξ:(g,L)→r 应该满足 (1) View-Unification: Maps the set of all views { g , L } \{\mathbf g,\mathbb L\} {g,L} of an image x \mathbf x x to a single output r \mathbf r r; (2) Permutation Invariance (robust to changes in pose and relative orientation of local object parts): Produces the same output irrespective of the order of the local views. 对于 Permutation Invariance,作者采用 Attribute Summarization Transformer (AST),输入为 Z L ′ = [ z L , z l 1 , . . . , z l k ] \mathbf Z'_{\mathbb L}=[\mathbf z_{\mathbb L},\mathbf z_{l_1},...,\mathbf z_{l_k}] ZL′=[zL,zl1,...,zlk] (不加 position embed),其中 z L \mathbf z_{\mathbb L} zL 为新增的 summary embedding,模型结构采用多干个 Transformer 层, z L \mathbf z_{\mathbb L} zL 的输出即为归纳后的 local feature;对于 View-Unification,作者采用 MLP ρ : ( z g , z L ) → r \rho:(\mathbf z_g,\mathbf z_{\mathbb L})\rightarrow\mathbf r ρ:(zg,zL)→r
- Motivation: one can view the local-to-global relationship modelling function as an enumerative search algorithm - given a set of local views, it first enumerates all possible ways in which they can combine to form a meaningful global view (i.e., AST). Given that enumeration, it then finds the target solution by learning to identify the correct combination that matches with the global-view representation (i.e., ρ \rho ρ). Thus, the enumerate operation needs to be permutation invariant, as it has to consider all possible combinations of the inputs, and the find operation needs to be a view-unifier by construction. Behind our specific design choice was the motivation to keep the enumerate and find steps separate. This allows the model to have dedicated representation spaces for the two distinct subtasks, which in turn facilitates better convergence. Our AST thus produces the candidate enumerations of local-view aggregations, and the view-unification MLP ( ρ \rho ρ) finds the correct aggregation that matches with the global view.
- Learning Relational Proxies. 对于 FGVC,global/local view 和 cross-view relationships 都是区分类别的重要信息,因此作者将 global ( z g \mathbf z_g zg), summary of local ( z L \mathbf z_{\mathbb L} zL) 和 relational ( r \mathbf r r) 都当作 learnable metric space embedding,设置 c c c 个 proxies,采用 proxy-anchor loss 进行 metric learning
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第3张图片](http://img.e-com-net.com/image/info8/fa42b4811afc48f483913bfe24a32f15.jpg) 其中, ω = { z g , z L , r } \omega=\{\mathbf z_g,\mathbf z_{\mathbb L},\mathbf r\} ω={zg,zL,r}, Ω \Omega Ω 为 mini-batch 中 p \mathbf p p 的正样本集合, Ω ˉ \bar\Omega Ωˉ 为负样本集合, s s s 为余弦相似度
其中, ω = { z g , z L , r } \omega=\{\mathbf z_g,\mathbf z_{\mathbb L},\mathbf r\} ω={zg,zL,r}, Ω \Omega Ω 为 mini-batch 中 p \mathbf p p 的正样本集合, Ω ˉ \bar\Omega Ωˉ 为负样本集合, s s s 为余弦相似度
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第4张图片](http://img.e-com-net.com/image/info8/ce22d4cb69c141538ea55636ac78be91.jpg)
- Inference.

Experiments
- Comparison with State of the Art. 作者采用 ResNet50 pretrained on ImageNet 作为 backbone of relation-agnostic encoder f f f
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第6张图片](http://img.e-com-net.com/image/info8/e345ab11943b45a7a9b41e4d6f09e187.jpg)
- Ablation Studies
(1) Key components of the sufficient learner. Row 1 模型为 relation-agnostic encoder + a simple classification head;Row 2 模型将 RelationNet (i.e., view-unification MLP ρ \rho ρ) 替换为了固定的 relationship function,即 local 和 global representations 之间的距离,然后最小化同一类别不同样本的 relational distance value 之间的 Huber loss;Row 3 模型对 relational vectors 计算 pairwise contrastive loss;Rows 4 - 7 模型则是将 pair-based loss 改为 proxy based loss,其中没有采用 AST/RelationNet 的模型是将其替换为了线性层,输入为所有输入向量进行连接
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第7张图片](http://img.e-com-net.com/image/info8/73dc7113246743628f22a1d79f5269c3.jpg) (2) Conditioning of the relational proxies. relational proxies 由 summary of the local attributes z L \mathbf z_{\mathbb L} zL, the representation of the
(2) Conditioning of the relational proxies. relational proxies 由 summary of the local attributes z L \mathbf z_{\mathbb L} zL, the representation of the
global view z g \mathbf z_g zg, 以及 the relational vector r \mathbf r r 三部分组成,作者分别对这三部分进行了消融实验
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第8张图片](http://img.e-com-net.com/image/info8/7233d3b916cd479190875d9da1119cc4.jpg) (3) Results on ImageNet subsets
(3) Results on ImageNet subsets
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第9张图片](http://img.e-com-net.com/image/info8/d1ea4daac63b4b4789a99d15f722e0bb.jpg) (4) The optimal value of k k k for the k k k-distinguishability criterion. 对于 P FGVC \mathcal P_{\text{FGVC}} PFGVC,模型性能受提供给模型的 local views 数量 ∣ L ∣ |\mathbb L| ∣L∣ 影响,当 ∣ L ∣ |\mathbb L| ∣L∣ 少于 FGVC 所要求的最小值 k k k 时,模型的分类性能就会迅速下降。作者固定 local-crop size,在 3 个数据集下用实验验证了 the idea of k k k-distinguishability. 当 ∣ L ∣ |\mathbb L| ∣L∣ 到达 k = 7 / 8 k=7/8 k=7/8 时,模型性能达到最大值,而当 ∣ L ∣ |\mathbb L| ∣L∣ 继续增大时,新增信息为多为冗余或无关信息,模型性能没有明显提升
(4) The optimal value of k k k for the k k k-distinguishability criterion. 对于 P FGVC \mathcal P_{\text{FGVC}} PFGVC,模型性能受提供给模型的 local views 数量 ∣ L ∣ |\mathbb L| ∣L∣ 影响,当 ∣ L ∣ |\mathbb L| ∣L∣ 少于 FGVC 所要求的最小值 k k k 时,模型的分类性能就会迅速下降。作者固定 local-crop size,在 3 个数据集下用实验验证了 the idea of k k k-distinguishability. 当 ∣ L ∣ |\mathbb L| ∣L∣ 到达 k = 7 / 8 k=7/8 k=7/8 时,模型性能达到最大值,而当 ∣ L ∣ |\mathbb L| ∣L∣ 继续增大时,新增信息为多为冗余或无关信息,模型性能没有明显提升
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第10张图片](http://img.e-com-net.com/image/info8/3f36f176ca914e8f9d0f5c04e44fe729.jpg) (5) Correlation between ∣ L ∣ |\mathbb L| ∣L∣ and local patch size. 作者探索了 local view 数量以及大小对模型性能的影响,下表中 N / t N/t N/t 为 local view 的边长, N N N 为图像边长,表内数值代表相对 reported accuracy for FGVC Aircraft (95.25%) 的性能变化。
(5) Correlation between ∣ L ∣ |\mathbb L| ∣L∣ and local patch size. 作者探索了 local view 数量以及大小对模型性能的影响,下表中 N / t N/t N/t 为 local view 的边长, N N N 为图像边长,表内数值代表相对 reported accuracy for FGVC Aircraft (95.25%) 的性能变化。
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第11张图片](http://img.e-com-net.com/image/info8/717a36dd99d241adb2780f4c01040662.png) (6) Permutation invariance of AST
(6) Permutation invariance of AST
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第12张图片](http://img.e-com-net.com/image/info8/3e296b2134054dcdbec0f048e1f2800a.jpg)
- Visual Representations of Cross-View Local Relationships. 作者选取图像中的部分 local views,对 Cross-View Local Relationships 进行了可视化,node 代表 local view,边的粗细对应 AST 最后一层中 local views 之间的 mutual attention score,只有 attention score 超过均值的边才会被画出。可以看到,视觉上相似的图像可以通过 local views 之间的关系进行区分 (When two categories share a large number of local attributes, this cross-view relational information becomes the only discriminator.),同时作者也指出存在利用 local views 之间的关系也无法区分的图像
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第13张图片](http://img.e-com-net.com/image/info8/09b2e56d96514fd388b6116fda48d4b0.jpg)
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第14张图片](http://img.e-com-net.com/image/info8/e3c927a11ff040f09366d3af9672833d.jpg)
- Cross-view relationships for intra-class variations. FGVC 通常会面临很大的类间差异性,而考虑 fine-grained geometric relationships 有助于缓解这一问题
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第15张图片](http://img.e-com-net.com/image/info8/0462edf5b8864084b9eda61bd3a78c2e.jpg)
- Importance of Relational Information
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第16张图片](http://img.e-com-net.com/image/info8/81ceadcfe41a41d481a79f6b2be3c9be.jpg)
- Relation-Agnosticity of Relational Proxies. 作者用实验验证了 Lemma 3, i.e., f f f will produce relation-agnostic representations if the downstream objective is cross-entropic in nature. 注意到有一些 glocal embed 位置和 local embed 重合,这是因为那些图片的 local views 已经提供了足够多的信息,global view 的信息就变得冗余了,因此 global view 就和 local view 合并到了一起 (并不违反 k k k-distinguishability)
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第17张图片](http://img.e-com-net.com/image/info8/2a591fb61ab1430784d2afbe8461cf0e.jpg)
References
- Chaudhuri, Abhra, et al. “Relational Proxies: Emergent Relationships as Fine-Grained Discriminators.” (NeurIPS 2022).
- code: https://github.com/abhrac/relational-proxies
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第2张图片](http://img.e-com-net.com/image/info8/4d91f1337265436087651a0b480bcf9f.jpg)
![[NeurIPS 2022] Relational Proxies: Emergent Relationships as Fine-Grained Discriminators_第5张图片](http://img.e-com-net.com/image/info8/876939fddde945e2855270d7321dfa8b.jpg)