深度学习-实验1

一、Pytorch基本操作考察（平台课+专业课）

1. 使用初始化一个 ×的矩阵 和一个 ×的矩阵 ，对两矩阵进行减法操作（要求实现三种不同的形式），给出结果并分析三种方式的不同（如果出现报错，分析报错的原因）同时需要指出在 计算过程中发生了什么

import torch
a = torch.rand(1,3)
b = torch.rand(2,1)
print('a=',a)
print('b=',b)

print(a-b)

print(torch.sub(a,b))

a.sub_(b)

2. 利用 创建两个大小分别 × 和 ×的 随机数矩阵 和 ，要求服从均值为 0 ，标准差 0.01 为的 正态分布 ；② 对第二步得到的矩阵 进行形状变换得到 的转置 ；③ 对上述得到的矩阵 和矩阵 求矩阵相乘

import torch
import numpy as np
x = np.random.normal(0,0.01,3*2)
y = np.random.normal(0,0.01,4*2)
P = torch.from_numpy(x).clone().view(3,2)
print("P矩阵为:",P)
Q = torch.from_numpy(y).clone().view(4,2)
print("Q矩阵为:",Q)
Qt = Q.t()
print("Qt矩阵为:",Qt)
R = torch.mm(P,Qt)
print("P矩阵与Qt矩阵相乘的结果为:",R)

3. 给定公式3=1+2=2+3 且 =1。利用学习所得到的 Tensor 的相关知识，求 3对 的梯度，即 3。要求在计算过程中，在计算 3 时中断梯度的追踪， 观察结果并进行原因分析

import torch
x = torch.tensor(1.,requires_grad=True)
y1 = x**2
y2 = x**3
y3 = y1+y2
y3.backward()
print("计算x的梯度:",x.grad)

import torch
x = torch.tensor(1.,requires_grad=True)
y1 = x**2
with torch.no_grad():
  y2 = x**3
y3 = y1+y2
y3.backward()
print("不计算x三次方的梯度:",x.grad)

二、手动实现logistic回归

1. 要求动手从 0 实现 logistic 回归 （只借助 Tensor 和 Numpy 相关的库）在 人工构造的数据集上进行训练和测试，并从 loss 以及训练集上的准确率等多个角度对结果进行分析

导入包

import torch
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import torch.nn as nn

生成训练集

#标准化数据
def sdata(data):
  sdata = np.interp(data, (data.min(), data.max()), (0, 1))
  return sdata
num_examples = 500

num1 = np.c_[np.random.normal(3, 1, (num_examples , 2)),np.ones(num_examples)]
num2 = np.c_[np.random.normal(1, 1, (num_examples , 2)),np.zeros(num_examples)]
num = np.vstack((num1,num2))
np.random.shuffle(num)#打乱数据
np.savetxt('test',(num))

#将数据等比例压缩在0-1之间
snum1 = sdata(num[:,0]).reshape(num_examples*2,1)
snum2 = sdata(num[:,1]).reshape(num_examples*2,1)
snum = np.concatenate((snum1,snum2,num[:,2].reshape(num_examples*2,1)), axis=1)

#将numpy格式的数据转为tensor格式
num1_tensor = torch.tensor((np.c_[snum[:,0],snum[:,1]]),dtype=torch.float)
num2_tensor = torch.tensor(snum[:,2],dtype=torch.float).unsqueeze(1)

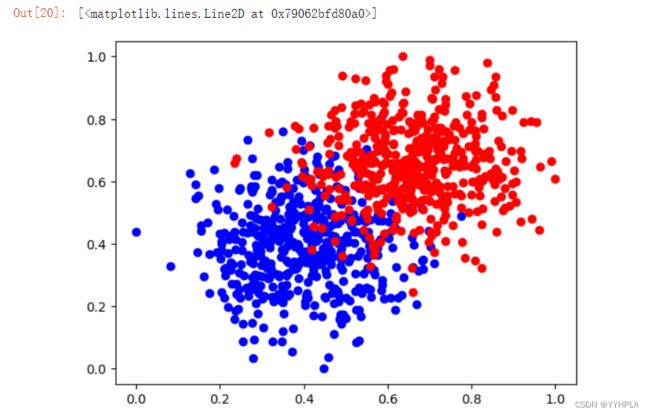
#绘制数据的图像
column_values = num[:,2]
xy0 = snum[column_values == 0]
xy1 = snum[column_values == 1]
plt.plot(xy0[:,0],xy0[:,1],'bo', label='x_1')
plt.plot(xy1[:,0],xy1[:,1],'ro', label='x_1')

运行结果：

损失函数：二元交叉熵

def binary_loss(y_pred, y):
  loss = nn.BCELoss()
  return loss(y_pred , y)

优化算法：梯度优化算法

def sgd(w,b):
  w.data = w.data - 0.1 * w.grad.data
  b.data = b.data - 0.1 * b.grad.data
  w.grad.zero_()
  b.grad.zero_()

构建模型和模型训练

#sigmoid函数
def sigmoid(x):
    return 1 / (1 + torch.exp(-x))

def logistic_regression(x):
  return sigmoid(torch.mm(x, w) + b)

#正确率计算
def accu(y_pred,y):
  correct = (y_pred == y).sum()/y.numel()
  return correct

w = torch.rand(2, 1, requires_grad=True)##torch.rand默认随机产生的数据都是0-1
b = torch.zeros(1, requires_grad=True)

#模型训练
for nums in range(1,1000):
  y_pred = logistic_regression(num1_tensor)
  loss = binary_loss(y_pred, num2_tensor)
  loss.backward()
  sgd(w,b)

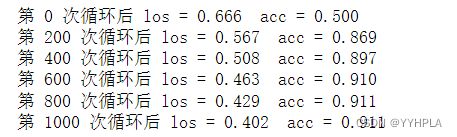
  if nums%200==0 :
    mask = y_pred.ge(0.5).float()
    acc = accu(mask,num2_tensor)
    print('第',nums,'次循环后','los =',f"{loss.data.float().item():.3f}",' acc =',f"{acc.item():.3f}")
print('第',nums+1,'次循环后','los =',f"{loss.data.float().item():.3f}",' acc =',f"{acc.item():.3f}")

运行结果：

绘制图像

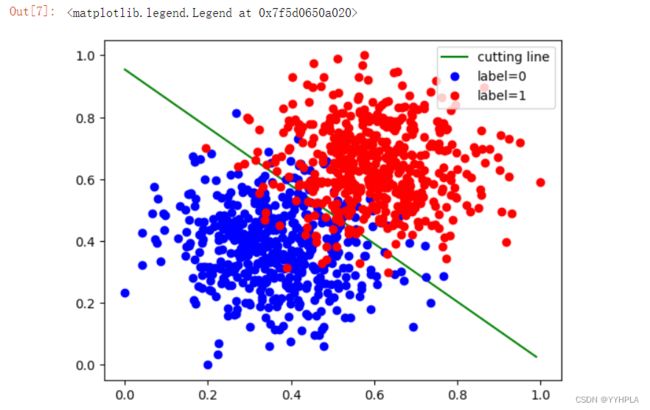
cline_x = np.arange(0, 1, 0.01)
cline_y = (-w[0].data[0] * cline_x - b.data[0]) / w[1].data[0]

column_values = num[:,2]
xy0 = snum[column_values == 0]
xy1 = snum[column_values == 1]

plt.plot(cline_x, cline_y, 'g', label='cutting line')
plt.plot(xy0[:,0],xy0[:,1],'bo', label='label=0')
plt.plot(xy1[:,0],xy1[:,1],'ro', label='label=1')
plt.legend(loc='best')

运行结果：

2. 利用torch.nn实现logistic回归在人工构造的数据集上进行训练和测试，并对结果进行分析并从loss以及训练集上的准确率等多个角度 对结果进行分析

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np

# 构造训练数据集
# 假设特征向量为2维，标签为0或1
def sdata(data):
  sdata = np.interp(data, (data.min(), data.max()), (0, 1))
  return sdata

num_examples = 500

num1 = np.c_[np.random.normal(3, 1, (num_examples , 2)),np.ones(num_examples)]
num2 = np.c_[np.random.normal(1, 1, (num_examples , 2)),np.zeros(num_examples)]
num = np.vstack((num1,num2))
np.random.shuffle(num)#打乱数据
np.savetxt('test',(num))

#将数据等比例压缩在0-1之间
snum1 = sdata(num[:,0]).reshape(num_examples*2,1)
snum2 = sdata(num[:,1]).reshape(num_examples*2,1)
snum = np.concatenate((snum1,snum2,num[:,2].reshape(num_examples*2,1)), axis=1)

#将numpy格式的数据转为tensor格式
train_features = torch.tensor((np.c_[snum[:,0],snum[:,1]]),dtype=torch.float)
train_labels = torch.tensor(snum[:,2],dtype=torch.float).unsqueeze(1)

# 定义 logistic 回归模型
class LogisticRegression(nn.Module):
    def __init__(self, input_dim):
        #继承
        super().__init__()
        self.linear = nn.Linear(input_dim, 1)#设置一个全连接层

    def forward(self, x):
        out = self.linear(x)#先经过一遍全连接层，得到out
        self.sigmoid = nn.Sigmoid()
        out = self.sigmoid(out)#使用out经过激活函数
        return out


# 初始化模型和损失函数
net = LogisticRegression(2)
BCEloss = nn.BCELoss()#损失函数
optimizer = optim.SGD(net.parameters(), lr=0.01)##优化器

# 迭代训练
num_epochs = 6000
for epoch in range(num_epochs):
    # 前向传播
    outputs = net(train_features)
    #算下loss
    loss = BCEloss(outputs.flatten(), train_labels.float().squeeze())

    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()#参数更新

# 打印最终的损失
print(f"Final loss: {loss.item()}")

# 在训练集上进行预测
with torch.no_grad():
  predicted_labels = net(train_features).round()

# 计算训练集上的准确率
accuracy = (predicted_labels == train_labels).sum().item() / len(train_labels)
print(f"Accuracy on the training set: {accuracy}")

运行结果：

动手实现softmax回归

1. 要求动手从 0 实现 softmax 回归 （只借助 Tensor 和 Numpy 相关的库）在 Fashion MNIST 数据集上进行训练和测试 ，并从 loss 、训练集以及测试集上的准确率等多个角度对结果进行分析

导入数据

# 1、加载Fashion-MNIST数据集（采用已划分好的训练集和测试集）
#训练集
mnist_train = torchvision.datasets.FashionMNIST(
    root='~/Datasets/FashionMNIST',
    train=True,
    download=True,
    transform=transforms.ToTensor())
#测试集
mnist_test = torchvision.datasets.FashionMNIST(
    root='~/Datasets/FashionMNIST',
    train=False,
    download=True,
    transform=transforms.ToTensor()
)

数据加载

BATCH_SIZE = 500
train_loader = torch.utils.data.DataLoader(
    dataset = mnist_train,
    batch_size=BATCH_SIZE,
    shuffle=True,
    num_workers=0
)

test_loader = torch.utils.data.DataLoader(
    dataset = mnist_test,
    batch_size=BATCH_SIZE,
    shuffle=False,
    num_workers=0
)

损失函数：交叉熵损失函数（代码略）

优化算法：SGD（代码略）

搭建softmax回归模型

def softmax(X):
  X_exp = torch.exp(X)
  partition = X_exp.sum(1, keepdim=True)
  return X_exp / partition


def net(X):
  return softmax(torch.mm(X.view((-1, 784)), W) + b)

准确率计算

def evaluate_accurcy(data_iter): #测试集正确率计算
    right_count, all_num = 0.0, 0
    for x, y in data_iter:
        right_count += (net(x).argmax(dim=1) == y).float().sum().item()
        all_num += y.shape[0]
    return right_count / all_num


def corrcet_num(predicted_probs, labels):

    predicted_labels = torch.argmax(predicted_probs, dim=1)

    correct = (predicted_labels == labels).sum().item()

    return correct

模型训练

lr = 0.1
num_epochs = 5
W = torch.normal(0, 0.1, (784, 10), dtype=torch.float32).requires_grad_()
b = torch.normal(0, 0.01, (1, 10), dtype=torch.float32).requires_grad_()

for epoch in range(num_epochs):
    train_right_sum, train_all_sum, train_loss_sum = 0.0, 0, 0.0
    for X, y in train_loader:
        y_pred = net(X)
        loss = CEloss(y_pred, y).sum()
        loss.backward()
        sgd([W, b], lr, BATCH_SIZE)
        train_loss_sum += loss.item()
        train_right_sum += corrcet_num(y_pred,y) #训练集正确数量
        train_all_sum += y.shape[0]
    test_acc = evaluate_accurcy(test_loader)  # 测试集正确率
    print('epoch:{}|loss:{}'.format(epoch, train_loss_sum/train_all_sum))
    print('训练集正确率:{}|测试集正确率:{}'.format(train_right_sum/train_all_sum, test_acc))

输出结果：

2. 利用 torch.nn 实现 softmax 回归在 Fashion MNIST 数据集上进行训练和测试，并从 loss ，训练集以及测试集上的准确率等多个角度对结果进行分析

import torch
import torch.nn as nn
from torch import tensor
import torch.optim as optim
import numpy as np
import torchvision
import torchvision.transforms as transforms

mnist_train = torchvision.datasets.FashionMNIST(
    root='~/Datasets/FashionMNIST',
    train=True,
    download=True,
    transform=transforms.ToTensor())  # 将所有数据转换为Tensor
mnist_test = torchvision.datasets.FashionMNIST(
    root='~/Datasets/FashionMNIST',
    train=False,
    download=True,
    transform=transforms.ToTensor()
)

BATCH_SIZE = 256
train_loader = torch.utils.data.DataLoader(
    dataset = mnist_train,
    batch_size=BATCH_SIZE,
    shuffle=True,
    num_workers=0
)

test_loader = torch.utils.data.DataLoader(
    dataset = mnist_test,
    batch_size=BATCH_SIZE,
    shuffle=False,
    num_workers=0
)

input_dim = 784
output_dim = 10



class SoftmaxRegression(nn.Module):
    def __init__(self, input_dim , output_dim):
        #继承
        super().__init__()
        self.linear = nn.Linear(input_dim, output_dim)#设置一个全连接层

    def forward(self, x):
        x = x.view(-1,input_dim)
        out = self.linear(x)#先经过一遍全连接层，得到out
        self.softmax = nn.Softmax()
        out = self.softmax(out)#使用out经过激活函数
        return out

net = SoftmaxRegression(input_dim,output_dim)
lr = 0.1
CEloss = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr)

num_epoch = 5

def evaluate_accurcy(data_iter): #测试集正确率计算
    right_count, all_num = 0.0, 0
    for x, y in data_iter:
        right_count += (net(x).argmax(dim=1) == y).float().sum().item()
        all_num += y.shape[0]
    return right_count / all_num

def corrcet_num(predicted_probs, labels):
    predicted_labels = torch.argmax(predicted_probs, dim=1)
    correct = (predicted_labels == labels).sum().item()
    return correct

for epoch in range(num_epoch):
    train_right_sum, train_all_sum, train_loss_sum = 0.0, 0, 0.0
    for X, y in train_loader:
      # 前向传播
      y_pred = net(X)
      #算下loss
      loss = CEloss(y_pred, y)

      # 反向传播和优化
      loss.backward()
      optimizer.step()
      optimizer.zero_grad()#参数更新

      train_loss_sum += loss.item()
      train_right_sum += corrcet_num(y_pred,y) #训练集正确数量
      train_all_sum += y.shape[0]
    test_acc = evaluate_accurcy(test_loader)


    print('epoch:{}|loss:{}'.format(epoch, train_loss_sum/train_all_sum))
    print('训练集正确率:{}|测试集正确率:{}'.format(train_right_sum/train_all_sum, test_acc))