卷积神经网络——中篇【深度学习】【PyTorch】

5、卷积神经网络

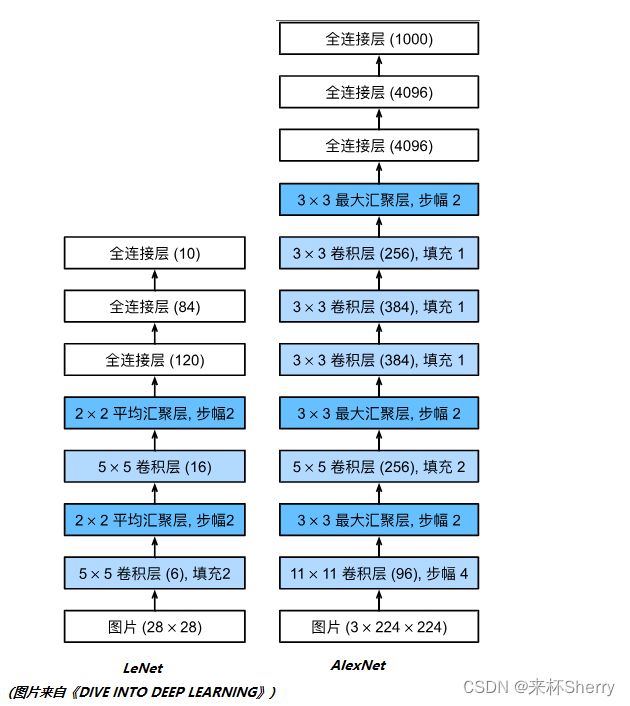
5.5、经典卷积神经网络（LeNet）

5.5.1、理论部分

早期神经网络，先使用卷积层学习图片空间信息，然后全连接层转换到类别空间。

5.5.2、代码实现

定义一个 Sequential块

和LeNet-5相比，这里去掉了最后一层的高斯激活。

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

检查输出形状

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

Conv2d output shape: 	 torch.Size([1, 6, 28, 28])
Sigmoid output shape: 	 torch.Size([1, 6, 28, 28])
AvgPool2d output shape: 	 torch.Size([1, 6, 14, 14])
Conv2d output shape: 	 torch.Size([1, 16, 10, 10])
Sigmoid output shape: 	 torch.Size([1, 16, 10, 10])
AvgPool2d output shape: 	 torch.Size([1, 16, 5, 5])
Flatten output shape: 	 torch.Size([1, 400])
Linear output shape: 	 torch.Size([1, 120])
Sigmoid output shape: 	 torch.Size([1, 120])
Linear output shape: 	 torch.Size([1, 84])
Sigmoid output shape: 	 torch.Size([1, 84])
Linear output shape: 	 torch.Size([1, 10])

模型训练

Fashion-MNIST数据集

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

训练&评估LeNet-5

lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.452, train acc 0.832, test acc 0.812
46735.1 examples/sec on cuda:0

5.6、深度卷积神经网络（AlexNet）

5.6.1、理论部分

相较于 LeNet 改进：

• 丢弃法（控制复杂度）；

• ReLu（减缓梯度消失）；

• MAxPooling；

• 数据增强；

• 架构（卷积窗口更大、通道更多、全连接层更大、更深）。

  

5.6.2、代码实现

定义Sequential块

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

读取数据集

batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

训练

lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

5.7、使用块的网络（VGG）

5.7.1、理论部分

VGG块

AlexNet 卷积层、汇聚层重复成块，实现更大更深的网络。

不同的卷积块个数和超参数可得到不同的VGG块。

相较于 AlexNet ：

5.7.2、代码实现

定义VGG块

import torch
from torch import nn
from d2l import torch as d2l


def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

实现VGG-11

VGG-11网络使用8个卷积层和3个全连接层。

定义超参数

#指定了每个VGG块里卷积层个数和输出通道数
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

构建一个高度和宽度为224的单通道数据样本X

X = torch.randn(size=(1, 1, 224, 224))

训练模型

ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

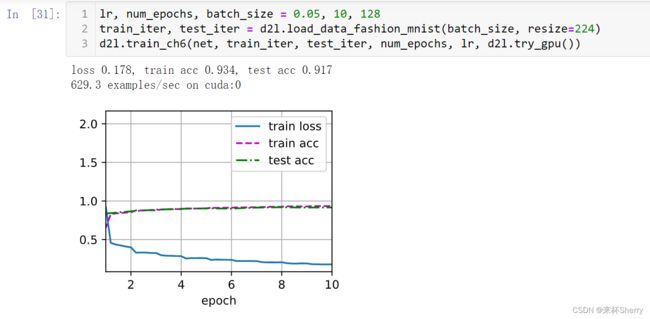
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

5.8、网络中的网络（NiN）

5.8.1、理论部分

为什么提出NiN？

全连接层是网络里参数比重最高的地方（参数=输入通道*高*宽*输出通道*高*宽），尤其是卷积后的第一个全连接层。而卷积层参数就小得多。所以用卷积层替代全连接层，参数会更少。

NiN架构

• 交替使用NiN块和MaxPool（stride=2），NiN块的两个1×1卷积层对每个像素增加了非线性；

• 逐步缩小高宽，增大通道数；

  输入通道数=类别数

• 全局AvgPool 得到输出，无全连接层，使用全局AvgPool代替全连接层，这样做不容易过拟合，需要的参数更少。

5.9、含并行连结的网络（GoogLeNet）

5.9.1、理论部分

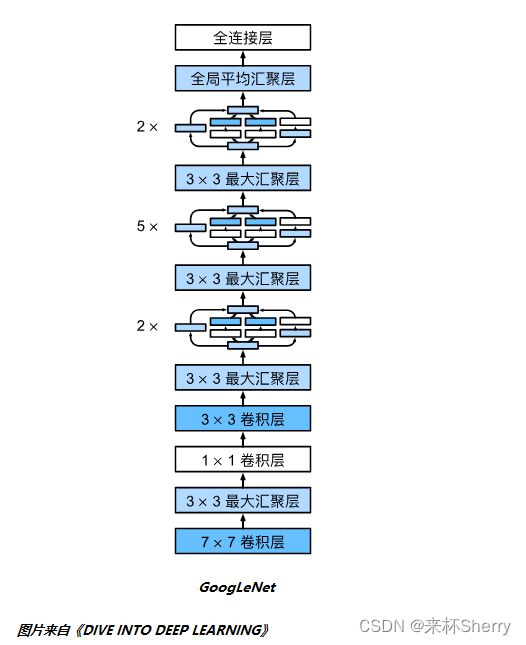
GoogLeNet架构

5段，9个inception块。

• 模型参数小，计算复杂度低；

• Inception块，从四个路径不同层面抽取信息，在输出通道维合并。

  

• 第一个百层网络，有后续改进。

卷积层后面一定要跟着池化层吗？

卷积层和池化层通常一起使用在卷积神经网络（CNN）中，这是因为它们在不同的层次上提供了一些有益的特性，帮助网络更好地捕获图像特征、减少过拟合以及降低计算负担。虽然不是一定要跟着池化层，但这种组合在很多情况下被证明是有效的。

经过卷积层之后，特征图包含了更高级的特征表示。池化操作有助于进一步提取这些抽象特征，从而让网络更加关注物体的重要特征，而不是像素级细节。

池化操作有助于减少模型对训练数据中微小变化的敏感性，从而降低过拟合的风险。通过降低特征图的维度，池化层可以在一定程度上提取出更稳定的特征，减少模型对噪声的响应。

池化层可以减小特征图的尺寸，通过保留主要信息的同时降低计算复杂度。池化操作还有助于增加模型对于平移、旋转和缩放等空间变化的鲁棒性，提供了一定程度的空间不变性。这对于图像识别任务很有帮助，因为我们希望模型能够识别出物体不受其在图像中的位置变化的影响。

池化层在减小特征图尺寸的同时，也减少了网络中的参数数量。这有助于减轻模型的计算负担和内存需求，特别是在深层网络中。

5.9.2、代码实现

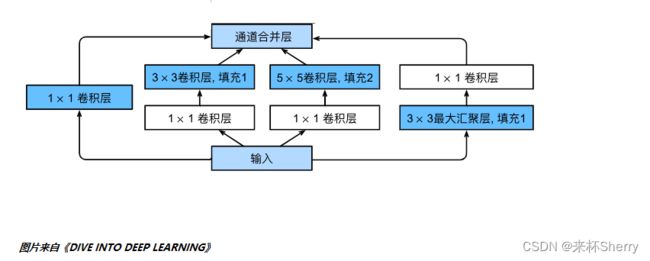
定义Inception块

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

将GoogLeNet定义成5个 Sequential块

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

#将输入的高和宽从224降到96，这简化了计算
X = torch.rand(size=(1, 1, 96, 96))
#可验证块形状（略）

训练模型

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

闲谈

个性化定制界面与极简版原装界面：我们为什么选择个性化？

随着科技的不断发展，人们对于界面设计和用户体验的要求也越来越高。在软件、应用程序、网站等各种数字平台中，界面是用户与系统之间的桥梁，直接影响着用户的使用感受。在这个背景下，个性化定制界面和极简版原装界面成为了用户选择的两种不同趋势。

---

个性化定制界面，作为一种用户体验的关键创新，强调了用户的个人喜好和需求。通过允许用户自定义颜色、布局、字体等元素，个性化界面能够更好地满足不同用户的审美和操作偏好。这种方式可以使用户感到更加亲近和熟悉，提升了用户的情感连接。此外，个性化界面还能够提升用户的工作效率和生产力，因为用户可以将界面调整为最适合自己工作方式的状态，减少不必要的操作和寻找时间。

---

然而，极简版原装界面也有其独特的优势。极简界面强调简洁、直观，去除了冗余的元素和复杂的设计，使用户能够更加专注地完成任务。这种设计风格适用于那些追求高效率、集中注意力的用户群体。极简界面的设计哲学是“少即是多”，它通过减少视觉噪音和干扰，使用户能够更轻松地掌握操作逻辑，降低了学习成本。

---

那么，为什么选择个性化界面？个性化界面在满足用户需求方面具有独特的优势。每个人的审美和操作习惯都不同，个性化界面可以让用户在熟悉和舒适的环境中工作，提升工作效率和用户满意度。同时，个性化界面还有助于品牌塑造和用户情感连接的建立，因为用户可以将界面个性化地定制成与品牌形象相符的样式。

---

综合来看，个性化定制界面和极简版原装界面各有其适用场景。在不同的用户需求和使用场景下，选择合适的界面设计风格能够更好地满足用户的期望。无论是追求与品牌形象一致的个性化，还是追求高效率和专注的极简体验，界面设计都应该以用户为中心，创造出更优秀的用户体验。