0x06多层感知机
感知机
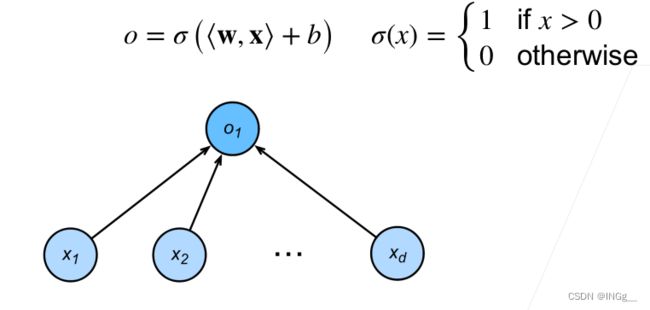
感知机形象的来看就是我们接触过的一个只有两个部分组成(输出和输入)组成的最简单的神经网络之一。
给定输入x,权重w和偏移b以及一个感知函数,感知机就能输出:
这个函数可以形象的用作二分类问题,o输出几就可以把他作为哪个类
但是单层感知机有一个很大的局限性就是——它只能解决线性可分的问题,也就是在超平面上只能构成一条线来区分数据
异或问题,也就是XOR问题就是非线性可分的问题,为了解决它,引出了多层感知机
多层感知机
使用多层感知机就可以在超平面上构造两条线将数据区分开了
我们使用多层感知机配合上softmax计算就能解决一些多分类的问题,这里把softmax也可以看做层一对一而非全连接的层,输出当前样本可能是哪一个类别的概率
在每个隐藏层中都会添加激活函数来对神经元做激活,常见的激活函数有SIGMOD、Relu
激活函数
激活函数都是非线性函数
SIGMOD函数能够将一个实数域的结果映射到(0,1)之间
s i g m o i d = 1 1 + e x p ( − x ) sigmoid=\frac{1}{1+exp(-x)} sigmoid=1+exp(−x)1
这个激活函数在以前比较常用,因为他会存在一些梯度丢失的问题导致现在也很少有人用了
目前比较常用的函数——Relu激活函数
他的数学表达很简单
R e L u ( x ) = m a x ( x , 0 ) ReLu(x)=max(x,0) ReLu(x)=max(x,0)
本质上是一个一段分段的非线性函数
代码实现
在本节书中的代码实现中,我们发现在每一个实现中为了实现一个多分类的多层个感知机,使用了softmax计算,但是实际上他并没有直接显式的使用softmax来计算每一个输出层神经元输出的值,而是在计CrossEntropyLoss中计算了softmax
# 构建模型
net = nn.Sequential(nn.Flatten(), # 该层的作用是将图片展开成一个一维的向量
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights); # 初始化参数
# 设定一些超参数
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none') # 表示直接返回n分样本的loss
trainer = torch.optim.SGD(net.parameters(), lr=lr) # 对参数使用SGD来优化
# 加载数据以及训练
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
# 这是那个训练函数,以免不知道内部是怎么用的
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save
"""训练模型(定义见第3章)"""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
def train_epoch_ch3(net, train_iter, loss, updater): #@save
"""训练模型一个迭代周期(定义见第3章)"""
# 将模型设置为训练模式
if isinstance(net, torch.nn.Module):
net.train()
# 训练损失总和、训练准确度总和、样本数
metric = Accumulator(3)
for X, y in train_iter:
# 计算梯度并更新参数
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# 使用PyTorch内置的优化器和损失函数
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# 使用定制的优化器和损失函数
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
# metric的第一个元素是所有小批量损失函数值的总和。最后,我们将它除以样本数metric[2]来得到训练集上的平均损失。因此,返回的metric[0] / metric[2]是训练损失。