深入浅出 栈和队列(附加循环队列、双端队列)
栈和队列
- 一、栈 概念与特性
- 二、Stack 集合类及模拟实现
-
- 1、Java集合中的 Stack
- 2、Stack 模拟实现
- 三、栈、虚拟机栈、栈帧有什么区别?
- 四、队列 概念与特性
- 五、Queue集合类及模拟实现
-
- 1、Queue的底层结构
-
- (1)顺序结构
- (2)链式结构
- 2、Java集合中的 Queue
- 3、Queue 模拟实现
- 六、设计循环队列
-
- 1、循环队列涉及的两个关键问题
-
- (1)问题 1 解决方案
- (2)问题 2 解决方案
- 2、循环队列具体实现
- 七、Deque 集合类
一、栈 概念与特性
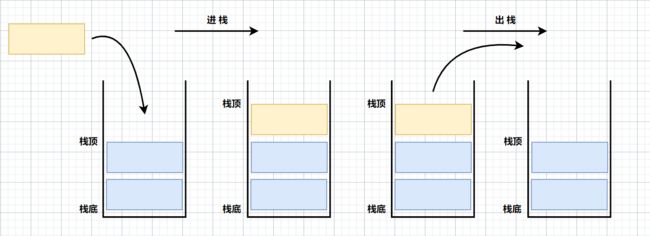
一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈
顶,另一端称为栈底。栈中的数据元素遵守后进先出 LIFO(Last In First Out)的原则。
二、Stack 集合类及模拟实现
1、Java集合中的 Stack
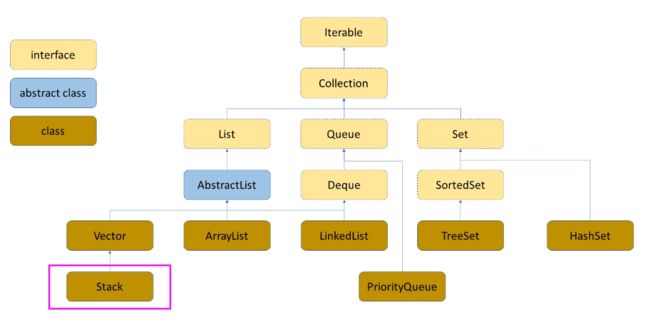
在Java集合中 Stack 集合类可以表示栈,Stack继承了Vector,Vector和ArrayList类似,都是动态的顺序表,因此Stack 底层维护的也是一个动态顺序表。
我们可以先看一下Stack中给出的常用方法:
构造方法
| 方法 | 解释 |
|---|---|
| Stack() | 构造一个空的栈 |
常用方法
| 方法 | 功能 |
|---|---|
| E push(E e) | 将元素 e 入栈,并返回 e |
| E pop() | 将栈顶元素出栈并返回 |
| E peek() | 获取栈顶元素 |
| int size() | 获取栈中有效元素个数 |
| boolean empty() | 检测栈是否为空 |
2、Stack 模拟实现
有了顺序表和链表的基础,栈的实现就非常的简单了,下面就直接给出顺序栈的实现代码,大家可以参照注释进行理解:
public class MyStack {
// 数组
public int[] elem;
// 栈顶
public int top;
// 构造方法(初始化顺序栈)
public MyStack() {
elem = new int[5];
}
//1.压栈:E push(E e)
//检测容量
private boolean isFull() {
return top == elem.length;
}
public int push(int e) {
if (isFull()) {
// 如果栈满就扩容
elem = Arrays.copyOf(elem,2*elem.length);
}
elem[top++]=e;
return e;
}
//2.出栈:E pop()
public int pop() {
// 如果栈空,抛异常(这里可以自定义实现一个异常类)
if (empty()) {
throw new EmptyException("空栈!");
}
// 正常出栈
return elem[--top];
}
//3.获取栈顶元素:E peek()
public int peek() {
return elem[top-1];
}
//4.获取栈中有效元素个数:int size()
public int size() {
return top;
}
//5.检测栈是否为空:boolean empty()
public boolean empty() {
return top == 0;
}
}
上面实现的 栈 底层是一个动态数组,它的入栈和出栈都达到了O(1)。其实栈的底层也可以实现成链表的结构:
(1) 底层为单向链表。 如果底层维护一个单链表,那么可以将入栈实现为头插;出栈实现为头删;这样以来它的时间复杂的也可以达到O(1)。
(2)底层为双向链表。 对于双向链表来说,由于同时记录了head结点和last结点,并且每个结点的前后结点都是明确的,故无论是在头部使用插入删除模拟入栈出栈,还是在尾部实现,复杂度都可以达到O(1)。
这一点在Java集合类LinkedList中给出的接口方法中,得到了体现,它里面就提供了push()、pop()、peek()等方法。
三、栈、虚拟机栈、栈帧有什么区别?
- 栈是一种数据结构,用于存储和管理数据。
- 虚拟机栈是
JVM在执行Java程序时使用的一块内存区域,包含了线程的栈帧。- 栈帧是虚拟机栈中的一个元素,用于存储方法调用的信息。
四、队列 概念与特性
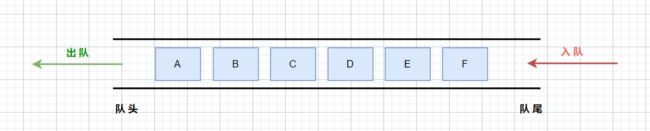
只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 的特点。
进行插入操作的一端称为队尾(Tail/Rear),进行删除操作的一端称为队头(Head/Front)
五、Queue集合类及模拟实现
1、Queue的底层结构
众所周知,无论是栈也好,队列也好,它们的本质都是一个容器,既然是容器那么底层就有两种结构:顺序结构、链式结构。那么队列的底层究竟是用 顺序结构还是链式结构?如果使用链式结构,那么是使用单向还是双向呢?下面我们一起来探讨一下:
(1)顺序结构
我们知道,队列的两个关键操作是,入队和出队。如果使用顺序结构,那么意味着它的底层将维护一个数组,此时我们有两种实现方案:
- 方案一: 使用数组的头插完成入队,使用数组的尾删实现出队
- 方案二: 使用数组的尾插完成入队,使用数组的头删实现出队
方案一分析:使用方案1,入队的话使用头插法,需要挪动数组元素,复杂度为O(N);出队的复杂度可以达到O(1)。
方案二分析:使用方案2,入队复杂度可达到O(1),而出队,由于使用的头删,每次需要移动大量的元素,复杂度达到了O(N)。所以这两种方案均不能保证入队和出队的复杂度达到O(1),因此不建议采用。但是可通过循环数组,解决上述问题(后面讲解)
(2)链式结构
- 方案一:使用单向链表。
- 方案二:使用双向链表。
方案一分析:如果采用方案1使用单向链表,我们需要定义两个特殊结点 :头结点-head,尾结点-last。由于链表是单向的,所以如果此时我们采用头插表示入队,复杂度可达到O(1);尾删表示出队,由于链表是单向的,所以还需要找到 last 结点的前一个结点,复杂度达到了O(N)。所以需要使用尾插表示入队,复杂度可达到O(1);头删表示出队,复杂度也可达到O(1).
方案二分析:如果采用方案2使用双向链表。由于链表是双向的,所以 无论是将头插表示出队,尾删表示入队;还是尾插表示入队,头删表示出队都可以达到复杂度为O(1).
2、Java集合中的 Queue
并且在Java集合中的Queue接口底层实现的就是一个双向链表:
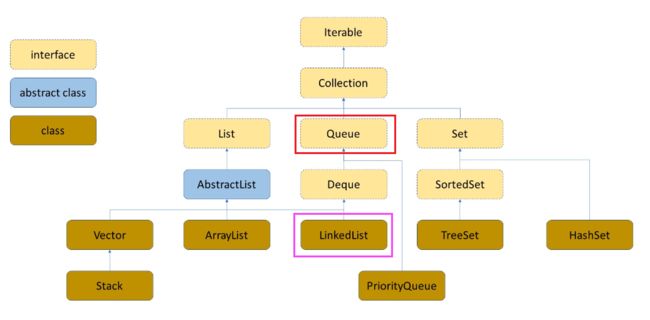
下面我们先查看一下Queue接口中一些常见的队列方法:
| 方法 | 功能 |
|---|---|
boolean offer(E e) |
入队列,将元素插入队列尾部 |
E poll() |
出队列,移除并返回队头元素 |
E peek() |
获取队头元素,但不移除 |
int size() |
获取队列中有效元素的个数 |
boolean isEmpty() |
检测队列是否为空 |
3、Queue 模拟实现
同样根据上面给出的队列方法,下面就实现一个底层为双向链表的队列,大家可以参照上述实现思路和代码注释进行理解:
//原理:先进先出
//思路:双向链表头尾无所谓,下面采用[头插、尾删]代替[入队、出队]
public class DQueue {
// 定义双向链表节点
static class Node {
public int val;
public Node prev;
public Node next;
public Node(int val) {
this.val = val;
}
}
// 头结点
public Node head;
// 尾结点
public Node last;
// 队列长度
public int size;
//1.入队列:boolean offer(E e) 【头插】
public boolean offer(int e) {
Node node = new Node(e);
// 判空
if (isEmpty()) {
head = node;
last = node;
} else {
// 头插
node.next = head;
head.prev = node;
head = head.prev;
}
size++;
return true;
}
//2.出队列:E poll() 【尾删】
public int poll() {
// 判空
if (isEmpty()) {
// 这里可以自定义异常
throw new EmptyException("队列为空!");
}
// 接收出队元素
int ret = head.val;
// 如果只有1个结点
if (head.next == null) {
last = null;
head = null;
} else {
// 大于1个结点
last.prev.next = null;
last = last.prev;
}
size--;
return ret;
}
//3.获取队头元素:int peek()
public int peek() {
// 判空
if (isEmpty()) {
// 这里可以自定义异常
throw new EmptyException("队列为空!");
}
return head.val;
}
//4.获取队列中有效元素个数:int size()
public int getSize() {
return size;
}
//5.检测队列是否为空:boolean isEmpty()
public boolean isEmpty() {
return size == 0;
}
}
六、设计循环队列
循环队列通过巧妙地利用数组的循环使用,解决了普通队列在头部插入和删除操作时效率低下的问题,使得offer()和poll()操作均能够在O(1)的时间复杂度内完成。这种结构经常在 生产者消费者模型(敬请期待) 中使用。
1、循环队列涉及的两个关键问题
循环队列的设计主要涉及两个关键问题:
- 数组下标如何循环?
- 如何判断循环队列的空与满?
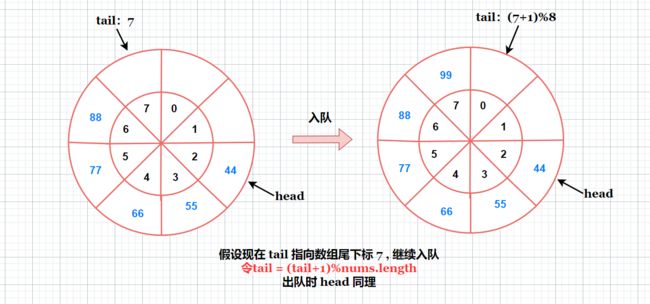
(1)问题 1 解决方案
方案一: 让 head 和 tail 使用加 1 取模操作。既保证当 head 和 tail 不处于数组尾下标时,加 1 取模操作不影响下标正常递增,又能保证 head 和 tail 处于数组尾下标时继续 入队 或 出队 下标循环。
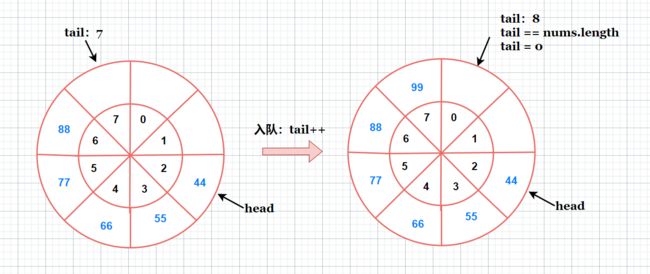
方案二: 判断 tail 和 head 与 数组长度 nums.length 是否相等,相等则置 0 保证下标循环。
(2)问题 2 解决方案
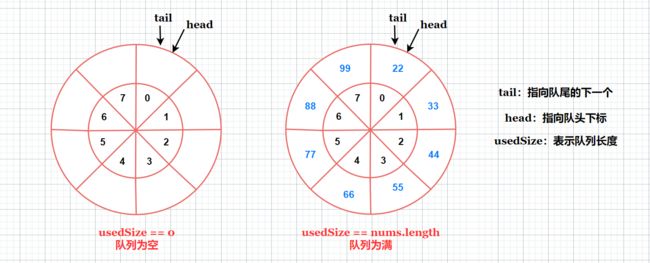
方案一: 设置 usedSize 变量记录队列元素个数。usedSize 为 0 队列为空;usedSize 等于数组长度 nums.length 队列为满。
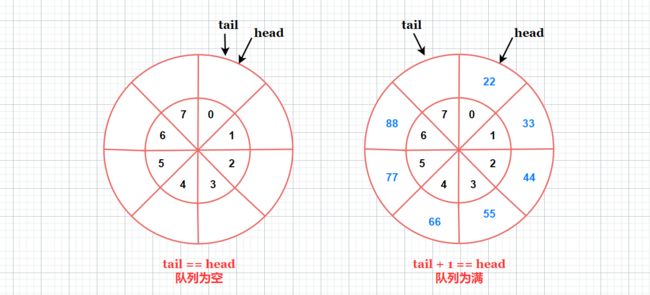
方案二: 牺牲 1 个数组元素。当 head 等于 tail 时表示队列为空;当 tail + 1 等于 head 时表示队列为满。
2、循环队列具体实现
解决了上面两个问题,下面的实现就是信手拈来。下面给出具体的实现代码,大家可以参照注释理解(判空 / 满 :这里采用 useSize;循环:使用 head / tail 与 nums.length 判断):
// 规定有效元素为:[head,tail)
// 判空判满使用:usedSize
// 下标循环使用:head / tail 与 nums.length 判断
public class CircularQueue {
// 数组
private int[] elem;
// 队头
private int head;
// 队尾的下一个
private int tail;
// 有效元素个数
private int usedSize;
// 使用构造方法,初始化循环队列
public CircularQueue(int k) {
this.elem = new int[k];
this.head = 0;
this.tail = 0;
this.usedSize = 0;
}
// 1.入队列:put()
public boolean put(int val) {
// 判满
if (isFull()) {
return false;
}
// 正常入队情况
elem[tail ++] = val;
// 增加有效元素个数
usedSize ++;
// 判断下标
if (tail == elem.length) {
tail = 0;
}
return true;
}
// 2.出队列:take()
public int take() {
// 判空
if (isEmpty()) {
throw new EmptyException("队列为空!");
}
// 正常出队情况
int val = elem[head ++];
// 减少有效元素个数
usedSize --;
// 判断下标
if (head == elem.length) {
head = 0;
}
return val;
}
// 3.获取队头元素:peekHead()
public int peekHead() {
// 判空
if (isEmpty()) {
throw new EmptyException("队列为空!");
}
int val = elem[head --];
return val;
}
// 4.获取队尾元素:peekTail()
public int peekTail() {
// 判空
if (isEmpty()) {
throw new EmptyException("队列为空!");
}
// 由于 tail 指向最后一个有效元素的下一个,所以需要考虑下标边界情况
int index = tail == 0? elem.length -1:tail -1;
int val = elem[index];
return val;
}
// 5.判空:isEmpty()
public boolean isEmpty() {
return usedSize == 0;
}
// 6.判满:isFull()
public boolean isFull() {
return usedSize == elem.length;
}
// 7.获取队列有效元素个数:getSize()
public int getSize() {
return usedSize;
}
}
七、Deque 集合类
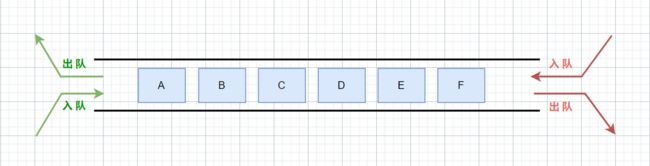
Deque表示一个双端队列,即允许两端都可以进行入队和出队操作的队列。
在Java集合框架中,Deque是一个接口,它实现了LinkedList和ArrayDeque,分别表示双端队列的线性实现 和 双端队列的链式实现。其中线性实现的底层为一个循环数组,链式实现的底层为一个双向链表。
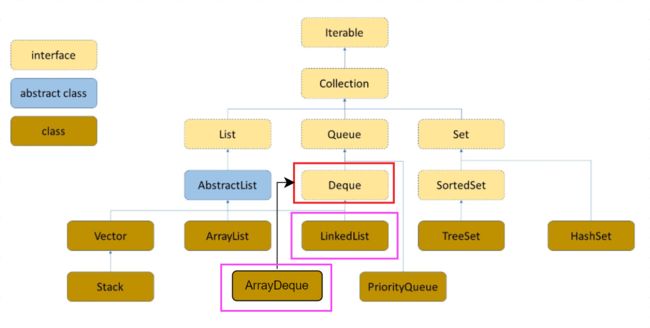
在实际工程中,使用Deque接口是比较多的,Deque接口中涵盖了队列和栈的功能接口,实现栈和队列均可以使用该接口:
Deque<Integer> stack1 = new ArrayDeque<>(); // 线性实现
Deque<Integer> stack2 = new LinkedList<>(); // 链式实现
Deque<Integer> queue1 = new ArrayDeque<>(); // 线性实现
Deque<Integer> queue2 = new LinkedList<>(); // 链式实现