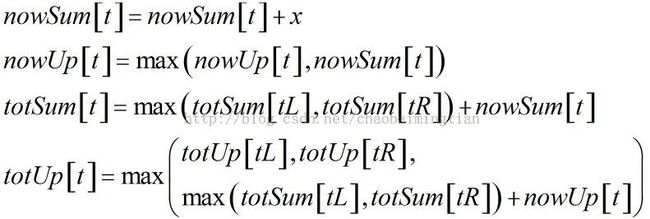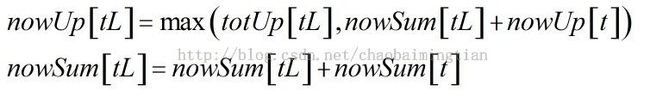SPOJ 1557 Can you answer these queries II(线段树)
题目链接:http://www.spoj.com/problems/GSS2/
题意:给出一个数列,每次询问区间[L,R]内最大的子段和。要求计算子段和时重复数字只能计算一次。
思路:(1)某个子段和必然是从某个位置j开始向前连续的一段。因此,我们首先将所有询问按照右区间升序,然后将数字一个一个插入线段树维护查询。由于重复数字只能计算一次,我们令pos[x]表示数字x上一次出现的位置,那么对于当前数字d[i],[pos[d[i]]+1,i]就是当前数字应该插入的区间。这样我们就解决了重复数字的问题。
(2)设从前向后插入,当前位置为curPos,对于某个查询[L,curPos],设最优子段的左开始端点为l,那么答案就是从l开始向右的某一段,为了能够维护这个值,我们在线段树节点t,[L,R]设置4个值nowSum,nowUp,totSum,totUp(其中sum[i,j]表示i到j不重复数字和):
上面的totUp就是每次查询的答案。每次在区间[L,R]插入数字x时进行维护(设当前节点t为[L,R],左右两个孩子tL,tR,[L,mid],[mid+1,R]):
最后就是向下传递是也就是我们经常用的pushDown函数:
tL的totSum和totUp与上面的一样,也是利用nowSum和nowUp以及左右孩子进行更新。tR跟tL一样。最后将t节点的nowSum和nowUp置为0。
struct node
{
i64 nowSum,nowUp,totSum,totUp;
int L,R;
};
node a[N<<2];
i64 d[N],ans[N];
int pos[N<<1],n,m;
struct Node
{
int L,R,id;
};
int cmp(Node a,Node b)
{
return a.R<b.R;
}
Node Q[N];
void build(int t,int L,int R)
{
a[t].L=L;
a[t].R=R;
a[t].nowSum=a[t].nowUp=a[t].totSum=a[t].totUp=0;
if(L==R) return;
int mid=(L+R)>>1;
build(t*2,L,mid);
build(t*2+1,mid+1,R);
}
void pushUp(int t)
{
if(a[t].L==a[t].R) return;
a[t].totSum=max(a[t*2].totSum,a[t*2+1].totSum)+a[t].nowSum;
a[t].totUp=max(a[t*2].totUp,a[t*2+1].totUp);
a[t].totUp=max(a[t].totUp,max(a[t*2].totSum,a[t*2+1].totSum)+a[t].nowUp);
}
void pushDown(int t)
{
if(a[t].L==a[t].R) return;
a[t*2].nowUp=max(a[t*2].nowUp,a[t*2].nowSum+a[t].nowUp);
a[t*2].nowSum+=a[t].nowSum;
a[t*2].totSum=a[t*2].nowSum;
a[t*2].totUp=a[t*2].nowUp>0?a[t*2].nowUp:0;
pushUp(t*2);
a[t*2+1].nowUp=max(a[t*2+1].nowUp,a[t*2+1].nowSum+a[t].nowUp);
a[t*2+1].nowSum+=a[t].nowSum;
a[t*2+1].totSum=a[t*2+1].nowSum;
a[t*2+1].totUp=a[t*2+1].nowUp>0?a[t*2+1].nowUp:0;
pushUp(t*2+1);
a[t].nowSum=a[t].nowUp=0;
}
void update(int t,int L,int R,i64 x)
{
if(a[t].L==L&&a[t].R==R)
{
a[t].nowSum+=x;
a[t].nowUp=max(a[t].nowUp,a[t].nowSum);
a[t].totSum=a[t].nowSum;
a[t].totUp=a[t].nowUp>0?a[t].nowUp:0;
pushUp(t);
return;
}
pushDown(t);
int mid=(a[t].L+a[t].R)>>1;
if(R<=mid) update(t*2,L,R,x);
else if(L>mid) update(t*2+1,L,R,x);
else
{
update(t*2,L,mid,x);
update(t*2+1,mid+1,R,x);
}
pushUp(t);
}
i64 query(int t,int L,int R)
{
if(a[t].L==L&&a[t].R==R) return a[t].totUp;
pushDown(t);
i64 ans;
int mid=(a[t].L+a[t].R)>>1;
if(R<=mid) ans=query(t*2,L,R);
else if(L>mid) ans=query(t*2+1,L,R);
else
{
ans=max(query(t*2,L,mid),query(t*2+1,mid+1,R));
}
pushUp(t);
return ans;
}
int get()
{
int x=0,p=1;
char c=getchar();
while(!isdigit(c)&&c!='-') c=getchar();
if(c=='-') p=-1,c=getchar();
while(isdigit(c))
{
x=x*10+c-'0';
c=getchar();
}
return x*p;
}
int main()
{
n=get();
int i;
FOR1(i,n) d[i]=get();
build(1,1,n); m=get();
FOR1(i,m) Q[i].L=get(),Q[i].R=get(),Q[i].id=i;
sort(Q+1,Q+m+1,cmp);
int j=1;
for(i=1;i<=n&&j<=m;i++)
{
update(1,pos[d[i]+S]+1,i,d[i]);
pos[d[i]+S]=i;
while(j<=m&&Q[j].R==i)
{
ans[Q[j].id]=query(1,Q[j].L,Q[j].R);
j++;
}
}
FOR1(i,m) PR(ans[i]);
}