极限学习机(ELM)的原理和matlab代码实现
单隐含层前馈神经网络(Single - hidden Layer Feedforward Neural Network,SLFN)以其良好的学习能力在许多领域得到了广泛的应用。然而,传统的学习算法(如 BP算法等)固有的一些缺点,成为制约其发展的主要瓶颈。前馈神经网络大多采用梯度下降方法,该方法主要存在以下几个方面的缺点和不足:
①训练速度慢。由于梯度下降法需要多次迭代,从而达到修正权值和阈值的目的,因此训练过程耗时较长。
②容易陷入局部极小点,无法达到全局最小。
③学习率η的选择敏感。学习率n对神经网络的性能影响较大,必须选择合适的n,才能获得较为理想的网络。若η太小,则算法收敛速度很慢,训练过程耗时较长;若n太大,则训练过程可能不稳定(收敛)。
因此,探索一种训练速度快,获得全局最优解且具有良好的泛化性能的训练算法是提升前馈神经网络性能的主要目标,也是近年来的研究热点和难点。
本篇博客将介绍一个针对SLFN 的新算法——极限学习机(Extreme Learning Machine,ELM),该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值,且在训练过程中无需调整,只需要设置隐含层神经元的个数,便可以获得唯一的最优解。与传统的训练方法相比,该方法具有学习速度快、泛化性能好等优点。
1 案例背景
1.1 极限学习机概述
典型的单隐含层前馈神经网络结构如图29-1所示,由输入层、隐含层和输出层组成,输入层与隐含层、隐含层与输出层神经元间全连接。其中,输入层有n个神经元,对应n个输入变量;隐含层有l个神经元;输出层有m个神经元,对应m个输出变量。为不失一般性,设输入层与隐含层间的连接权值w为
1.2 ELM的学习算法
由前文分析可知,ELM在训练之前可以随机产生w和b,只需确定隐含层神经元个数及隐含层神经元的激活函数(无限可微),即可计算出β。具体地,ELM的学习算法主要有以下几个步骤:
 值得一提的是,相关研究结果表明,在ELM中不仅许多非线性激活函数都可以使用(如S型函数、正弦函数和复合函数等),还可以使用不可微函数,甚至可以使用不连续的函数作为激活函数。
值得一提的是,相关研究结果表明,在ELM中不仅许多非线性激活函数都可以使用(如S型函数、正弦函数和复合函数等),还可以使用不可微函数,甚至可以使用不连续的函数作为激活函数。
1.3 问题描述
ELM以其学习速度快、泛化性能好等优点,引起了国内外许多专家和学者的研究与关注。ELM不仅适用于回归、拟合问题,亦适用于分类,模式识别等领域,因此,其在各个领域均得到广泛的应用。同时,不少改进的方法与策略也被不断提及,ELM的性能也得到了很大的提升,其应用的范围亦愈来愈广,其重要性亦日益体现出来。
为了评价ELM的性能,试分别将ELM应用于非线性函数拟合和乳腺肿瘤诊断两个问题中,并将其结果与其他方法的性能和运行速度进行比较,并探讨隐含层神经元个数对ELM性能的影响。
2 模型建立
2.1设计思路
依据问题描述中的要求,实现ELM的创建、训练及仿真测试,大体上可以分为以下几个步骤,如图29-2所示。
2.2 设计步骤
1)训练集/测试集产生
与传统前馈神经网络相同,为了使得建立的模型具有良好的泛化性能,ELM要求具有足够多的训练样本且具有较好的代表性。同时,训练集和测试集的格式应符合ELM训练和预测函数的要求。
2)ELM创建/训练
利用elmtrain()函数可以方便地创建、训练ELM,具体用法请参考第3节,值得一提的是,如前文所述,隐含层神经元个数对ELM的性能影响较大,因此,需要选择一个合适的隐含层神经元个数,具体讨论见第5节。
3)ELM仿真测试
利用elmpredict()函数可以方便地进行ELM的仿真测试,具体用法请参考第3节。
4)性能评价
通过计算测试集预测值与真实值间的误差(均方误差、决定系数、正确率等)可以对模型的泛化能力进行评价。同时,可以对比 ELM与传统前馈神经网络的运行时间,从而对ELM的运算速度进行评价。
3 极限学习机训练与预测函数
ELM的学习算法及步骤可以方便地在 MATLAB环境下实现。为了方便读者学习,使用ELM,编写了ELM的训练和预测函数,下面详细介绍它们的调用格式和具体函数内容。
3.1 ELM训练函数———elmtrain()
elmtrain()函数为ELM的创建、训练函数,其调用格式为:
[IW,B,LW,TF,TYPE] = elmtrain(P,T,N,TF,TYPE)
其中,P为训练集的输入矩阵;T为训练集的输出矩阵;N为隐含层神经元的个数(默认为训练集的样本数);TF为隐含层神经元的激活函数,其取值可以为'sig '(默认) ,' sin ',' hardlim ';TYPE为ELM的应用类型,其取值可以为0(默认,表示回归、拟合)和1(表示分类);IW为输人层与隐含层间的连接权值;B为隐含层神经元的阈值;LW为隐含层与输出层的连接权值。
elmtrain.m函数文件具体内容如下:
function [IW,B,LW,TF,TYPE] = elmtrain(P,T,N,TF,TYPE)
% ELMTRAIN Create and Train a Extreme Learning Machine
% Syntax
% [IW,B,LW,TF,TYPE] = elmtrain(P,T,N,TF,TYPE)
% Description
% Input
% P - Input Matrix of Training Set (R*Q)
% T - Output Matrix of Training Set (S*Q)
% N - Number of Hidden Neurons (default = Q)
% TF - Transfer Function:
% 'sig' for Sigmoidal function (default)
% 'sin' for Sine function
% 'hardlim' for Hardlim function
% TYPE - Regression (0,default) or Classification (1)
% Output
% IW - Input Weight Matrix (N*R)
% B - Bias Matrix (N*1)
% LW - Layer Weight Matrix (N*S)
% Example
% Regression:
% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',0)
% Y = elmtrain(P,IW,B,LW,TF,TYPE)
% Classification
% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',1)
% Y = elmtrain(P,IW,B,LW,TF,TYPE)
% See also ELMPREDICT
% Yu Lei,11-7-2010
% Copyright www.matlabsky.com
% $Revision:1.0 $
if nargin < 2
error('ELM:Arguments','Not enough input arguments.');
end
if nargin < 3
N = size(P,2);
end
if nargin < 4
TF = 'sig';
end
if nargin < 5
TYPE = 0;
end
if size(P,2) ~= size(T,2)
error('ELM:Arguments','The columns of P and T must be same.');
end
[R,Q] = size(P);
if TYPE == 1
T = ind2vec(T);
end
[S,Q] = size(T);
% Randomly Generate the Input Weight Matrix
IW = rand(N,R) * 2 - 1;
% Randomly Generate the Bias Matrix
B = rand(N,1);
BiasMatrix = repmat(B,1,Q);
% Calculate the Layer Output Matrix H
tempH = IW * P + BiasMatrix;
switch TF
case 'sig'
H = 1 ./ (1 + exp(-tempH));
case 'sin'
H = sin(tempH);
case 'hardlim'
H = hardlim(tempH);
end
% Calculate the Output Weight Matrix
LW = pinv(H') * T';
3.2 ELM预测函数——elmpredict()
elmpredict.m函数文件具体内容如下:
function Y = elmpredict(P,IW,B,LW,TF,TYPE)
% ELMPREDICT Simulate a Extreme Learning Machine
% Syntax
% Y = elmtrain(P,IW,B,LW,TF,TYPE)
% Description
% Input
% P - Input Matrix of Training Set (R*Q)
% IW - Input Weight Matrix (N*R)
% B - Bias Matrix (N*1)
% LW - Layer Weight Matrix (N*S)
% TF - Transfer Function:
% 'sig' for Sigmoidal function (default)
% 'sin' for Sine function
% 'hardlim' for Hardlim function
% TYPE - Regression (0,default) or Classification (1)
% Output
% Y - Simulate Output Matrix (S*Q)
% Example
% Regression:
% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',0)
% Y = elmtrain(P,IW,B,LW,TF,TYPE)
% Classification
% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',1)
% Y = elmtrain(P,IW,B,LW,TF,TYPE)
% See also ELMTRAIN
% Yu Lei,11-7-2010
% Copyright www.matlabsky.com
% $Revision:1.0 $
if nargin < 6
error('ELM:Arguments','Not enough input arguments.');
end
% Calculate the Layer Output Matrix H
Q = size(P,2);
BiasMatrix = repmat(B,1,Q);
tempH = IW * P + BiasMatrix;
switch TF
case 'sig'
H = 1 ./ (1 + exp(-tempH));
case 'sin'
H = sin(tempH);
case 'hardlim'
H = hardlim(tempH);
end
% Calculate the Simulate Output
Y = (H' * LW)';
if TYPE == 1
temp_Y = zeros(size(Y));
for i = 1:size(Y,2)
[max_Y,index] = max(Y(:,i));
temp_Y(index,i) = 1;
end
Y = vec2ind(temp_Y);
end
4.主函数和运行结果
4.1 分类问题主函数与运行结果
%% 极限学习机在分类问题中的应用研究
%% 清空环境变量
clear all
clc
warning off
%% 导入数据
load data.mat
% 随机产生训练集/测试集
a = randperm(569);
Train = data(a(1:500),:);
Test = data(a(501:end),:);
% 训练数据
P_train = Train(:,3:end)';
T_train = Train(:,2)';
% 测试数据
P_test = Test(:,3:end)';
T_test = Test(:,2)';
tic
%% ELM创建/训练
[IW,B,LW,TF,TYPE] = elmtrain(P_train,T_train,100,'sig',1);
%% ELM仿真测试
T_sim_1 = elmpredict(P_train,IW,B,LW,TF,TYPE);
T_sim_2 = elmpredict(P_test,IW,B,LW,TF,TYPE);
toc
%% 结果对比
result_1 = [T_train' T_sim_1'];
result_2 = [T_test' T_sim_2'];
% 训练集正确率
k1 = length(find(T_train == T_sim_1));
n1 = length(T_train);
Accuracy_1 = k1 / n1 * 100;
disp(['训练集正确率Accuracy = ' num2str(Accuracy_1) '%(' num2str(k1) '/' num2str(n1) ')'])
% 测试集正确率
k2 = length(find(T_test == T_sim_2));
n2 = length(T_test);
Accuracy_2 = k2 / n2 * 100;
disp(['测试集正确率Accuracy = ' num2str(Accuracy_2) '%(' num2str(k2) '/' num2str(n2) ')'])
%% 显示
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
rate_B = count_B / 500;
rate_M = count_M / 500;
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
number_B_sim = length(find(T_sim_2 == 1 & T_test == 1));
number_M_sim = length(find(T_sim_2 == 2 & T_test == 2));
disp(['病例总数:' num2str(569)...
' 良性:' num2str(total_B)...
' 恶性:' num2str(total_M)]);
disp(['训练集病例总数:' num2str(500)...
' 良性:' num2str(count_B)...
' 恶性:' num2str(count_M)]);
disp(['测试集病例总数:' num2str(69)...
' 良性:' num2str(number_B)...
' 恶性:' num2str(number_M)]);
disp(['良性乳腺肿瘤确诊:' num2str(number_B_sim)...
' 误诊:' num2str(number_B - number_B_sim)...
' 确诊率p1=' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊:' num2str(number_M_sim)...
' 误诊:' num2str(number_M - number_M_sim)...
' 确诊率p2=' num2str(number_M_sim/number_M*100) '%']);
R = [];
for i = 50:50:500
%% ELM创建/训练
[IW,B,LW,TF,TYPE] = elmtrain(P_train,T_train,i,'sig',1);
%% ELM仿真测试
T_sim_1 = elmpredict(P_train,IW,B,LW,TF,TYPE);
T_sim_2 = elmpredict(P_test,IW,B,LW,TF,TYPE);
%% 结果对比
result_1 = [T_train' T_sim_1'];
result_2 = [T_test' T_sim_2'];
% 训练集正确率
k1 = length(find(T_train == T_sim_1));
n1 = length(T_train);
Accuracy_1 = k1 / n1 * 100;
% disp(['训练集正确率Accuracy = ' num2str(Accuracy_1) '%(' num2str(k1) '/' num2str(n1) ')'])
% 测试集正确率
k2 = length(find(T_test == T_sim_2));
n2 = length(T_test);
Accuracy_2 = k2 / n2 * 100;
% disp(['测试集正确率Accuracy = ' num2str(Accuracy_2) '%(' num2str(k2) '/' num2str(n2) ')'])
R = [R;Accuracy_1 Accuracy_2];
end
figure
plot(50:50:500,R(:,2),'b:o')
xlabel('隐含层神经元个数')
ylabel('测试集预测正确率(%)')
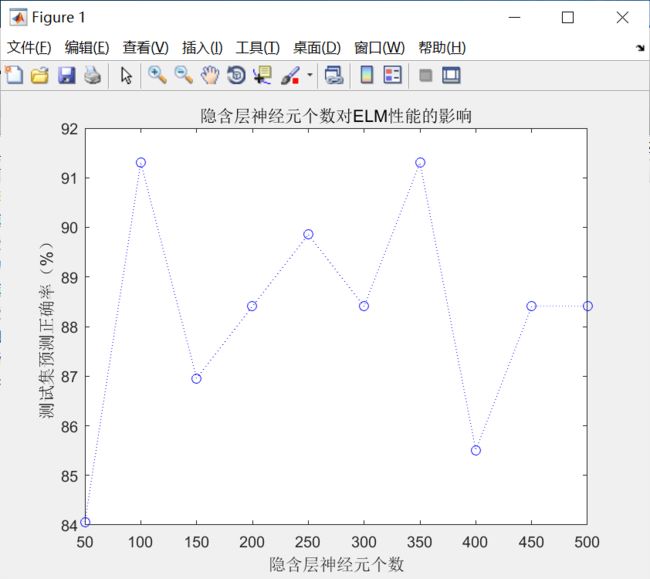
title('隐含层神经元个数对ELM性能的影响')
运行结果:
4.2 拟合问题主函数和运行结果
%% 极限学习机在回归拟合问题中的应用研究
%% 清空环境变量
clear all
clc
%% 导入数据
load data
% 随机生成训练集、测试集
k = randperm(size(input,1));
% 训练集——1900个样本
P_train=input(k(1:1900),:)';
T_train=output(k(1:1900));
% 测试集——100个样本
P_test=input(k(1901:2000),:)';
T_test=output(k(1901:2000));
%% 归一化
% 训练集
[Pn_train,inputps] = mapminmax(P_train,-1,1);
Pn_test = mapminmax('apply',P_test,inputps);
% 测试集
[Tn_train,outputps] = mapminmax(T_train,-1,1);
Tn_test = mapminmax('apply',T_test,outputps);
tic
%% ELM创建/训练
[IW,B,LW,TF,TYPE] = elmtrain(Pn_train,Tn_train,20,'sig',0);
%% ELM仿真测试
Tn_sim = elmpredict(Pn_test,IW,B,LW,TF,TYPE);
% 反归一化
T_sim = mapminmax('reverse',Tn_sim,outputps);
toc
%% 结果对比
result = [T_test' T_sim'];
% 均方误差
E = mse(T_sim - T_test)
% 决定系数
N = length(T_test);
R2 = (N*sum(T_sim.*T_test)-sum(T_sim)*sum(T_test))^2/((N*sum((T_sim).^2)-(sum(T_sim))^2)*(N*sum((T_test).^2)-(sum(T_test))^2))
%% 绘图
figure
plot(1:length(T_test),T_test,'r*')
hold on
plot(1:length(T_sim),T_sim,'b:o')
xlabel('测试集样本编号')
ylabel('测试集输出')
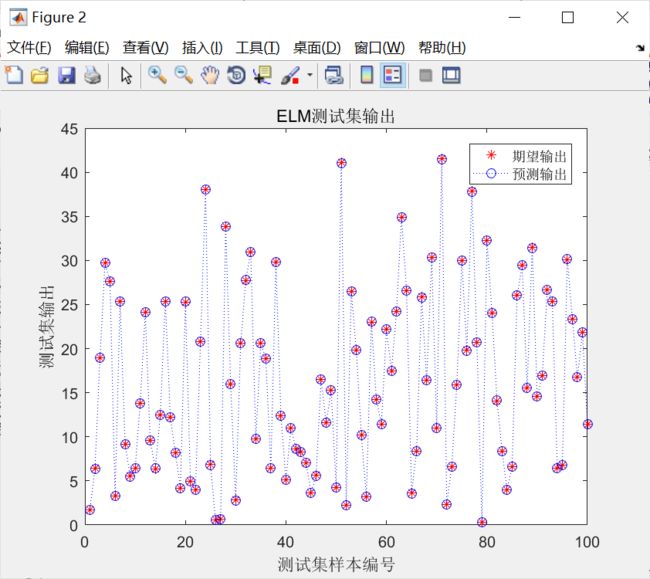
title('ELM测试集输出')
legend('期望输出','预测输出')
figure
plot(1:length(T_test),T_test-T_sim,'r-*')
xlabel('测试集样本编号')
ylabel('绝对误差')
title('ELM测试集预测误差')
运行结果如下:
 5.案例扩展
5.案例扩展
以乳腺肿瘤识别为例,探讨隐含层神经元个数的影响。从隐含层神经元个数对ELM性能的影响图可知,并非隐含层神经元个数越多越好,从测试集的预测正确率可以看出,当隐含层神经元个数逐渐增加时,测试集的预测正确率呈逐渐减小的趋势。因此,需要综合考虑测试集的预测正确率和隐含层神经元的个数,进行折中选择.
ELM以其学习速度快、泛化性能好、调节参数少等优点,在各个领域得到了广泛的应用。 随着研究的深人,一些专家提出了许多改进的方法,如在线学习ELM、进化ELM等,同时,一 些学者将其他算法中的思想(如SVM中的结构风险最小等)引入到ELM中,取得了不错的 效果。