遗传算法系列 | 多种群遗传算法(matlab)
多种群遗传算法 MPGA
本文是作者遗传算法系列之篇四,前面已经系统地讲解了遗传算法基本原理以及简单应用
系列一 —— 标准遗传算法原理及程序实现
系列二 —— 遗传算法应用于TSP问题
系列三 —— 遗传算法应用于车辆路径规划
不难发现,虽然遗传算法在一些简单问题上效果不错,但面对复杂的多模态函数时,常常发生早熟(未成熟收敛),也就是群体中所有个体都趋于同一状态而停止进化。
多种群遗传算法正是应对此问题的方法之一,下面将从理论原理、算法流程以及程序实现上进行详细展开。
00 目录
理论概述
算法流程
问题导入
MATLAB程序实现
展望
01 理论概述
多种群遗传算法(multiple population GA,MPGA)与标准遗传算法(SGA)的基础上主要引入了以下几个概念:
- 突破遗传算法仅靠单个群体进行遗传算法进化的框架,引入多个种群同时进行优化搜索;不同的种群赋予不同的控制参数,实现不同的搜索目的。
- 各个种群之间通过移民算子进行联系,实现多种群的协同进化;最优解的获取是多个种群协同进化的综合结果。
- 通过人工选择算子保存各种群每个进化代中 的最优个体,并作为判断算法收敛的依据。
具体来说
各种群取不同的控制参数,MPGA弥补了SGA依赖于交叉算子Pc、变异算子Pm的缺陷,通过设有不同控制参数的种群协同进化,从而兼顾算法的全局搜索和局部搜索。
各种群相对独立,种群交互通过移民算子联系。移民算子将各种群的最优个体定期引入其它种群中,实现种群之间的信息交换,这也是MPGA的特点所在。
精华种群和其它种群不同,每一代进化后,通过人工选择算子选出种群的最优个体放入精华种群,并且精华种群不进行选择、交叉、变异等操作,保证进化过程中最优个体不被破坏和丢失,并且精华种群的最优个体最少保持代数将作为算法终止判据,该判据充分利用了遗传算法在进化中的知识积累,较之最大遗传代数更为合理。
02 算法流程
算法流程与标准遗传算法相比,主要多出了移民和人工选择的操作,并且收敛条件也作了改变,MPGA流程图如下:

03 问题导入
3.1 问题描述
采用复杂的二元函数求最值问题,函数如下:
![]()
约束为:

该函数的图像如下所示:
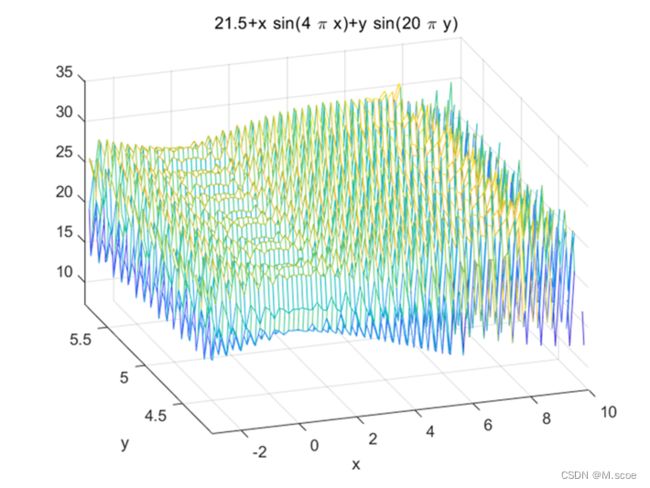
可以看出,该函数在取值范围内有大量局部极值,通常的寻优算法很容易陷入局部极值中或在极值间振荡,因此对于检验多种群遗传算法的性能是比较合适的。
3.2实验设计
为显示多种群遗传算法较之标准遗传算法的优越性,本文针对该函数,分别对两种算法做仿真对比,并分别独立运行4次观察其进化过程。
对于SGA部分,采用英国谢菲尔德大学推出的遗传算法工具箱,该工具箱在作者往期文章中可获取下载链接;(遗传算法工具箱地址)
对于MPGA部分,其主体部分和SGA大致相似,因此本文将重点介绍移民算子和人工选择算子的实现。
04 MATLAB程序实现
4.1 移民算子
该函数的代码如下
其中
输入参数的 Chrom 是移民前种群的编码, ObjV 是种群个体的适应度;
输出参数的 Chrom 是移民后种群的编码, ObjV 是种群个体的适应度。
移民算子的主要目的是将某一种群的优秀个体移到其它种群中
在此思想下,该段代码的思路:
- 获取种群数;
- 遍历每个种群,找到当前种群的最优个体以及目标种群的最劣个体;
- 将当前种群的最优个体替换到目标种群最劣个体位置;
- 更新适应度
- 结束
4.2 人工选择算子
该函数的代码如下
输入参数的Chrom是移民后种群的编码,ObjV是移民后种群个体的适应度,
MaxObjV是精英种群个体的适应度,MaxChrom是精英种群编码
输出参数的MaxChrom是选择后最优个体的编码,MaxObjV是最优个体的适应度。
人工选择算子的主要目的是将各个种群的最优个体提取出来组成精英种群
在此思想下,该段代码的思路:
- 获取种群数;
- 遍历每个种群,将移民后的种群最优个体适应度与精英种群相比,优胜劣汰;
- 结束
4.3 多种群遗传算法主程序
4.4 结果分析
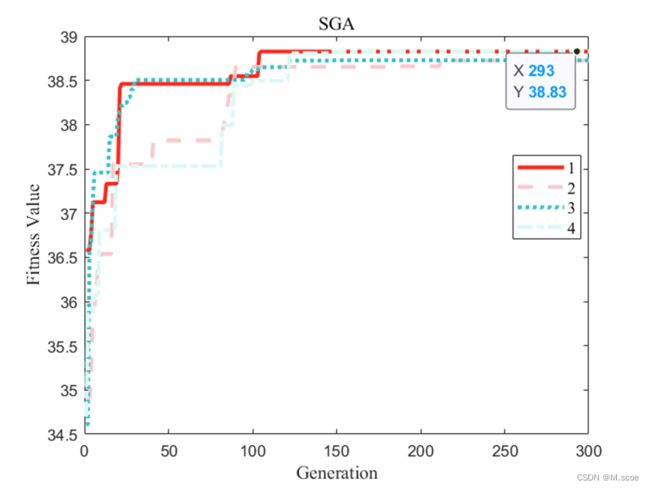
标准遗传算法运行4次的进化过程如图(a)所示
多种群遗传算法运行4次的进化过程如图(b)所示
由图(a)得知,多种群遗传算法运行4次的结果完全一致,且迭代次数小,平均在17次,基本没有陷入局部最优,说明****MPGA算法稳定性好,且收敛速度快,对于该多极值的函数问题较为适用;
而从图(b)可以看出,尽管迭代次数在300次时,SGA运行4次得到的优化结果仍不完全相同,显然第一次和第四次运行结果优于其余两次,说明算法会陷入局部最优解未成熟收敛现象,因此SGA算法稳定性较差,且有早熟收敛现情况,难以适用该问题。
05 展望
MPGA算法的优越在于采用了多个种群同时对解空间进行协同搜索,兼顾了算法的全局搜索和局部搜索,使得对遗传控制参数的敏感性降低,能够有效地克服未成熟收敛的现象。
同时,该思想同样能够用于其它类似的智能优化算法中,现在也有成功的应用,如多种群粒子群、多种群萤火虫等。
参考文献
[1]刘科研,盛万兴,马晓晨,李运华,董伟杰,杨丽曼.基于多种群遗传算法的分布式光伏接入配电网规划研究[J].太阳能学报,2021,42(06):146-155.DOI:10.19912/j.0254-0096.tynxb.2019-0370.
[2]刘鹏程,李新利.基于多种群遗传算法的含分布式电源的配电网故障区段定位算法[J].电力系统保护与控制,2016,44(02):36-41.
[3]郝翔,李人厚.适用于复杂函数优化的多群体遗传算法[J].控制与决策,1998(03):71-74.DOI:10.13195/j.cd.1998.03.71.haox.014.
最后,若想获取代码的伙伴,在评论区或者私信我你的邮箱,我如果看到了会发给你。
以上