最小生成树,prim算法
Prim算法和Kruskal算法都是用于解决最小生成树问题的经典算法,它们在不同情况下有不同的适用性和特点。
Prim算法:
Prim算法是一种贪心算法,用于构建一个无向图的最小生成树。算法从一个初始节点开始,逐步添加与当前树连接且具有最小权重的边,直到所有节点都被连接。Prim算法的基本思想是从一个起始节点出发,每次选择一个与当前最小生成树相连的节点中,权重最小的边,将这个节点加入最小生成树中,并将其相连的边考虑进来。这样逐步扩展最小生成树,直至所有节点都被包含。
Kruskal算法:
Kruskal算法也是一种贪心算法,用于构建一个无向图的最小生成树。该算法首先将图中的所有边按照权重从小到大进行排序,然后从最小权重边开始,依次将边加入生成树中,但要保证加入边不会形成环。如果加入某条边会导致环的形成,则放弃该边,继续考虑下一条权重较小的边,直到生成树中包含了所有的节点。
区别:
基本思想:Prim算法从一个起始节点开始,逐步添加与当前最小生成树相连的具有最小权重的边。Kruskal算法通过排序边,然后逐个添加边,保证不形成环。
顶点处理:Prim算法在每一步选择中,仅考虑与当前已选择顶点相连的顶点,直接操作顶点。Kruskal算法是通过遍历边的方式进行操作,不直接关心顶点。
数据结构:Prim算法通常使用优先队列(最小堆)来维护待选的边,以便每次选择具有最小权重的边。Kruskal算法则通常使用并查集来判断是否会形成环。
性能:在边的数量较少,而顶点的数量较多时,Prim算法通常会更有效。而在边的数量较多,而顶点的数量较少时,Kruskal算法可能更适用。
复杂度:Prim算法的时间复杂度通常在 O(V^2) 到 O(E* log(V)) 之间,取决于实现方式。Kruskal算法的时间复杂度主要由排序边的复杂度决定,通常为 O(E * log(E))。
总的来说,两种算法都能有效地构建最小生成树,但在不同情况下选择合适的算法可以提高效率。
1135. 最低成本联通所有城市
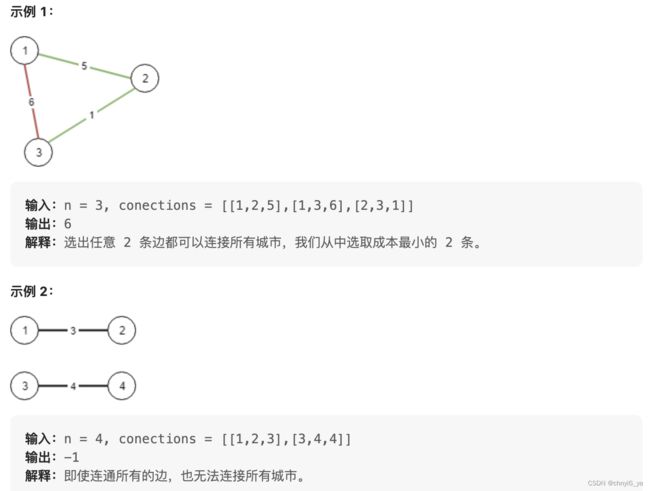
想象一下你是个城市基建规划者,地图上有 n 座城市,它们按以 1 到 n 的次序编号。
给你整数 n 和一个数组 conections,其中 connections[i] = [xi, yi, costi] 表示将城市 xi 和城市 yi 连接所要的costi(连接是双向的)。
返回连接所有城市的最低成本,每对城市之间至少有一条路径。如果无法连接所有 n 个城市,返回 -1
该 最小成本 应该是所用全部连接成本的总和。
// 定义边
struct Edge{
int city;
int cost;
};
// 定义 边的比较方法
// cost值较小的Edge对象具有更高的优先级,
// 因为EdgeComparator在a的cost大于b的cost时返回true,
// 这意味着在优先级队列中,a应该在b之后。
// 所以,这个优先级队列是一个最小堆(min heap),即队列顶部总是cost最小的Edge对象
struct EdgeComparator{
bool operator()(const Edge& a,const Edge& b){
return a.cost>b.cost;
}
};
class Solution {
public:
int minimumCost(int n, vector<vector<int>>& connections) {
// 连接所有点需要的cost
int cost = 0;
vector<vector<Edge>> edges(n+1);
// 定义访问数组
vector<bool> visited(n+1,false);
// 定义优先队列, cost小的排在前面
priority_queue<Edge, vector<Edge>, EdgeComparator> minHeap;
visited[1] = true;// 从城市1开始
// 建立Edge二维数组
// 每个点会对应一个list,每个list中存储:和这个点相连的城市以及到相连城市的距离
for(const auto& conn:connections){
// 是双向的
edges[conn[0]].push_back(Edge{conn[1],conn[2]});
edges[conn[1]].push_back(Edge{conn[0],conn[2]});
}
// 先把和1点相连的Edge进行排序,放入优先队列
for(const Edge& edge:edges[1]){
minHeap.push(edge);
}
// 连接点的数量,初始为1
int count = 1;
while(!minHeap.empty()){
Edge e = minHeap.top();
minHeap.pop();
if(visited[e.city]){
// 如果已经访问过某一点了,则直接进入下一次循环
continue;
}
// 如果没有访问过,就设置为true
visited[e.city] = true;
// 再把和这个点相连的Edge push进优先队列
for(const Edge& edge:edges[e.city]){
minHeap.push(edge);
}
cost += e.cost;
// 连接点的数量+1
count++;
if(count == n){
return cost;
}
}
return -1;
}
};
1584. 连接所有点的最小费用
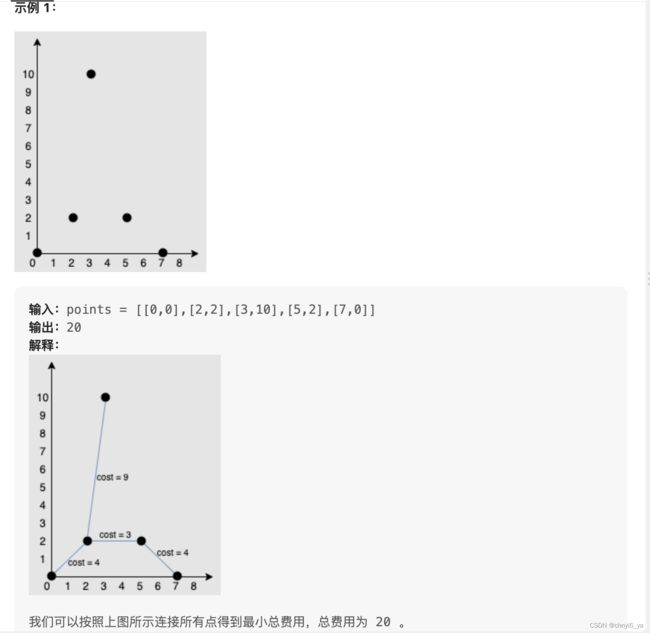
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
完全仿照上面一题的代码,写出了这题的代码,唯二的区别在于,需要自己额外计算一下每个点之间的距离,并且不满足条件时返回0:
// 定义结构体Edge
struct Edge{
int city;
int cost;
};
struct EdgeComparator{
bool operator()(const Edge& a,const Edge& b){
return a.cost>b.cost;
}
};
// 计算曼哈顿距离
int compute_Manhattan(vector<vector<int>>& points,int p1,int p2){
return abs(points[p1][0]-points[p2][0]) + abs(points[p1][1]-points[p2][1]);
}
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
int cost = 0;
int n = points.size();// 点的个数
vector<vector<Edge>> edges(n);
priority_queue<Edge, vector<Edge>, EdgeComparator> minHeap;
vector<bool> visited(n,false); // 访问数组
visited[0] = true; // 从0点开始search
int count = 1; // 已经访问到了的点(已经相连的点)
// 建立了 邻接表
for(int i = 0;i<n-1;i++){
for(int j = i+1;j<n;j++){
// 两点间的曼哈顿距离
int distance = compute_Manhattan(points,i,j);
edges[i].push_back(Edge{j,distance});
edges[j].push_back(Edge{i,distance});
}
}
// 把和0点相关的点push进最小堆
for(const Edge& edge:edges[0]){
minHeap.push(edge);
}
while(!minHeap.empty()){
Edge e = minHeap.top();
minHeap.pop();
if(visited[e.city]){
// 如果已经访问过该点,则进入下一次循环
continue;
}
visited[e.city] = true; // 标记访问过该点
// 再把和该点相连的点push 进 minHeap
for(const Edge& edge:edges[e.city]){
minHeap.push(edge);
}
cost += e.cost; // 加上和这个点相连的cost
count++;
if(count == n){
// 如果n个点都相连了,返回cost即可
return cost;
}
}
return 0;
}
};