有一种美叫朦胧的美
似花不是花,似雾不是雾!常言道:距离产生美,其背后的实质是距离产生模糊感,而模糊产生美感。本文将由我来细细阐述模糊的由来。
如上图,对图片的局部部分加以模糊,会使图片的整体视觉美感有一个大大的提升。那么为了达到这一效果,在图片的背后是如何去实现的呢?
图片背后的秘密
通常我们说到图片时,总会涉及图片的尺寸大小,如1080x1920、512x320等等,这里提到的数字,如1080x1920就说明这张二维图片:每行有1080个像素点,每列有1920个像素点。
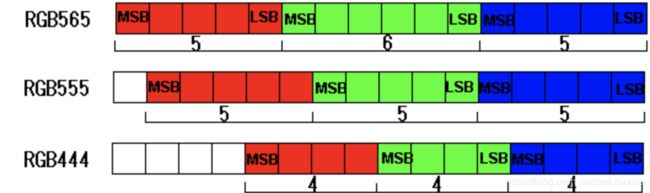
RGB红、绿、蓝三色根据不同比例的混合,可以形成多种多样的颜色,也充分显示了图片当中的各个细节。
而每个像素点通常是RGBA三个颜色通道加透明度组成,通常组合有RGB565、RGB888等,如RGB565表示每个像素点由5bit的R、6bit的G和5bit的B组成,也就是这个像素16bit两字节大小;最终这张图片的大小就是1080x1920x2字节,也就是3M多,这样原封不动的存储,是很消耗内存的。
为了尽可能的缩小其占用空间,根据图片像素点的相关性,以及视觉对一些颜色的敏感程度不同,采用不同的压缩算法,减小图片的像素点、以及像素点大小,对图片进行压缩,会使图片占用内存减少至1M甚至几百k,这样使用了不同压缩算法压缩后的图片,就有了jpg、jpeg、png等多种格式图片。
模糊的秘密
我们知道,图片上各式各样的图案都是像素点构成的,而每个像素点是由RGB不同比例组合来表达这些图案的细节,当我们改变这些RGB的不同比例也就会对图片表达进行改变;比如某个像素点RGB为100时,代表红色,那么我们将RGB改为95,它就变成淡红色,这样图片看起来和以前看起来不一样,没有很准确的反应图片细节,从而达到一个模糊的效果;所谓图片模糊,实质就是一个数据平滑技术。
如何模糊?
我们知道了图片模糊实质就是数据平滑技术,那么我们应该以哪种根据、规律来对图片的每个像素去修改,简而言之就是我们最终要怎么去修改每个像素点大小?
平均数模糊
简单的处理方法,以当前像素点为原点,取原点周围3x3大小矩阵的像素点值,对其求平均,结果为当前点的像素值;为什么这么做,应该图片中相邻像素点都是有相关性的,也就是相邻像素点也能够反应当前像素的细节,他们之间的差异不大,所以最终求出的结果也能够反应当前像素,而不会和当前像素相差太大;当我们取的矩阵越大,如5x5、7x7等,丢失的细节越严重,模糊的效果越明显。
高斯模糊
首先,平均数模糊通过周围像素点平均来计算合理吗?
显然是不合理的,根据相关性来说,计算当前像素点值时,离我近的像素应该和我相关性大一些,离我远的相关性要小一些,所以根据这一特性,推送出一个新算法,大致如下:
当 前 像 素 点 值 = 附 近 像 素 点 ∗ 权 重 0 + 远 处 像 素 点 ∗ 权 重 1 当前像素点值 = 附近像素点*权重0 + 远处像素点*权重1 当前像素点值=附近像素点∗权重0+远处像素点∗权重1
注意:权重0 > 权重1
大体思路如上,但是要如何确定不同像素的权重是多少呢,有没有一个函数能根据远近关系自动为附近每个像素点计算出权重呢?答案是有的!
高斯函数由誉为数学王子美称的高斯发明(可以百度了解下,确实很厉害),如下二维高斯函数:
G ( x , y ) = 1 2 π σ 2 e − ( x 2 + y 2 ) 2 σ 2 G(x,y) = \frac{1}{2πσ^2} e^-\frac{(x^2+y^2)}{2σ^2} G(x,y)=2πσ21e−2σ2(x2+y2)
其中σ是方差,方差反应了样本的离散程度,方差越大,说明样本数据离散越大,反之则越小,比较集中;二维函数图像如下:

有了这一函数以后,同时我们还要选择计算矩阵的大小,也就是:计算当前像素点,附近像素点参与计算的像素点多少,可以选择3x3、5x5、7x7等大小的矩阵,矩阵越大,参与计算的值越多,图像效果越模糊,再用我们的高斯函数计算矩阵中每个像素的权重值,就可以计算了,以下是c语言版本3x3的矩阵权重计算:
#define N 1
#define PI 3.141592653
int main()
{
double a[2 * N + 1][2 * N + 1]; // 计算矩阵;
double r = 1; // 高斯方差;
double A = 1 / (2 * PI * r * r);
cout << "方差半径r:" << r <<endl;
for (int i = -1 * N; i <= N; i++)
{
for (int j = -1 * N; j <= N; j++)
{
a[i + N][j + N] = A*exp((-1)*(i*i + j*j) / (2 * r*r));
//小数点后6位的精度
cout << setiosflags(ios::fixed) << setprecision(6) << a[i + N][j + N] << " ";
}
cout << endl;
}
return 0;
}
数据结果:
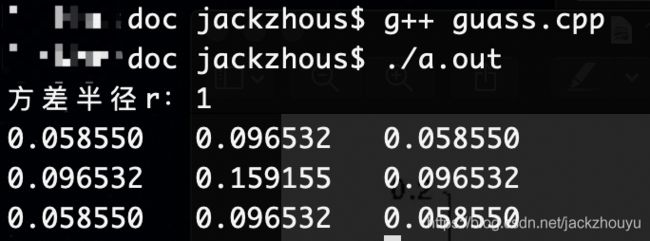
计算结果离中心点越近,权重越大,越远,权重越小,这就是我们要求的结果!
高斯模糊OpenGL实现
本例子使用相机Camera预览输出至SurfaceTexture,然后对SurfaceTexture的纹理重新渲染至FBO,渲染时shader使用了高斯模糊,最后在输出到TextureView;shader采用了高斯权重计算的思想,没有使用for循环去遍历计算矩阵的所有值,指定选择了周边附近的像素,进行权重计算,减少GPU的计算次数;为了达到模糊的效果,opengl实现高斯模糊算法大致有两个方向:
- 尽可能使用大的计算矩阵来计算结果,以达到模糊效果
- 对一张图片多次使用上面的方式进行模糊,以达到模糊效果
万变不离其宗,最终都是要实现权重计算,以下是我的例子shader:
vertex shader
attribute vec4 aPosition;
attribute vec4 aTextureCoord;
varying highp vec2 blurtexCoor[13];
uniform float xStep;
uniform float yStep; //归一化后每个步长
void main(){
gl_Position = aPosition;
blurtexCoor[0] = aTextureCoord.xy;
//乘2是因为步长太短 像素可能没什么变化
blurtexCoor[1] = aTextureCoord.xy + vec2(xStep, 0.0);
blurtexCoor[2] = aTextureCoord.xy + vec2(-xStep, 0.0);
blurtexCoor[3] = aTextureCoord.xy + vec2(0.0, yStep);
blurtexCoor[4] = aTextureCoord.xy + vec2(0.0, yStep);
blurtexCoor[5] = aTextureCoord.xy + vec2(xStep, yStep);
blurtexCoor[6] = aTextureCoord.xy + vec2(-xStep, -yStep);
blurtexCoor[7] = aTextureCoord.xy + vec2(xStep*2.0, 0.0);
blurtexCoor[8] = aTextureCoord.xy + vec2(-xStep*2.0, 0.0);
blurtexCoor[9] = aTextureCoord.xy + vec2(0.0, yStep*2.0);
blurtexCoor[10] = aTextureCoord.xy + vec2(0.0, yStep*2.0);
blurtexCoor[11] = aTextureCoord.xy + vec2(xStep*2.0, yStep*2.0);
blurtexCoor[12] = aTextureCoord.xy + vec2(-xStep*2.0, -yStep*2.0);
}
fragment shader:
// 上中下屏幕分割 上下高斯模糊 中间原图
precision highp float;
uniform sampler2D inputTexture; // 原始图像
varying highp vec2 blurtexCoor[13];
void main() {
lowp vec4 color = vec4(0.0);
if(blurtexCoor[0].y < 0.7 && blurtexCoor[0].y > 0.3){
color = texture2D(inputTexture, blurtexCoor[0]);
}else{
color = texture2D(inputTexture, blurtexCoor[0]) * 0.3;
color += texture2D(inputTexture, blurtexCoor[1]) * 0.12;
color += texture2D(inputTexture, blurtexCoor[2]) * 0.12;
color += texture2D(inputTexture, blurtexCoor[3]) * 0.07;
color += texture2D(inputTexture, blurtexCoor[4]) * 0.07;
color += texture2D(inputTexture, blurtexCoor[5]) * 0.06;
color += texture2D(inputTexture, blurtexCoor[6]) * 0.06;
color += texture2D(inputTexture, blurtexCoor[7]) * 0.04;
color += texture2D(inputTexture, blurtexCoor[8]) * 0.04;
color += texture2D(inputTexture, blurtexCoor[9]) * 0.03;
color += texture2D(inputTexture, blurtexCoor[10]) * 0.03;
color += texture2D(inputTexture, blurtexCoor[11]) * 0.03;
color += texture2D(inputTexture, blurtexCoor[12]) * 0.03;
}
gl_FragColor = color;
}
最终的图像效果:
项目代码 tag为guass的位置是当前项目代码
高斯模糊的应用
高斯函数在很多地方都有用到,如统计学、自然科学、社会科学、数学等领域都有高斯函数的影子;比如在数学领域,高斯函数在埃尔米特多项式的定义中起着重要作用,可见高斯对现代理论是很重要的一个奠基人,再次膜拜一下!在图像领域,高斯函数可以应用于模糊,不仅如此,很多美颜算法、噪声消除都会用到高斯函数,这些在后续的学习中在一一道来!
![]()
