OpenGL ES学习教程 --- 坐标系统变换
OpenGL ES学习教程 — 坐标系统变换
简介
经过前面几节的学习,我们能画一个简单的图像,并且也可以上一些颜色,但是如果我们需要在2维屏幕上画一个3维图像,这就需要对物体坐标进行变换,3维是有XYZ轴的,而屏幕上的坐标只有XY轴(OpenGL的屏幕坐标称为归一化坐标,也有Z轴只是屏幕上的物体Z轴为0),那3维坐标转换为二维坐标的过程是如何实现的呢?这就是今天的主题
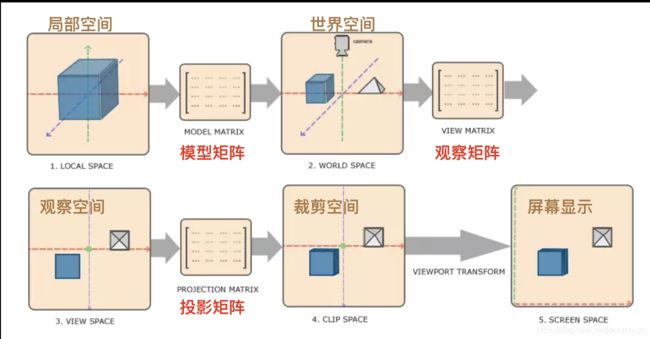
坐标系统转换图
一个三维物体最终转换到归一化坐标上去,大致会经过以下几个过程(借用大神的图):
4个空间3个矩阵
每个空间的坐标系是不同的,空间转换实质就是坐标转换,通过矩阵左乘(线性代数)坐标实现空间的转换,不用担心矩阵如何生成以及矩阵怎么去左乘,这些在OpenGL ES的提供的Matrix类帮我们实现,我们只需要掌握他的原理即可:
局部空间
OpenGL的原点(0,0,0)绘制的一个物体,任何物体都是以这个为基础进行坐标定位
世界空间
与局部空间类似,也是在OpenGL原点进行绘制,这个空间存在很多物体,可能许多物体重合在一块,我们可以通过translate、rorate防止重合
观察空间
世界空间的所有物体摆放好后,假设在某个位置摆放一个相机,从这个相机视角(叫做视点)观察出的所有物体,这个空间就叫观察空间;观察空间的坐标不在是OpenGL坐标了,它的坐标是以相机位置为原点(0,0,0)而产生的坐标系,那么它的XYZ轴如何确定呢?
推导观察空间坐标系
这里直接复制大神的推导过程,看之前你最好先复习下什么是向量、法向量、向量乘积和向量的叉乘:
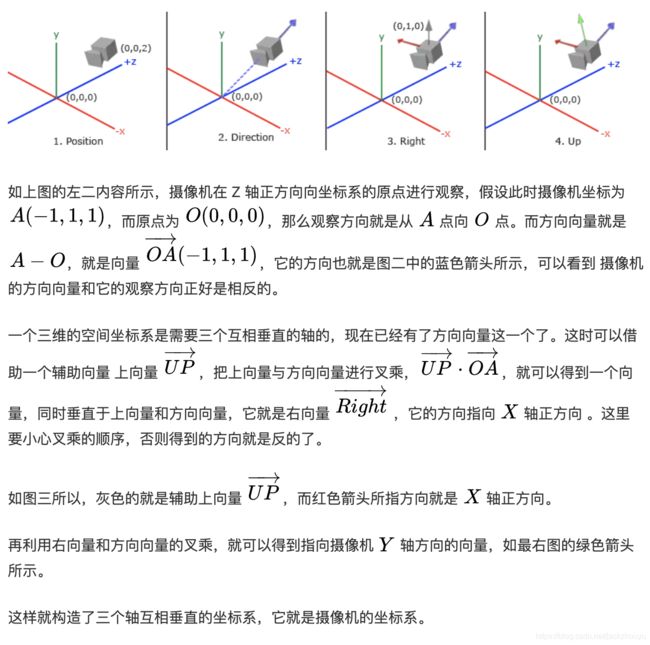
而在实际开发中,我们只需要使用Matrix.setLookAtM函数,他帮助我们实现观察矩阵,左乘就能够进行空间转换,这个矩阵实质就是上面推导内容推导出来的
public static void setLookAtM(float[] rm, int rmOffset,
float eyeX, float eyeY, float eyeZ,
float centerX, float centerY, float centerZ,
float upX, float upY,float upZ )
参数解释:
rm: 生成的观察矩阵
rmOffset : 矩阵偏移
eyeX、eyeY、eyeZ:相机的位置,相对于OpenGL坐标原点
centerX、centerY、centerZ:相机观察的点的位置
upX、upY、upZ:推导过程中的向上的辅助量,这3个参数如理解不好可以点这里
裁剪空间
因为OpenGL规定在屏幕上的坐标范围是【-1,1】的,超过这个范围是无法显示,所以需要一个裁剪矩阵对图像物体进行裁剪,那如何确定物体的哪些部分可以裁剪,哪些不能裁剪呢?
投影
由观察空间到裁剪空间在公式上左乘一个投影矩阵,这个投影矩阵的产生分为两种:正交投影和透视投影,不管是正交投影还是透视投影,最终都是将视景体内的物体投影在近平面上,这也是 3D 坐标转换到 2D 坐标的关键一步。
正交投影
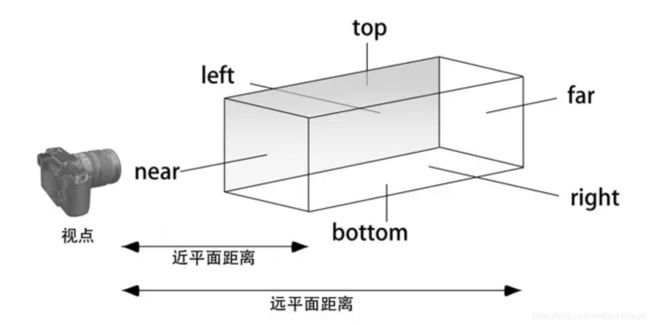
正交投影产生的效果无论你离物体多远多近,都不会产生近大远小的效果,大致如下图,视点作为观察点,视椎体由前后左右上下6个面包裹而成,物体在视椎体内部,最后投影到near近平面,视椎体范围之外将无法显示到屏幕上来
正交投影矩阵,由Matrix.orthoM这个方法产生
public static void orthoM(float[] m, int mOffset,
float left, float right, float bottom, float top,
float near, float far)
可以把近平面看作屏幕,left、right、top、bottom都是以近平面中心相对的距离,由于手机屏幕的长宽一般不相等,以短边为基准1,长边取值为长/宽,所以如果一个竖屏的手机使用这个正交投影产生的矩阵应该是:
float ratio = (float)height / width;
Matrix.orthoM(projectMatrix,0,-1, 1, -ratio, ratio, 1, 6);
透视投影
透视投影会产生近大远小的效果,产生的视椎体如下图:
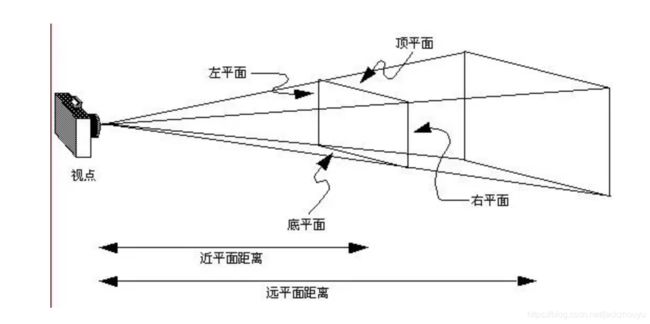
他也有响应的函数产生投影矩阵:
Matrix.frustumM(float[] m, int offset, float left, float right, float bottom, float top, float near, float far);
其参数意义同上一个orthM一样,使用投影矩阵后就转换到了裁剪空间去了,归一化坐标可以直接把图形画在OpenGL坐标屏幕上去
总结
经过上述的讲解,我们要完成4个空间转换,需要用到了3个转换矩阵:
- 从局部空间转换到世界空间,我们需要用到模型矩阵ModeMatrix,这个矩阵就是我们通常对物体进行translate、rorate换后产生的矩阵
- 从世界空间到观察空间,我们需要用到观察矩阵ViewMatrix,这个矩阵可以setLookAt方法帮我们生成
- 从观察空间到裁剪空间,我们可以用到投影矩阵ProjectMatrix,使用orthM、frustuM还有一个perspectiveM方法产生投影矩阵
- 最后以上几个坐标依次左乘我们的定义的坐标Position就可以得到归一化坐标了
- 所以,总结出来的公式
gl_Position = ProjectMatrix * ViewMatrix * ModeMatrix * g_Position
最后,也献上我学习此过程练习的demo