插入排序优化——超越归并排序的超级算法

插入排序算法

在了解如何改进插入排序之前，我们先要了解插入排序的基本算法：

算法讲解

插入排序对于少量元素的排序，是一个有效的算法 。

插入排序是一种简单的排序方法，它是将一个数据插入到已经排好序的有序数组，从而形成一个新的有序数组。

插入排序的工作方式像许多人排序扑克牌：

我们每次从桌子上拿走一张牌并将其插入到手中正确的位置。

为了找到它的正确位置，我们从右到左将它与手中的每张牌进行比较。

因此，手上的牌总是有序。

数据模拟

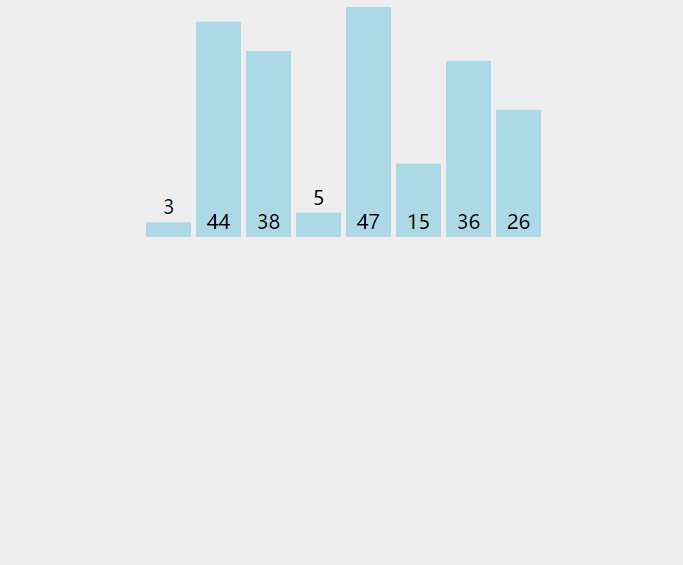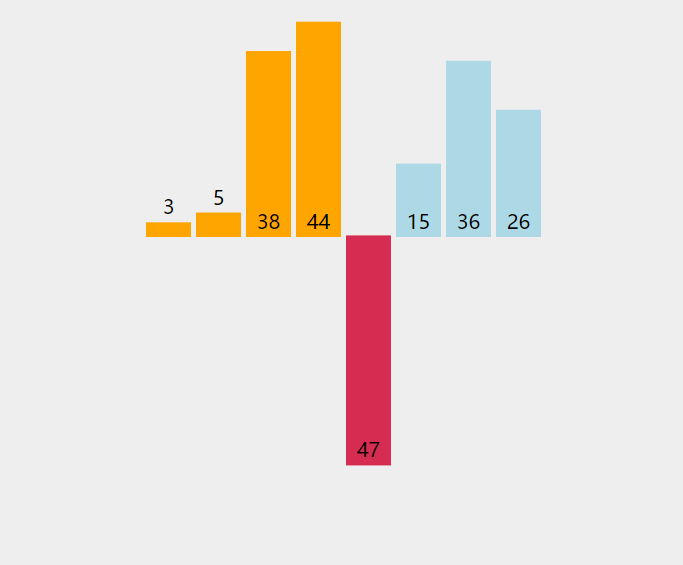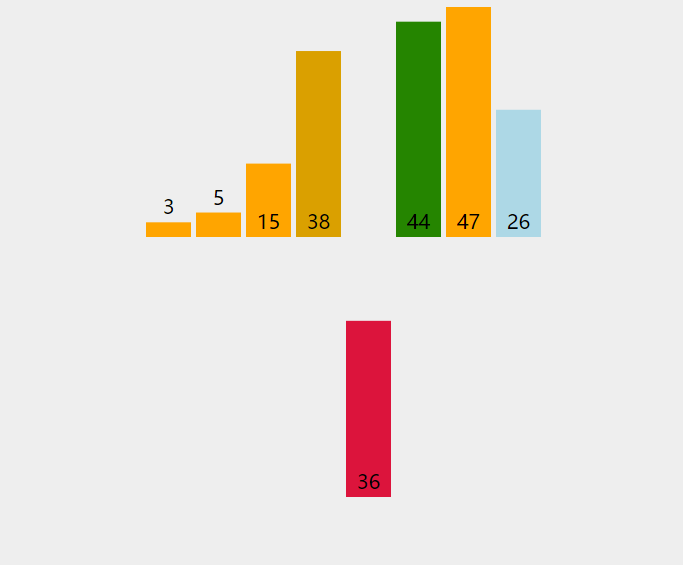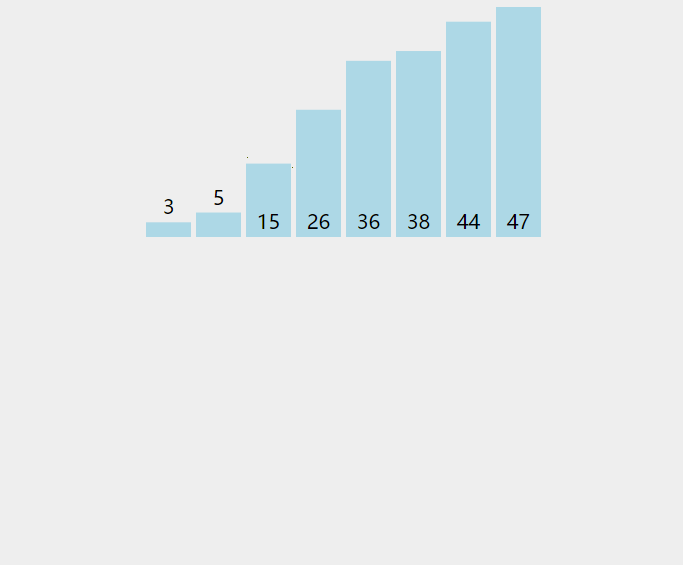
原本要排序的数为 5 3 4 2 9 1，从小到大排序。

3 5 4 2 9 1        // 将3放到合适的位置（5前面）

3 4 5 2 9 1        // 将4放到合适的位置（3、5中间）

2 3 4 5 9 1        // 将2放到合适的位置（最前面）

2 3 4 5 9 1        // 将9放到合适的位置（最后面）

1 2 3 4 5 9        // 将1放到合适的位置（最前面）

排序结束！！！

代码

#include 
using namespace std;
int n,a[2000];        //定义数据个数n，排序数组a
int main()
{
	cin >>n;        //输入个数
	for (int i=1;i<=n;i++)
		cin >>a[i];            //输入数据
    
	for (int i=2;i<=n;i++)    //第一个数本身只有一个元素，所有有序，因此不用参与排序
	{
		int j,k=a[i];        //记录下当前元素
		for (j=i-1;j>0;j--)
		{
			if (a[j]>k)        //若前面一个数大于当前元素
				a[j+1]=a[j];    //则将前面一个元素往后移动
			else
				break;        //否则：说明当前元素已经找到了合适的位置，推出循环
		}
		a[j+1]=k;        //将当前元素放入数组的合适的位置
        
		/*                        输出排序的过程
		for (int j=1;j<=n;j++)
			cout <
	}
    
	for (int i=1;i<=n;i++)
		cout <<a[i] <<" ";        //输出排序好的数组
	return 0;
}

优化思路

我们发现，插入排序的过程浪费在了查找合适的位置上，那么怎么优化呢？

我们知道，插入排序一直在维护 前$i$个数是有序的，那么如何快速在有序的数列中查找一个小于（或大于）自己的数呢？

一、二分查找

二分！！！！

那么这样我们就讲查找的时间从$O(n)$缩短为$O(nlog(n))$！！

忍不住激动！！

可是找到位置不够，还要进行移动啊。移动的时间复杂度是$O(n)$那么这样非但没有优化，反而还增加了查找的时间。。。

希望瞬间破灭！！

但是我会向它屈服吗？？？

会 吗？

明显不会！

二、copy函数

我们可以使用一个$STL$库里面的一个函数：

copy(a,a+n,a+1);

$copy$函数！！

这个函数可以在$O(1)$的时间范围内将数组的某一段移动到，
使用方法：
以上面的操作为例子，这表明：

• 以$a$数组的第$0$位为开头
• 以$a$数组的第$n-1$位位结尾
• 将它移动到开头位第$1$位的位置

那么，这就好办了，只需要要讲两个结合起来，一个速度与归并排序相当，代码比归并排序简短许多的超级优化插入排序代码诞生了：

优化后代码

#include 
#define N 2000000
using namespace std;
int n,x,y,f,t[N],k[N];
int main() {
	scanf("%d",&n);
	for (int i=1; i<=n; i++) {
		scanf("%d",&x);
		f=upper_bound(t+1,t+i,x)-t;		//记录二分的位置
		copy(t+f,t+i,t+f+1);	//copy
		t[f]=x;		//存入数组
	}
	for (int i=1; i<=n; i++) {
		printf("%d ",t[i]);
	}
	return 0;
}

输入数据：

5
4 9 1021 54 3

输出数据：

3 4 9 54 1021

也是对了好吧~~

算法的用途

这个算法可以快速的在有序数列里面进行操作，也是异常的方便快捷，代码超级简短！！
下面给一道可以用这个算法解决的问题：

题目：数星星（POJ2352 star）

天文学家经常观察星象图。星象图中用平面上的点来表示一颗星星，每一颗星星都有一个笛卡尔坐标。设定星星的等级为其左下角星星的总数。天文学家们想知道星星等级的分布情况。

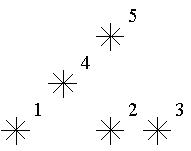
比如上图，$5$号星星的等级为$3$（其左下角有编号为$1$、$2$、$4$星星共三颗）。$2$号星星和$4$号星星的等级为$1$。在上图中只有一颗星星等级为$0$，两颗星星等级为$1$，一颗星星等级为$2$，一颗星星等级为$3$。
给定一个星象图，请你写一个程序计算各个等级的星星数目。

输入输出格式

输入格式：

输入的第一行包含星星的总数$N(1<=N<=15000)$。接下来$N$行，描述星星的坐标$(X,Y)$（$X$和$Y$用空格分开，$0\le X,Y\le 32000$）。星象图中的每个点处最多只有一颗星星。所有星星按$Y$坐标升序排列。$Y$坐标相等的星星按$X$坐标升序排列。

输出格式

输出包含$N$行，每行一个整数。第一行包含等级$0$的星星数目，第二行包含等级$1$的星星数目，依此类推，最后一行包含等级为$N-1$的星星数目。

输入输出样例

输入样例

5
1 1
5 1
7 1
3 3
5 5

输出样例

1
2
1
1
0

题目讲解

由于输入数据有序，所以在第$i$颗星星左下角的星星一定在$i$前面！！原理自己想想就知道了~~

所以其实就是求在点$i$前面的点中，有多少个的$X$坐标是比$i$的$X$坐标要小的，因此直接考虑插入排序做法：

步骤如下

• 输入星星的数量 $n$
• 循环从$1$到$n$

• 每次输入当前点的$X$和$Y$
• 用二分查找当前点的$X$应当放在哪个位置
• 用变了量$f$记录位置，$f-1$就是当前星星的等级
• 用$copy$将数据，从当前合适的位置开始，到$i-1$往后移动一位
• 将当前数据存入排序数组
• 用另一个数组标记这个等级的星星$++$

• 循环输出每个级别的星星

AC 代码

#include 
#define N 20000
using namespace std;
int n,x,y,f,t[N],k[N];
int main() {
	scanf("%d",&n);
	for (int i=1; i<=n; i++) {
		scanf("%d%d",&x,&y);
		f=upper_bound(t+1,t+i,x)-t;
		copy(t+f,t+i,t+f+1);
		t[f]=x;
		k[f-1]++;
	}
	for (int i=0; i<n; i++) {
		printf("%d\n",k[i]);
	}
	return 0;
}