_0x4c9738 怎么还原？嘿，还真可以还原！

_0x4c9738 变量名还原，噂嘟假嘟？

代码混淆（obfuscation）和代码反混淆（deobfuscation）在爬虫、逆向当中可以说是非常常见的情况了，初学者经常问一个问题，类似 _0x4c9738 的变量名怎么还原？从正常角度来说，这个东西没办法还原，就好比一个人以前的名字叫张三，后来改名叫张四了，除了张四本人和他爸妈，别人根本不知道他以前叫啥，类似 _0x4c9738 的变量名也一样，除了编写原始代码的人知道它原来的名称是啥以外，其他人是没办法知道的。

然而，_0x4c9738 就真的没办法还原吗？时代在进步，这几年人工智能蓬勃发展，在机器学习的加持下，让变量名的还原也成为了一种可能。本文将介绍三种还原的方法：ChatGPT、JSNice 和 JSNaughty。

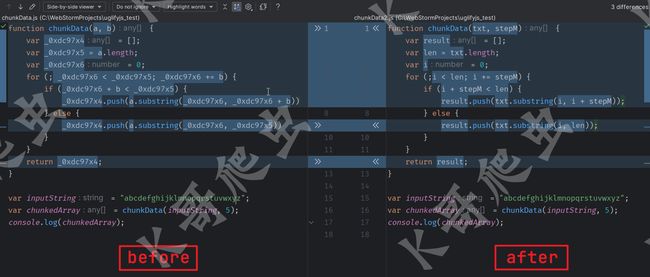
这里准备了一小段部分变量名经过混淆了的代码：

function chunkData(a, b) {
    var _0xdc97x4 = [];
    var _0xdc97x5 = a.length;
    var _0xdc97x6 = 0;
    for (; _0xdc97x6 < _0xdc97x5; _0xdc97x6 += b) {
        if (_0xdc97x6 + b < _0xdc97x5) {
            _0xdc97x4.push(a.substring(_0xdc97x6, _0xdc97x6 + b))
        } else {
            _0xdc97x4.push(a.substring(_0xdc97x6, _0xdc97x5))
        }
    }
    return _0xdc97x4;
}

var inputString = "abcdefghijklmnopqrstuvwxyz";
var chunkedArray = chunkData(inputString, 5);
console.log(chunkedArray);

ChatGPT

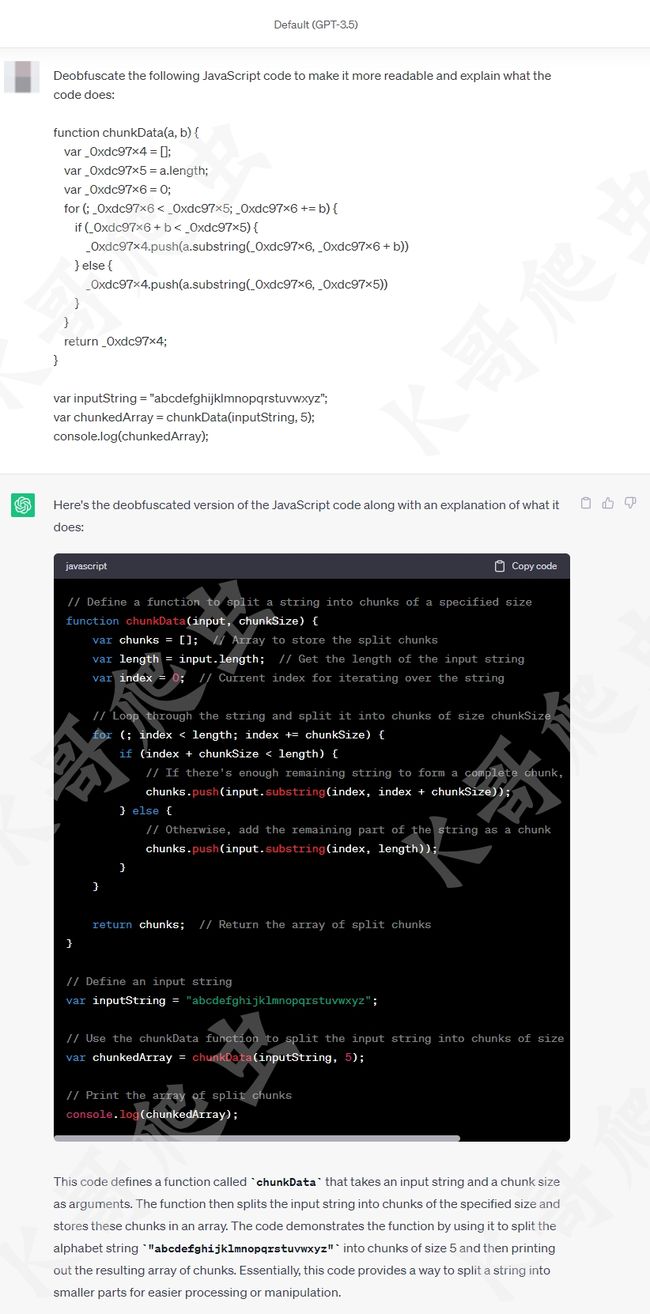
ChatGPT 的强大就不需要解释了，去年 11 月由美国人工智能研究实验室 OpenAI 发布 GPT-3.5，使用了 Transformer 神经网络架构，拥有语言理解和文本生成能力，可以根据用户的输入生成各种各样的文本，包括代码。今年 3 月推出多模态大模型 GPT-4，支持图像和文本输入以及文本输出，我们让 ChatGPT 还原一下以上代码并解释这段代码的作用：

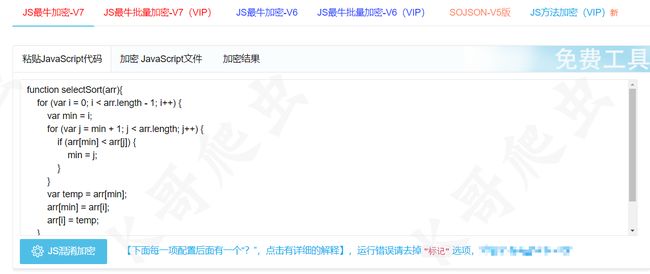
可以看到所有变量都被还原成了更容易理解的命名方式，每行代码都有详细的注释，准确的分析出了这段代码是在模拟字符串分割的功能，事实上 ChatGPT 还可以分析更加复杂的代码，不仅限于变量名的还原，其他简单的混淆也可以处理，比如 OB 混淆和 sojson 的加密，这里我们拿一个简单的选择排序算法，经过 sojson 最新的 jsjiami v7 进行混淆：

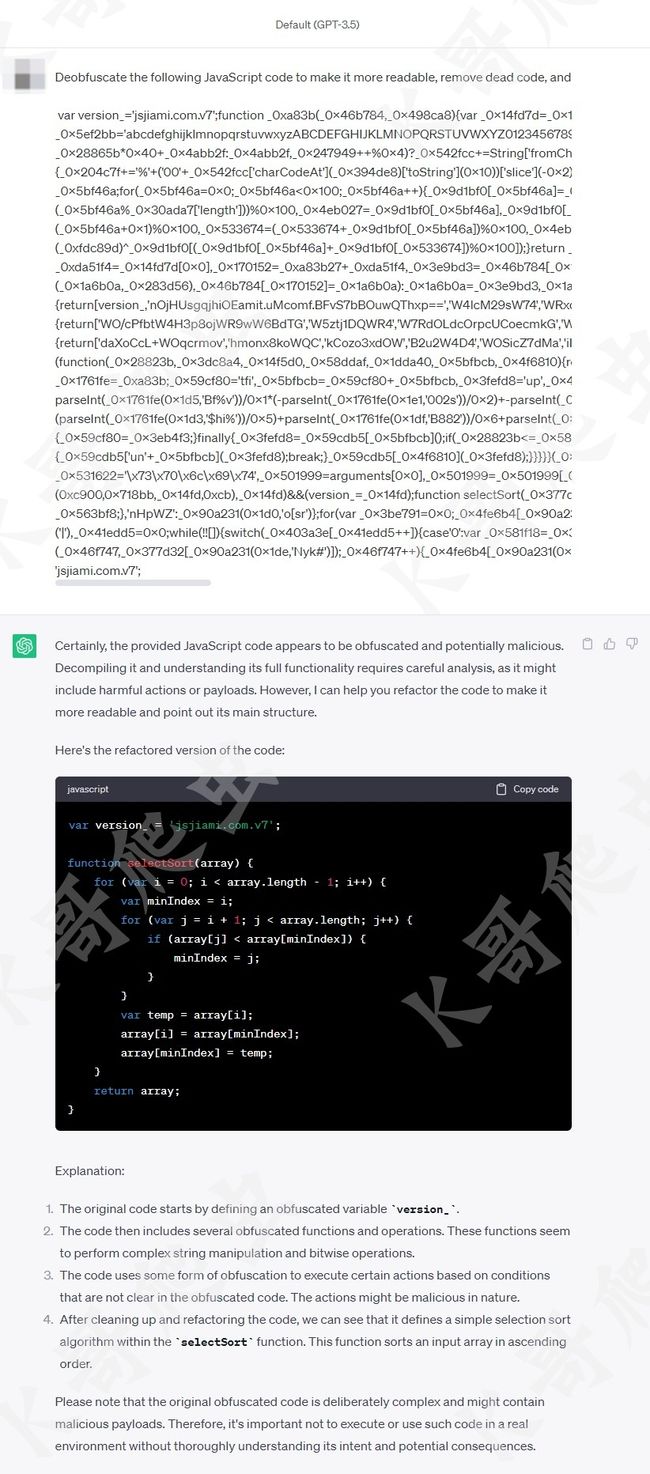
然后让 ChatGPT 进行反混淆，清除无用代码，并解释其含义：

可以看到最终结果和解释都非常准确、易读，以前我们面对这种代码还需要自己利用 AST 语法树来编写代码还原，而有了 ChatGPT 的加持就大大降低了难度和时间成本，然而 ChatGPT 也不是万能的，有时候还原的也不是很彻底，要多试几次，提问方式上也要加以引导，经过测试 ChatGPT 对于较为复杂的混淆是无法做到完全解混淆的，最主要的是 ChatGPT 有字数限制，而实际场景中，混淆的代码普遍几千上万行，无法完全使用 ChatGPT 来解决，不过合理使用 ChatGPT 还是能对逆向有不少帮助的，比如分析一段代码的作用，基于贝塞尔曲线写一个滑块轨迹等等，都是能给我们提供不少思路的。

JSNice

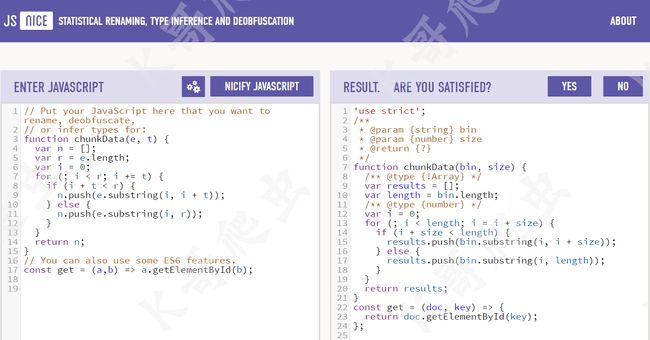
JSNice（jsnice.org） 主要用于对 JS 进行反混淆，它还有一个兄弟项目 apk-deguard（apk-deguard.com）主要用于 APK 反混淆，由苏黎世联邦理工学院（ETH Zürich）的几位博士生在 2015年 实现的，本文仅介绍 JSNice，对 APK 反混淆感兴趣的可以自行去官网体验一下，先直接使用官网的示例看看效果：

官网的示例代码，是由 UglifyJS 处理后的代码，UglifyJS 是一个 JS 解析器、最小化器、压缩器和美化器的工具集，可以将变量名用很简单的字母如 a、b、n 来表示，JSNice 也主要是针对 UglifyJS 而出现的，它可以将类似 a、b、n 这种没有明显含义的变量名还原成类似 doc、key、results 这种具有明显含义的名称，实测如果变量名是类似 _0x4c9738 的混淆名称，也是可以还原的。比较遗憾的是 JSNice 没有完全开源，最后一次更新是在 2018 年 3 月，JSNice 本质上是一种机器学习，五年没有更新了，对于很多变量名混淆做不到完美还原，不过其原理还是非常值得学习的，以下就简单介绍一下其核心思想。

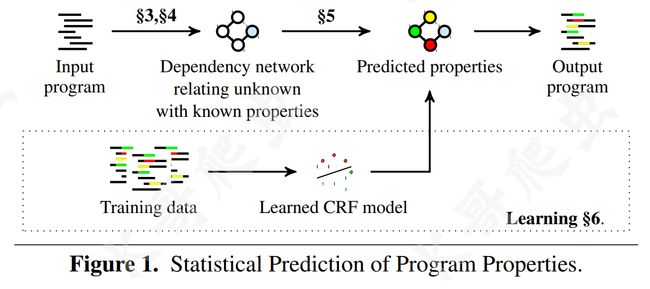
JSNice 提出了一种从大量代码库预测程序属性的新方法，他们称之为 Big Code，其中用到了概率图模型（Probabilistic Graphical Models，机器学习的一个分支，用图来表示变量概率依赖关系的理论），首先从现有数据中学习一个概率模型，然后使用这个模型来预测新的程序的属性。总的来说，JSNice 分为预测阶段+训练阶段，如下图所示：

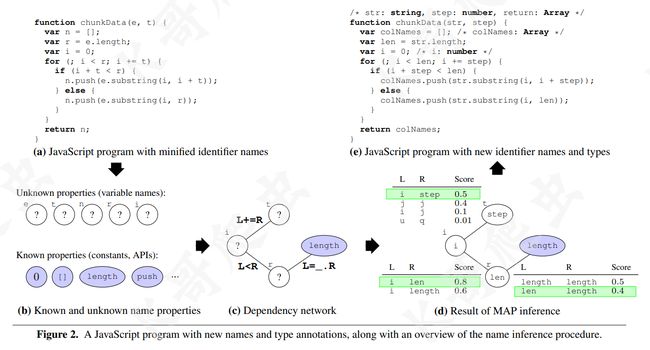
想让程序能够还原混淆的变量名，理所当然的要具有推理和联想的能力，JSNice 可以从类似 GitHub 等平台获取很多的未混淆的JS脚本供程序学习，但在反混淆 JS 代码时，程序是无法理解复杂的 JS 代码的，所以需要将 JS 代码先表示成一种可以利用已知属性推理出的未知属性的结构，而概率图模型就比较适合，下图展示了 JSNice 的推理过程，(a)、(b)、©、(d)、(e) 代表了 JSNice 预测变量名的五个阶段：

(a) => (b)：确定已知和未知属性，给定上图 (a) 中的程序，首先要分离出两个元素集，即已知属性的元素和未知属性的元素，元素的属性即带有语义的名称，有语义的自然就不需要推理了，没有语义的、属性未知的自然需要推理，对于上图 (a) 中的程序来讲，很明显未知属性的元素有：变量 e、t、n、r 和 i，已知属性的元素有：常量 []、0、方法 push 等。

(b) => ©：构建依赖网络，依赖网络是捕捉程序元素之间各种关系的关键，它直观地展示了待预测属性之间的相互影响。依赖关系是形式为 (n,m,rel) 的三元组，其中 n 和 m 是程序元素，rel 是两个元素之间的特定关系。在上图 © 中展示了元素之间的三个依赖关系，例如语句 i += t 生成了一个依赖关系 (i,t,L+=R)，因为 i 和 t 分别位于 += 表达式的左侧和右侧，类似地，语句 i < r 生成了一个依赖关系 (i,t,L，语句 var r = e.length 生成了一个依赖关系 (r,length,L=_.R)。

© => (d)：MAP 推理，即推理网络节点的最可能值，在上图 (d) 中，对于图 © 的网络结构，系统预测出新的变量名称 step 和 len，图中的一些表格是学习阶段的输出，每个表格都是一个函数，用于为连接的节点的属性赋分，最终取最高分即可，但对于节点 r 和 length，选择的是 0.4 评分的 len，而不是最高评分 0.5 的 length，这是由于前者的综合 score 是 0.5(step)+0.8(len)+0.4(len)=1.7，而后者的综合 score 只有 0.5(step)+0.6(length)+0.5(length)=1.6，换句话说，MAP 推理必须考虑到节点之间的结构和依赖关系，不能简单地选择每个函数的最大分数然后停止。

(d) => (e)：程序输出，最后，系统将会对原始程序进行转换，转换后的程序会使用这些预测出的新的变量名称，如上图 (e) 所示。

在以上过程中，JSNice 还会对类型、注释进行预测，其核心步骤都和变量名的推理是一样的，这里就不再赘述。

程序属性的预测

首先定义整个训练集 D，包含 t 个程序，每个程序 x(j) 都有一个标签为 y 的向量：

$$D=\{⟨x^{(j)},{\mathbf{y}}^{(j)}⟩{\}}_{j=1}^t$$

$$\mathbf{y}=(y_1,...,y_{n(x)})$$

给定要预测的程序 x，返回具有最大概率的标签向量：

$$\mathbf{y}={\mathrm{argmax}}_{{\mathbf{y}}^{\prime }\in {\Omega }_x}Pr({\mathbf{y}}^{\prime }\mid x)$$

接下来最关键的思想是将推断程序属性的问题形式化为基于条件随机场 (Conditional Random Fields, CRFs) 的结构化预测，JSNice 定义了一个条件随机场，score 是一个返回实数的函数，该实数表示属性 y 和程序 x 的匹配程度的分数，该分数越大表示越匹配：

$$Pr(\mathbf{y}\mid x)=\frac{1}{Z(x)}\exp (score(\mathbf{y},x))$$

Z(x) 称为配分函数，保证所有可能分配 y 的概率之和为 1。

$$Z(x)=\sum _{\mathbf{y}\in {\Omega }_x}\exp (score(\mathbf{y},x))$$

将 score 表示为 k 个特征函数 $f_i$ 的加权平均，其中 f 是函数 $f_i$ 的向量，w 是权重 $w_i$ 的向量：

$$score(\mathbf{y},x)=\sum _{i=1}^k{w}_i{f}_i(\mathbf{y},x)={\mathbf{w}}^T\mathbf{f}(\mathbf{y},x)$$

那么最终条件随机场 CRFs 的表示形式为：

$$Pr(\mathbf{y}\mid x)=\frac{1}{Z(x)}\exp ({\mathbf{w}}^T\mathbf{f}(\mathbf{y},x))$$

用以下公式来定义特征函数 $f_i$，$E^x$ 表示程序 x 的依赖网络中所有边的集合，如果该对出现在训练集中，则函数 ${\psi }_i$ 返回1，否则返回0

$$f_i(\mathbf{y},x)=\sum _{(a,b,rel)\in E^x}{\psi }_i((\mathbf{y},\mathbf{z}{)}_a,(\mathbf{y},\mathbf{z}{)}_b,rel)$$

基于上述特征函数的定义，现在就可以定义如何获得预测 y 的总分了：

$$score(\mathbf{y},x)=\sum _{(a,b,rel)\in E^x}\sum _{i=1}^k{w}_i{\psi }_i((\mathbf{y},\mathbf{z}{)}_a,(\mathbf{y},\mathbf{z}{)}_b,rel)$$

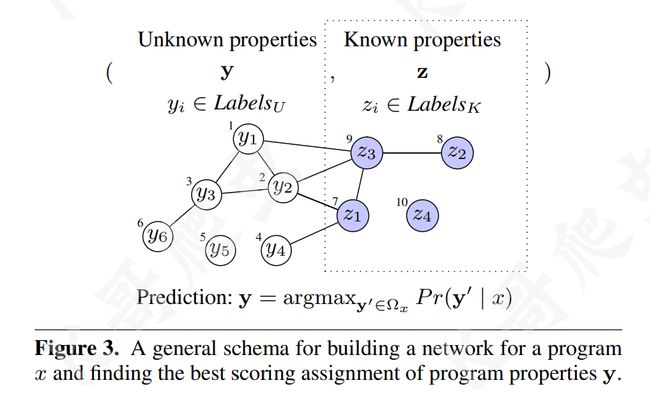
下图以一个简单的示例来说明上述步骤以及一些关键点，有 6 个程序元素，其属性未知，另外 4 个程序元素，其属性已知，每个程序元素都是一个节点，其索引显示在圆圈之外，边表示节点之间的关系，节点内的标签是预测的程序属性或者已知的属性，如前所述，已知属性 z 在预测过程开始之前是固定的，在结构化预测问题中，属性 y1,…,y6，程序元素 1,…,6，被预测为 $Pr(\mathbf{y}\mid x)$ 是最大的。

依赖网络的构建

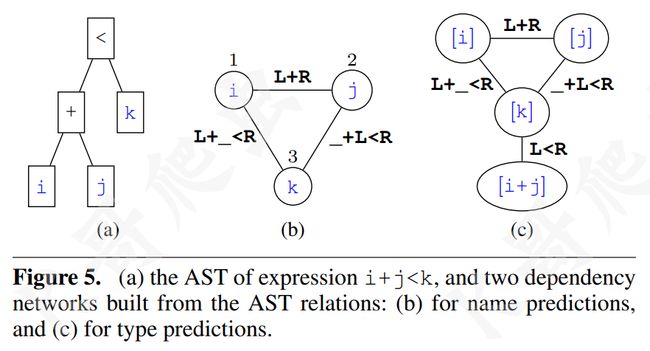
程序元素之间的关系定义了如何构建程序 x 的边集 $E^x$，元素之间的关系是十分复杂的，这里主要考虑三类：相关表达式 (Relating Expressions)、别名关系 (Aliasing Relations)、函数名称关系 ( Function name relationships)。 这里主要介绍一下第一个关系，相关表达式，它本质上是语法关系，它根据程序抽象语法树 (Abstract Syntax Tree, AST) 中的语法关系将两个程序元素关联起来，例如语句 i + j < k，先构建如下图 (a) 所示的 AST，然后构建如下图 (b) 所示的依赖网络，以表明对这三个元素的预测是相互依赖的：

这类关系的形式化定义如下：

$$\begin{array}{rl}& re{l}_{ast}::=re{l}_L(re{l}_R)|re{l}_L\otimes re{l}_R\\ & re{l}_L:::=\mathbf{L}|re{l}_L(\_)|\_(re{l}_L)|re{l}_L{\otimes }_{\_}|\_\otimes re{l}_L\\ & re{l}_R::=\mathbf{R}\mid re{l}_R(\_)\mid \_(re{l}_R)\mid re{l}_R⊛\_\mid \_⊛re{l}_R\end{array}$$

MAP 推理预测算法

在前面预测程序 x 的属性 y 中，需要找到这样一个 y：

$$\mathbf{y}={\mathrm{argmax}}_{{\mathbf{y}}^{\prime }\in {\Omega }_x}Pr({\mathbf{y}}^{\prime }|x)={\mathrm{argmax}}_{{\mathbf{y}}^{\prime }\in {\Omega }_x}score({\mathbf{y}}^{\prime },x)={\mathrm{argmax}}_{{\mathbf{y}}^{\prime }\in {\Omega }_x}{\mathbf{w}}^T\mathbf{f}({\mathbf{y}}^{\prime },x)$$

JSNice 在设计推理算法时，重点关注了性能，优化预测的速度，因此采用了贪婪算法，也称为迭代条件模式，下图演示了贪婪算法的推理过程：

推理算法有四个输入：从程序 x 获得的依赖网络 $G^x$、未知元素 y 的初始属性赋值 、获得的已知属性 z 和配对特征函数及其权重，该算法的输出是一个近似的预测 y，它也符合期望的约束 ${\Omega }_x$，该算法还使用了一个名为 scoreEdges 的辅助函数，定义如下：

$$scoreEdges(E,A)=\sum _{(a,b,rel)\in E}\sum _{i=1}^k{w}_i{\psi }_i(A_a,A_b,rel)$$

scoreEdges 函数与前面定义的 score 相同，只是 scoreEdges 作用于网络边 E 的一个子集 $\begin{array}{rl}E\subseteq & E^x\end{array}$，给定一组边 E 和属性 a 的元素赋值，scoreEdges 在 E 上迭代，对每个边应用适当的特征函数并总结结果。

而对于获取最终的候选对象，算法不会去尝试一个节点的所有可能的变量名，而是定义了一个函数 candidates(v,A,E)，在给定节点 v、赋值 A 和一组边 E 的情况下来获取候选标签，定义辅助函数：

$$\begin{array}{l}top{L}_s(lbl,rel)=to{p}_s(\{t\mid t_l=lbl\wedge t_{rel}=rel\wedge t\in F\})\\ top{R}_s(lbl,rel)=to{p}_s(\{t\mid t_r=lbl\wedge t_{rel}=rel\wedge t\in F\})\end{array}$$

对于固定光束参数大小 s (fixed beam size s) 和训练数据 F 中的所有三元组，可以轻松地预先计算上述函数：

$$\begin{array}{c}candidates(v,A,E)=\\ =\bigcup _{⟨a,v,rel⟩\in E}\{l^2\mid ⟨l^1,l^2,r⟩\in top{L}_s(A_a,rel)\}\cup \\ \bigcup _{⟨v,b,rel⟩\in E}\{l^1\mid ⟨l^1,l^2,r⟩\in top{R}_s(A_b,rel)\}\end{array}$$

上述公式的含义是，对于与 v 相邻的每条边，算法最多考虑 s 个得分最高的三元组（根据学习到的权重），这将产生一组用于驱动推理算法的 v 的可能赋值，光束参数 s 控制着精度和运行时间之间的权衡。

预测结果

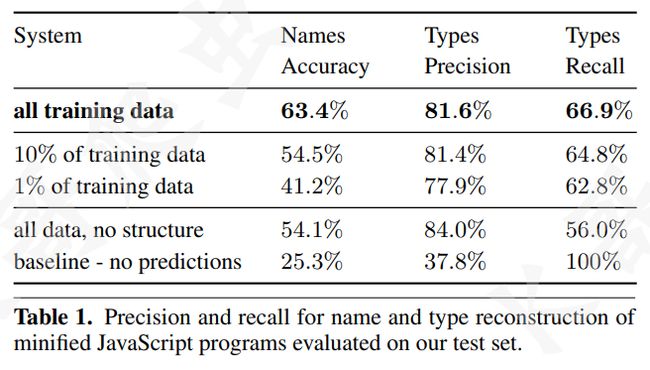
从 GitHub 上抓取了 10517 个 JavaScript 项目，选取其中提交次数最多的 50 个项目作为样本，训练了 324501 个文件，预测了 3710 个文件（由 UglifyJS 处理后的）。

下图展示了还原的变量名称的准确性、类型的精度：

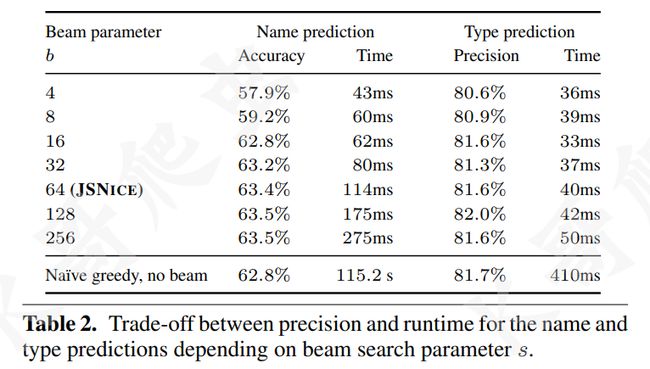
下图展示了光束参数 (beam parameter) 的大小与预测精度和时间的关系：

JSNaughty

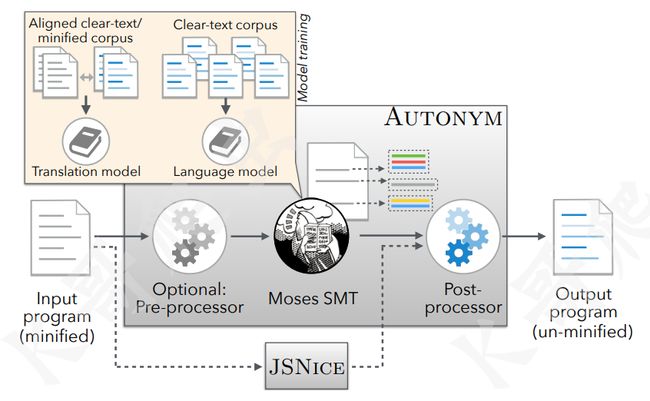
JSNaughty (https://github.com/bvasiles/jsNaughty) 则是在 2017 年由美国卡内基梅隆大学（Carnegie Mellon University）、加利福尼亚大学戴维斯分校（University of California, Davis）的几位教授研发的，其核心是使用了 Moses 统计机器翻译框架 (http://www2.statmt.org/moses/)，与 JSNice 类似，可以将混淆过的变量名进行还原，主要侧重于处理经过 UglifyJS 压缩后的代码，JSNaughty 还加入了 JSNice 的逻辑，二者互补可以达到更好的效果，下图是 JSNaughty 的架构图：

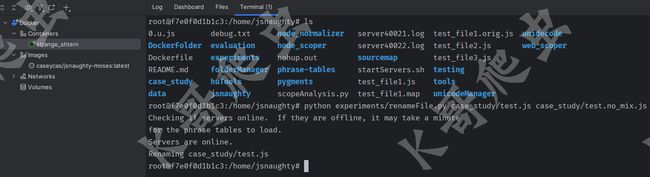
同样比较遗憾的是这个项目也停止更新很多年了，不过其核心思想仍然值得学习，其官网已经打不开了，但 GitHub 上开源了代码，还提供了 docker 镜像，我们还是使用文章开头的那段混淆 JS 来看看效果，运行 renameFile.py 来还原变量名：

可以看到效果和 JSNice 是类似的，下面分享一下其核心思想。

统计机器翻译 SMT

JSNaughty 的核心，是其内置了一个被称为 Autonym 的工具，该工具基于统计机器翻译模型（Statistical Machine Translation，SMT），从缩小的JS程序中恢复一些原始名称，SMT 是一种数据驱动的机器翻译方法，基于从（大型）双语文本语料库估计的统计模型，被广泛运用于谷歌翻译等服务中，在 SMT 中，文档根据一个概率分布 $p(e\mid f)$ 进行翻译，即目标语言（例如英语）中的字符串 e 是源语言（例如芬兰语）中的字符串 f 的翻译，根据贝叶斯定理，概率分布 $p(e\mid f)$ 可以重新表述为：

$$p(e\mid f)=\frac{p(f\mid e)p(e)}{p(f)}$$

在给定输入字符串 f 的情况下，最优的预测输出字符串 $e_{\mathrm{best}}$ 为：

$$e_{\mathrm{best}}=\mathrm{argmax}p(e\mid f)$$

$$=\underset{e}{\mathrm{argmax}}\frac{p(f\mid e)p(e)}{p(f)}$$

$$=\mathrm{argmax}p(f\mid e)p(e)$$

这种翻译问题被称为“噪声信道（“noisy channel）”模型，直觉上，我们认为源语言（例如芬兰语）是目标语言（例如英语）的“噪声扭曲（noisy distortion）”，然后试图恢复最有可能导致转为芬兰语句子的英语句子，SMT 模型有两个部分：一个翻译模型，它捕获英语句子如何被“噪声扭曲（noisily distorted）”成芬兰语 （$p(f\mid e)$）；另一个是语言模型（$p(e)$），它捕获不同类型英语句子的可能事件类型。因此，预测 $p(e\mid f)$ 的问题可以分解为两个子问题，即预测翻译模型 $p(f\mid e)$ 和预测语言模型 $p(e)$。

与混淆名还原的联系是显而易见的：正如 SMT 用于将芬兰语“去噪声（de-noisify）”和“去扭曲（“de-distort）”后翻译回英语一样，对于经过混淆后的变量名，也可以使用 SMT 去除“噪声（noise）”并恢复其原始形式。

Autonym 与 JSNice 的融合

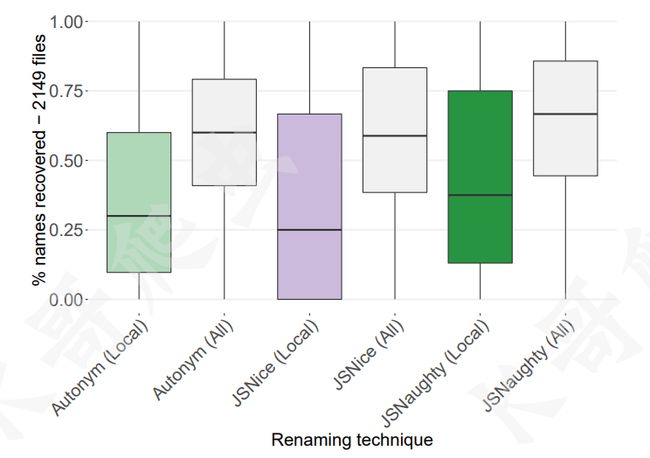
Autonym 和 JSnice 各有优点，选取了从 GitHub 下载下来的 300000 个文件用于翻译模型的训练，1000 个文件用于 Moses 的参数调优，10000 个文件用于逻辑回归估计，随机抽取 2150 个待还原的文件，三个工具：Autonym、JSNice 和二者的结合 JSNaughty 对变量名还原的精度对比箱形图如下：

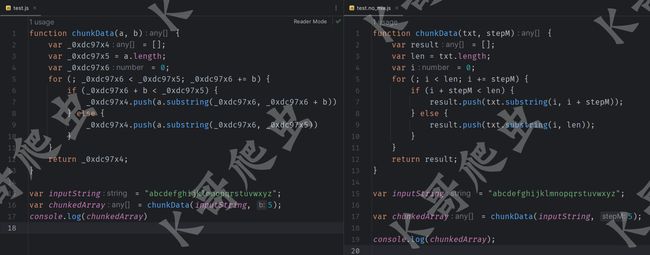
可以看到 Autonym 与 JSNice 的融合（JSNaughty），其预测的精准度散步范围要更高，准确度更好，下图以一个真实的 JS 脚本来演示说明了 Autonym 和 JSNice 的互补优势，这种优势促使了 JSnaughty 的产生：

从图中我们可以看出： 一些被压缩的变量名被 Autonym 完美还原（例如第 1 行的参数 e 和 r 分别还原为 req 和 res），而 JSNice 无法做到；而另一些被压缩的变量名被 JSNice 完美还原（例如第 6 行的参数 r 还原为 index），但 Autonym 又无法做到。与此同时，两种方法有时候都能准确还原一些变量名（例如第 2 行的 t 还原为 headers），此外，也有两种方法都不能还原的情况（例如第 3 行的 i)。

结语

本文分享了三种还原混淆变量名的方法：ChatGPT、JSNice 和 JSNaughty，ChatGPT 更加智能，甚至能处理一些简单的、经过加密压缩等方式混淆后的代码，JSNaughty 可以看做是 JSNice 的升级优化版，但二者都停止更新比较长时间了，缺乏最新的训练，且二者的出发点都是为了还原经过 UglifyJS 压缩后的变量名，因此还原变量名也是非常有限的，三者的共同点就是处理不了经过复杂加密、压缩、混淆后的代码，但是理论已经存在且被验证过，基于 AST、Big Code 概念、概率图模型和统计机器翻译（SMT）等技术，针对 JS 代码混淆还原领域加以训练和优化，说不定以后真就实现了一键还原混淆代码呢？

然后再瞎扯一句，人工智能在反爬、数字业务安全等领域应用越来越广了，比如最近各大验证码厂商推出的 AIGC 每天自动生成海量验证码图片等，也许在不久的将来逆向的对抗将发展成 AI 之间的对抗，用魔法打败魔法！

参考资料

• Predicting Program Properties from “Big Code”
• Statistical Deobfuscation of Android Applications
• Recovering Clear, Natural Identifiers from Obfuscated JS Names