数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成

数据生成 | MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成

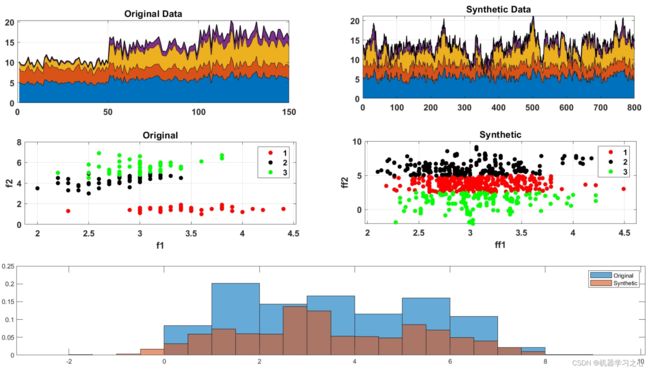
生成效果

基本描述

1.MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成；
2.马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo)，简称MCMC，MCMC算法的核心思想是我们已知一个概率密度函数，需要从这个概率分布中采样，来分析这个分布的一些统计特性。

模型描述

马尔科夫蒙特卡洛模拟（Markov Monte Carlo simulation）是一种基于马尔科夫链的随机模拟方法，用于生成服从某个特定分布的数据样本。下面是使用马尔科夫蒙特卡洛模拟生成数据的一般过程：
定义状态空间：确定数据的可能取值范围，可以是一个离散的状态空间或者一个连续的状态空间。
构建转移矩阵：根据问题的特点，确定状态之间的转移概率。转移矩阵描述了从一个状态转移到另一个状态的概率。
初始化状态：从状态空间中选择一个初始状态。
进行模拟：根据转移矩阵和当前状态，按照一定的概率规则转移到下一个状态。重复这个过程多次，直到达到所需的样本数量。
生成样本：记录每个状态的取值，得到生成的数据样本。

程序设计

• 完整程序和数据获取方式：私信博主回复MATLAB实现MCMC马尔科夫蒙特卡洛模拟的数据生成。

tempLayers = [
    convolution2dLayer([3, 1], 16, "Name", "conv_1", "Padding", "same")  % 建立卷积层,卷积核大小[3, 1]，16个特征图
    reluLayer("Name", "relu_1")                                          % Relu 激活层
    convolution2dLayer([3, 1], 32, "Name", "conv_2", "Padding", "same")  % 建立卷积层,卷积核大小[3, 1]，32个特征图
    reluLayer("Name", "relu_2")];                                        % Relu 激活层
lgraph = addLayers(lgraph, tempLayers);                                  % 将上述网络结构加入空白结构中

tempLayers = [
    sequenceUnfoldingLayer("Name", "sequnfold")                      % 建立序列反折叠层
    flattenLayer("Name", "flatten")                                  % 网络铺平层

lgraph = addLayers(lgraph, tempLayers);                              % 将上述网络结构加入空白结构中
lgraph = connectLayers(lgraph, "seqfold/out", "conv_1");             % 折叠层输出 连接 卷积层输入
lgraph = connectLayers(lgraph, "seqfold/miniBatchSize", "sequnfold/miniBatchSize"); 
                                                                     % 折叠层输出连接反折叠层输入
lgraph = connectLayers(lgraph, "relu_2", "sequnfold/in");            % 激活层输出 连接 反折叠层输入

%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法
    'MaxEpochs', 500,...                 % 最大训练次数 1000
    'InitialLearnRate', best_lr,...          % 初始学习率为0.001
    'L2Regularization', best_l2,...         % L2正则化参数
    'LearnRateSchedule', 'piecewise',...  % 学习率下降
    'LearnRateDropFactor', 0.1,...        % 学习率下降因子 0.1
    'LearnRateDropPeriod', 400,...        % 经过800次训练后 学习率为 0.001*0.1
    'Shuffle', 'every-epoch',...          % 每次训练打乱数据集
    'ValidationPatience', Inf,...         % 关闭验证
    'Plots', 'training-progress',...      % 画出曲线
    'Verbose', false);

%% 训练
net = trainNetwork(p_train, t_train, lgraph, options);

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229