机器学习——线性回归衍生(过拟合、正则化、岭回归和LASSO回归)
过拟合、正则化、岭回归、LASSO回归
- 为什么会出现线性回归的衍生方法——正规方程法的局限
- 过拟合
-
- 模型复杂度
- 过拟合的概念
- 防止过拟合的办法
- 正则化
- 岭回归(Ridge Regression)
-
- 1. Ridge回归基本思想
- 2. 求解岭回归——正规方程法
- 3. 岭系数
- 4. 岭回归的特点
- LASSO回归(Least absolute shrinkage and selection operator)
-
- 1. LASSO回归基本思想
- 2. LASSO回归的特点
- 3. 岭迹图
- 写在最后
ps.之前啃ESL这本书的时候,接触到这块内容,希望能结合自己的理解,把线性回归正则化的内容解释清楚。从为什么出现线性回归的衍生方法?(最小二乘(正规方程法)解决不了)到传统方法解决不了的情况会带来什么问题?(过拟合)再到如何处理这种问题?(正则化)最后介绍正则化的几种方法。(岭回归和LASSO)
为什么会出现线性回归的衍生方法——正规方程法的局限
tips.正规方程法的局限或者叫最小二乘法的局限(在ESL中)希望小伙伴们不要对这两个词有什么误解,正规方程就是将最小二乘的线性方程组拓展到矩阵的一种解法。
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程(或称为法方程)。
——百度百科
上篇博文的最后介绍了求解线性回归的正规方程法(☞详情请戳☜)。通过矩阵运算,求解得到系数的估计: θ ^ = ( X T X ) − 1 X T Y \hat\theta=(X^TX)^{-1}X^TY θ^=(XTX)−1XTY其中, ( X T X ) − 1 (X^TX)^{-1} (XTX)−1是 X T X X^TX XTX的逆矩阵。
由此,我们可以得到一个限制条件: X T X X^TX XTX必须可逆。但是在如下情况时矩阵 X T X X^TX XTX不可逆:
1.存在线性相关的特征—多重共线性 。
例如:一个电信数据集中,存在变量:白天通话时长(Day_Mins)、白天通话话费(Day_Charge),显而易见,通话时长越久,话费自然越高。通过做相关图,两个变量存在严重的正相关。
2.特征数据太多(样本数m < 特征数n)
PS.ESL中通过解释力Interpretation 和预测精度Prediction accuracy两个角度解释最小二乘法的局限:
There are two reasons why we are often not satisfied with the least squares estimates (3.6).
• The first is prediction accuracy: the least squares estimates often have low bias but large variance.Prediction accuracy can sometimes be improved by shrinking or setting some coefficients to zero. By doing so we sacrifice a little bit of bias to reducethe variance of the predicted values, and hence may improve the overall prediction accuracy.
• The second reason is interpretation. With a large number of predictors, we often would like to determine a smaller subset that exhibit the strongest effects. Inorder to get the “big picture” ,we are willing to sacrifice some of the small details.
简译过来为:
| Prediction accuracy(预测精度) | Interpretation(解释力) |
|---|---|
| 当n(观测数量)、p(特征数)很接近时,模型拟合效果差。为了提高泛化能力,常常表现出低偏倚,高方差的特点。 | 预测变量较多时,造成:①模型复杂度增加②多重共线性。 |
上述两种情况都是因为特征问题而导致最小二乘无法求解线性回归,这时针对特征的处理办法有:
- 子集选择
- 降维
- 特征收缩——正则化
子集选择和降维比较容易理解,在这里,我们主要梳理正则化的概念。
那正则化是做什么呢?首先我们要说一说过拟合的概念。
过拟合
模型复杂度
在上述特征数较多的场景,不可避免的会带来模型复杂度增大的情形,我们针对特征的处理方法也是在降低模型复杂度。模型复杂度体现在哪些方面呢?比如说:
在我们拟合模型时,由于我们希望得到更好的泛化误差,容易对训练集拟合过于彻底,这时系数较多,可能有很多系数很大,模型较复杂。这时,训练数据一点儿变动会导致预测结果产生很大变动,模型泛化能力会很弱。
- 例1(从interpretation上降低模型复杂度):若一个因变量Y,其影响因素X有1000个: x 1 , x 2 , x 3 , . . . , x 1000 x_1,x_2,x_3,...,x_{1000} x1,x2,x3,...,x1000,若通过学习之后只剩下10个变量,那么就认为这10个因素所提供的信息量起决定性作用,就可以只分析这10个变量: Y = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β 10 x 10 + ϵ Y=\beta_0+\beta_1x_1+\beta_2x_2+⋯+\beta_{10}x_{10}+\epsilon Y=β0+β1x1+β2x2+⋯+β10x10+ϵ模型整体可解释性更强。
- 例2(从减少参数上降低模型复杂度)同样是Endrew Ng的房价例子

上图是从简单的参数较少的模型到复杂的参数较多模型的函数曲线变化图。
在这个时候就该“奥卡姆”出场了~~
奥卡姆剃刀原理:在所有可能的模型中,我们应该选择能够
很好地解释已知数据,并且十分简单的模型。
综上,模型复杂度越高就会导致模型泛化能力越弱。
通过R做图如下:(其中红色曲线是测试误差;蓝色曲线是训练误差。)
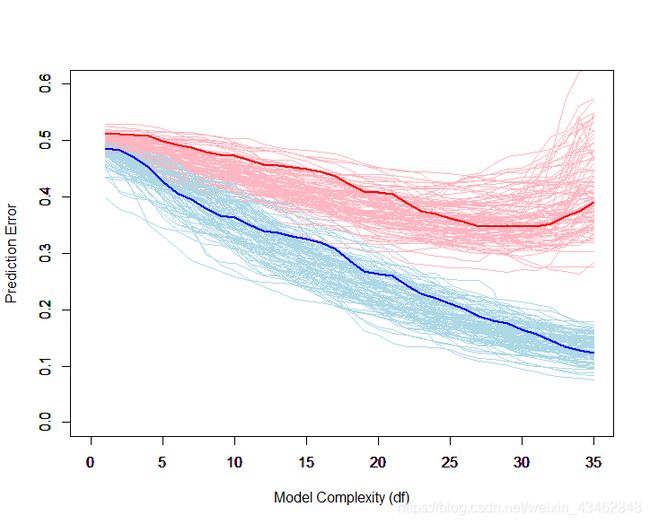
若有需要代码的小伙伴,请戳☞传送门☜
过拟合的概念
说了这么多,其实过拟合就是模型在训练数据上拟合的过于彻底,从而导致学习了较多训练数据独有的特征,使得模型在新的测试数据上表现较差。
我们举一个不太恰当的例子:我们想要根据一些特征来判断一个人是男是女,由于我们训练数据中的“发长”这个特征男生都是短发、女生大多是长发,这时我们的测试集中存在的长发男生就可能被错判成女生。
防止过拟合的办法
- 减少特征数:减少一些维度,降低复杂度。
- 增加数据量:数据量越大模型拟合越好。
- 正则化(Regularized):增加限制项缩减所有参数。
正则化
正则化就是通过增加一些限制项来缩减系数,达到降低模型复杂度的目的。
上篇博客,我们引入损失函数求解回归系数,使损失函数最小化,现在,要选取使损失函数最小化的最小的模型复杂度。而此时需要正则化项来达到控制模型复杂度的目的: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∗ L ( θ j ) J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda*L(\theta_j) J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λ∗L(θj)其中, λ \lambda λ是正则化参数, L ( θ j ) L(\theta_j) L(θj)为正则化项。我们最终的目的是使带罚项的损失函数达到最小,用一个例子来看——

通过 m i n J ( θ ) minJ(\theta) minJ(θ)来简化函数为了使上式尽可能的小,可以想象,若我们加了一个较大的?,这时要使 J ( θ ) J(\theta) J(θ)最小化,最好的办法就是使 β 3 \beta_3 β3 、 β 4 \beta_4 β4趋向于0,得到右图简单模型。
λ的目标就是在损失函数最小化和参数最小化之间权衡。
接下来要介绍的岭回归和LASSO回归就是针对正则化项的不同表现形式。
岭回归(Ridge Regression)
1. Ridge回归基本思想
在回归系数平方和小于一个常数的约束下,使残差平方和最小化,从而限制回归系数的大小。 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2 θ ^ R i d g e = a r g m i n { ∑ i = 1 m ( θ 0 + θ 1 x ( 1 ) + θ 2 x ( 2 ) + . . . θ m x ( m ) − y ( i ) ) 2 , s . t . ∑ j = 1 n θ j 2 ≤ t \hat\theta^{Ridge}=argmin\lbrace {}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(1)}+\theta_2x^{(2)}+...\theta_mx^{(m)}-y^{(i)})^2,s.t.\sum_{j=1}^{n}\theta_j^2\leq t θ^Ridge=argmin{i=1∑m(θ0+θ1x(1)+θ2x(2)+...θmx(m)−y(i))2,s.t.j=1∑nθj2≤t
2. 求解岭回归——正规方程法
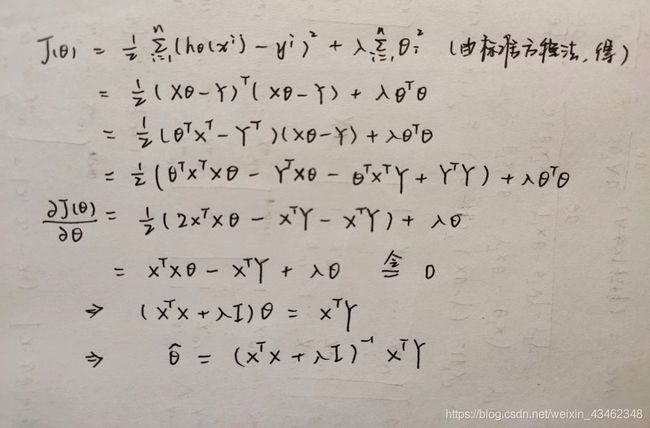
由上推导可得,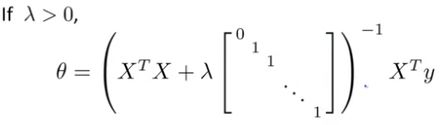
由于 X T X X^TX XTX对角线增加了 λ \lambda λ看起来像一条山岭,正是其岭回归的由来。
3. 岭系数

λ \lambda λ为岭系数, λ \lambda λ越小,参数数变化幅度越大。因为我们刚才说过 λ \lambda λ代表对参数的惩罚(压缩)程度,较大的 λ \lambda λ会对系数惩罚越大。
4. 岭回归的特点
参数逐步减小,但不会缩减到0
LASSO回归(Least absolute shrinkage and selection operator)
1. LASSO回归基本思想
在回归系数绝对值之和小于一个常数的约束下,使残差平方和最小化。
通过构造一个一阶惩罚函数获得一个精炼的模型,最终确定一些指标(变量)的系数为零(岭回归估计系数等于 0 的机会微乎其微,造成筛选变量困难)
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n ∣ θ j ∣ J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}|\theta_j| J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+λj=1∑n∣θj∣ θ ^ l a s s o = a r g m i n { ∑ i = 1 m ( θ 0 + θ 1 x ( 1 ) + θ 2 x ( 2 ) + . . . θ m x ( m ) − y ( i ) ) 2 , s . t . ∑ j = 1 n ∣ θ j ∣ ≤ t \hat\theta^{lasso}=argmin\lbrace {}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(1)}+\theta_2x^{(2)}+...\theta_mx^{(m)}-y^{(i)})^2,s.t.\sum_{j=1}^{n}|\theta_j|\leq t θ^lasso=argmin{i=1∑m(θ0+θ1x(1)+θ2x(2)+...θmx(m)−y(i))2,s.t.j=1∑n∣θj∣≤t
2. LASSO回归的特点
- 若LASSO和Ridge采用同样的梯度下降更新权值,得到结果为每次减少一个固定的值,从而能使某些系数缩减到0,得到解释性强的模型。
上图LASSO和岭回归的系数限制为:
L1正则化约束: ∣ β 1 ∣ + ∣ β 2 ∣ ≤ t |\beta_1|+|\beta_2|\leq t ∣β1∣+∣β2∣≤t
L2正则化约束: β 1 2 + β 2 2 ≤ t \beta_1^2+\beta_2^2\leq t β12+β22≤t
Lasso损失函数等值线与正则化约束交点——使其中一个系数为0,此时实现了特征选择。
Ridge既要满足损失函数尽可能小,又要满足约束条件,只能在切点处。因为若想让Ridge交在系数为0 处,需要使损失函数的等高线向外扩张,此时不满足损失函数最小条件。
3. 岭迹图

在ESL中,上面的岭迹图和刚才Ridge岭回归的不同,我一开始也是很懵,后来明白ESL岭迹图中横坐标为t(有没有很熟悉,是岭回归和lasso回归的约束值~),t越小,说明 λ \lambda λ对系数的惩罚越大,系数越会缩减到0。(如果还没有清楚,请拿出笔画一画,t减小,上图○和◇向原点移动, β 1 2 + β 2 2 \beta_1^2+\beta_2^2 β12+β22取值范围越小)
写在最后
本文主要介绍了一些线性回归的衍生方法,通过发现常规最小二乘解决不了的问题,找到其原因,对其进行优化,增加正则化项,使其变为线性回归可解决的问题。

