归一化的作用,sklearn 安装
目录
归一化的作用:
应用场景说明
sklearn
准备工作
sklearn 安装
sklearn 上手
线性回归实战
归一化的作用:
-
归一化后加快了梯度下降求最优解的速度;
-
归一化有可能提高精度(如KNN)
应用场景说明
1)概率模型不需要归一化,因为这种模型不关心变量的取值,而是关心变量的分布和变量之间的条件概率;
2)SVM、线性回归之类的最优化问题需要归一化,是否归一化主要在于是否关心变量取值;
3)神经网络需要标准化处理,一般变量的取值在-1到1之间,这样做是为了弱化某些变量的值较大而对模型产生影响。一般神经网络中的隐藏层采用tanh激活函数比sigmod激活函数要好些,因为tanh双曲正切函数的取值[-1,1]之间,均值为0.
4)在K近邻算法中,如果不对解释变量进行标准化,那么具有小数量级的解释变量的影响就会微乎其微。
sklearn
是集成了最常用的机器学习模型的 Python 库,使用起来非常轻松简单,有着广泛的应用。sklearn 全称 scikit-learn,其中scikit表示SciPy Toolkit,因为它依赖于SciPy库。learn则表示机器学习。
官网地址:https://scikit-learn.org/stable/
中文文档:https://www.sklearncn.cn/
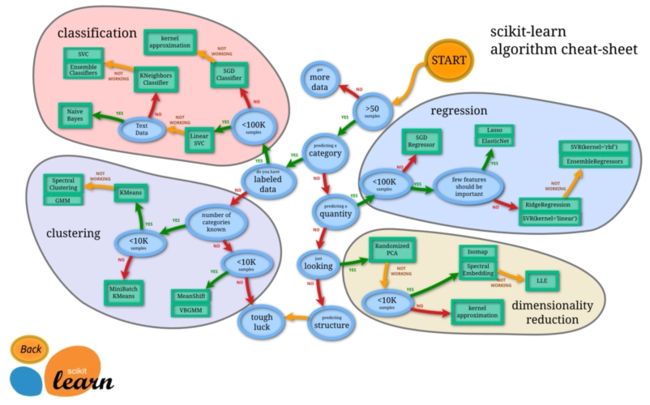
Scikit-learn的基本功能主要被分为六大部分:分类,回归,聚类,数据降维,模型选择和数据预处理。
1.分类:是指识别给定对象的所属类别,属于监督学习的范畴,最常见的应用场景包括垃圾邮件检测和图像识别等。
目前Scikit-learn已经实现的算法包括:支持向量机(SVM),最近邻,逻辑回归,随机森林,决策树以及多层感知器(MLP)神经网络等等。 需要指出的是,由于Scikit-learn本身不支持深度学习,也不支持GPU加速,因此这里对于MLP的实现并不适合于处理大规模问题。
2.回归:是指预测与给定对象相关联的连续值属性,最常见的应用场景包括预测药物反应和预测股票价格等。目前Scikit-learn已经实现的算法包括:支持向量回归(SVR),脊回归,Lasso回归,弹性网络(Elastic Net),最小角回归(LARS),贝叶斯回归,以及各种不同的鲁棒回归算法等。可以看到,这里实现的回归算法几乎涵盖了所有开发者的需求范围,而且更重要的是,Scikit-learn还针对每种算法都提供了简单明了的用例参考。
3.聚类:是指自动识别具有相似属性的给定对象,并将其分组为集合,属于无监督学习的范畴,最常见的应用场景包括顾客细分和试验结果分组。目前Scikit-learn已经实现的算法包括:K-均值聚类,谱聚类,均值偏移,分层聚类,DBSCAN聚类等。
4.数据降维:是指使用主成分分析(PCA)、非负矩阵分解(NMF)或特征选择等降维技术来减少要考虑的随机变量的个数,其主要应用场景包括可视化处理和效率提升。
5.模型选择:是指对于给定参数和模型的比较、验证和选择,其主要目的是通过参数调整来提升精度。目前Scikit-learn实现的模块包括:格点搜索,交叉验证和各种针对预测误差评估的度量函数。
6.数据预处理:是指数据的特征提取和归一化,是机器学习过程中的第一个也是最重要的一个环节。这里归一化是指将输入数据转换为具有零均值和单位权方差的新变量,但因为大多数时候都做不到精确等于零,因此会设置一个可接受的范围,一般都要求落在0-1之间。而特征提取是指将文本或图像数据转换为可用于机器学习的数字变量。需要特别注意的是,这里的特征提取与上文在数据降维中提到的特征选择非常不同。特征选择是指通过去除不变、协变或其他统计上不重要的特征量来改进机器学习的一种方法。
总结来说,Scikit-learn实现了一整套用于数据降维,模型选择,特征提取和归一化的完整算法/模块,虽然缺少按步骤操作的参考教程,但Scikit-learn针对每个算法和模块都提供了丰富的参考样例和详细的说明文档。
准备工作
任何一个工具箱都不是独立存在的,scikit-learn 是基于 Python 语言,建立在 NumPy ,SciPy 和 matplotlib 上。在上手sklearn之前,建议掌握的原理或工具有:
-
机器学习算法原理。
-
PyCharm IDE 或者 Jupyter Notebook。
-
Python的基本语法和Python中的面向对象的概念与操作。
-
Numpy的基本数据结构和操作方法(加减乘除、排序、查找、矩阵的计算等)。
-
Pandas读写数据的方法,举个例子,读csv文件中的数据,用Pandas也就一句data = pandas.read_csv('data.csv')。
-
Matplotlib 绘图工具,满足我们对基本的数据结果的各种展示需求。
sklearn 安装
scikit-learn 安装非常简单:
使用 pip
pip install -U scikit-learn
或者 conda:
conda install scikit-learn
如果你还没有Python和Anaconda或者PyCharm,可以参考这篇文章
sklearn 上手
学习sklearn最好的方式,就是在实践中学习,让我们来看看用sklearn实现线性回归的例子。线性回归的公式非常简单:
处于实际应用的角度,我们其实只关心两个问题:如何根据现有的数据算出线性回归模型的参数?参数求出之后我们怎么用它来预测?
sklearn 官网很直接地给出了这样一段代码:
import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
# y = 1 * x_0 + 2 * x_1 + 3
y = np.dot(X, np.array([1, 2])) + 3
reg = LinearRegression().fit(X, y)
reg.coef_
# array([1., 2.])
reg.intercept_
# 3.0000...
reg.predict(np.array([[3, 5]]))
# array([16.])
X
array([[1, 1],
[1, 2],
[2, 2],
[2, 3]])
y
array([ 6, 8, 9, 11])
这里注意下,X 是一个 5×2 的数组(和矩阵稍有不同,但形状完全一样),而y是一个一维的数组。由此可见,我们要用来拟合的数据,其输入变量必须是列向量,而输出的这个变量则相对自由(注意,这也是sklearn相对比较坑的一点;官方的说法是为了节省内存开销,但如果熟悉Matlab、R等相对更加专业的计算类程序的人容易觉得不适应)。
那么明白了这一点,我们要输入怎样的数据就完全明确了。那么如果我们想换上自己的数据不外乎也就是把 X 和 y 按照同样的格式输入即可。
-
第6行,首先是直接调用LinearRegression类的方法fit(X,y),直接实例化了一个线性回归模型,并且用上面生成的数据进行了拟合。
看到这里就能够明白了,原来只需要把数据按照格式输入,就可以完成模型的拟合。事实上这段代码也可以改成以下形式:
reg = LinearRegression()
reg.fit(X, y)
因为fit()方法返回值其实是模型本身self的一个实例(也就是返回了它自己,这个 LinearRegression对象),所以在初始化reg之后只需要直接调用fit(),它自己对应的系数值(属性)就被成功赋值。这种写法更为推荐,因为它虽然看起来多出一行,但整个运行的机制则显得更加清晰。
-
第9和11行是系数和偏差值的展示。上面提到,注释中已经说明了数据就是由方程 生成的,而这时我们看到系数值分别等于
1,2而偏差值是3,和理论模型完全一致。 -
第13行,此时它调用了
LinearRegression类的predict()方法。那么显然,这个方法就是利用拟合好的线性回归模型来计算新输入值对应的输出值。这里新输入值仍然和拟合时的格式保持一致。
那么小结一下,根据官方文档,要拟合一个线性回归模型并且预测出新值的话,其实只需要进行四个步骤:
-
格式化数据,输入为n*d的数组,其中n表示数据的个数,d是维度;输出值是一维数组
-
初始化模型LinearReregression()
-
拟合fit(X,y)
-
预测predict(X_test)
线性回归实战
实战案例中使用了diabetes数据集。该数据集包括442位糖尿病患者的生理数据及一年以后的病情发展情况。共442个样本,每个样本有十个特征,分别是 [‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’],对应年龄、性别、体质指数、平均血压、S1~S6一年后疾病级数指标。Targets为一年后患疾病的定量指标,值在25到346之间。
本节我们将通过糖尿病患者的体重bmi,预测糖尿病患者接下来病情发展的情况。在实际应用中,可以根据预测模型,提前预知患者的病情发展,从而提前做好应对措施,改善患者的病情。
# 导入必要的工具箱
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# 导入糖尿病数据集
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]# 取第三列bmi的值
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# fit()函数拟合
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients 输出回归系数
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction 决定系数,越接近1越好
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
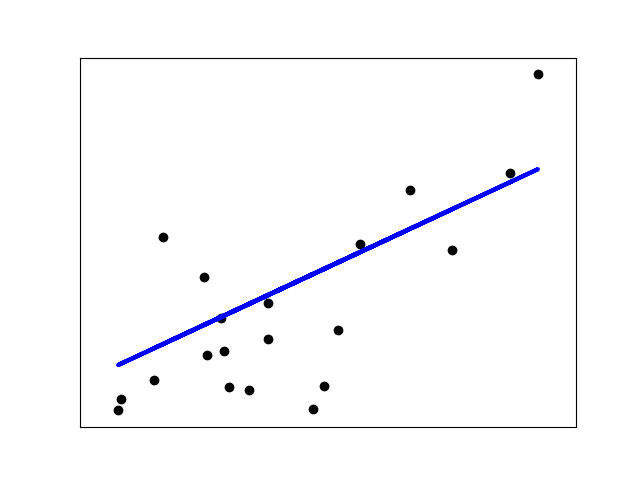
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
# print输出评价指标
Coefficients:
[938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47
通过模型可以看出,随着体重指标的增加,病情的级数也在增加,因此可以预测某位患者接下来一年内病情将会如何发展。当然,通过多变量分析我们可以得到更好的模型。