数据结构与算法7-递归、分治、回溯
目录
递归
递归必须满足的条件
递归的实现
递归的优化
不用递归
减少已执行次数
尾递归
数据结构前面六篇,我们整理了一些基本数据结构和一些算法的简单知识
今天,我们来接触一些算法相关的思想和它们的一些知识
递归
思考一下,B是A的孩子,C是B的孩子,请问C的最大长辈是谁?
这个很自然的,就能想到一层一层往上,C找B,B再找A,如果A还有,就继续往上
再思考一下,斐波那契数列 1 1 2 3 5 8 13 21
可以发现,前两个数相加,等于下一个数,这里,就可以引出数论思想,所谓数论思想,就是通过数学公式或者数学定理又或者规律来求解问题
递归是很重要的一个知识点,也比较容易乱,所以,一定要仔细思考
我们继续来看一个很实际的问题
我要做核酸排队,大晚上的,不知道前面有多少人,听到喇叭在喊还可以做60个人,我想知道能不能轮到我,这个时候,就需要确认自己的位置,而我不知道我自己的位置
要想解决这个问题,我只需要问我前面的人,“你是第几个”,我再加一,就知道我是多少个了,如果我前面的不知道他自己是多少,他可以继续往前问,这样,最后还是回到我这里,我就知道我是第几个了
这个往前问的过程,就是‘递’,而前面人一个个传结果回来,就是‘归’,也可以称为回溯
我们可以用一个数学公式来标识 f(n) = f(n-1) + 1,f(n)是我的位置,而f(n-1)是我前面的人
其实简单点理解,就是自己调用自己
递归必须满足的条件
1、一个问题,必须可以分解为n个子问题,也就是分治思想,可以把一个大规模的问题,分解为多个小问题分别进行处理
2、拆分出的子问题,他们求解的思路过程是完全一样的
3、一定一定有一个最终的确定的结果,也就是说,一定要有一个递归的终止条件,否则,永远不会执行结束,你就会看到栈溢出异常
放到上面做核酸的问题,问前面的人是第几,可以看做是一个重复相同操作的子问题,而问到最前面的人,递归就会结束
递归的实现
我们来实现一下斐波那契数列
在开始前,我们先整理一下用递归实现斐波那契数列的条件
第一个,公式 f(n) = f(n-1) + f(n-2),第二个,终止条件,n <= 2,f(n) = 1
public static void main(String[] args) {
for (int i = 1; i < 21; i++) {
System.out.println("fb(i) = " + fb(i));
}
}
/**
* @Description: 递归-斐波那契数列
* @Author: create by YanXi on 2022/9/12 11:31
* @Email: [email protected]
*
* @param n
* @exception
* @Return: int
*/
public static int fb(int n) {
if (n <= 2) {
return 1;
} else {
return fb(n - 1) + fb(n - 2);
}
}我们在这个递归方法上,一定别忘了判断边界结束条件
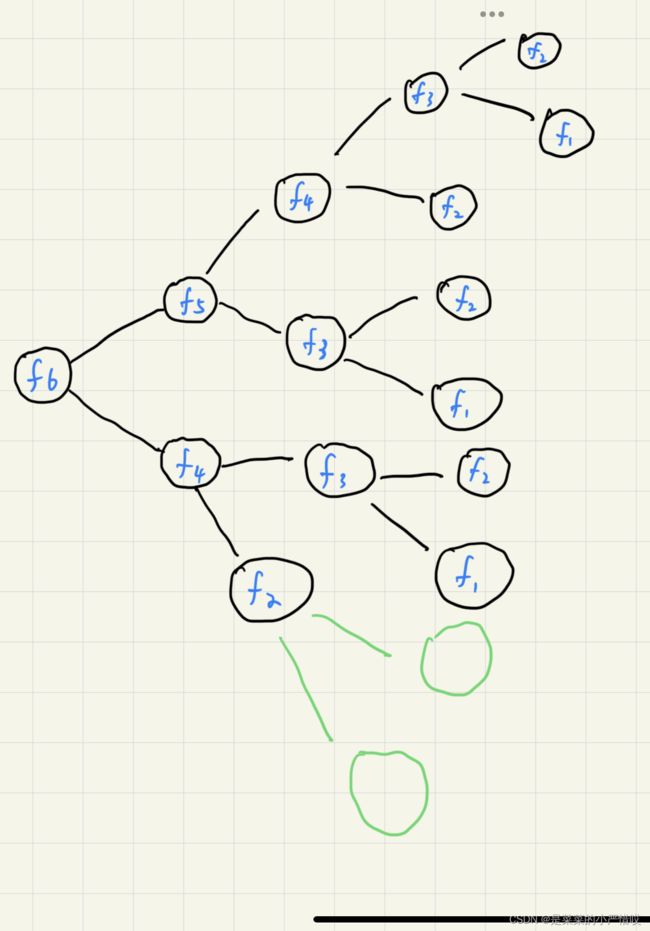
我们来想一下这个递归的时间复杂度是多少,为了方便看,我们画一下
我们算一下,假设 f2 后边还有,那么每一次运行,所需要的就是 1,2,4,8,可以发现,是2的n次方的时间复杂度
而之前我们排队做核酸的这个,明显的时间复杂度就是O(1)
我们再来看看空间复杂度
排队做核酸的空间复杂度我们思考一下,一个一个往下,并且这个节点不能回收,也就是说,一直往下,那就是n
而递归的空间复杂度,我们可以从上面的图看出来,空间复杂度和时间复杂度是一样的,都是2^n
递归的优化
我们既然知道了写的递归的时间复杂度是O(2^n),我们当然要想办法尽可能优化成线性关系
不用递归
首先最简单的,那肯定就是不用递归了
public static void main(String[] args) {
for (int i = 1; i < 21; i++) {
// System.out.println("fb(i) = " + fb(i));
System.out.println("fbN2(i) = " + fbN2(i));
}
}
/**
* @Description: 不用递归的斐波那契数列
* @Author: create by YanXi on 2022/9/12 13:04
* @Email: [email protected]
*
* @param n
* @exception
* @Return: int
*/
public static int fbN2(int n) {
if (n <= 2) {
return 1;
}
int f1 = 1;
int f2 = 1;
int f3 = 0;
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}很明显,时间复杂度就是O(n)
减少已执行次数
我们想一下,为什么这个递归的复杂度这么高
回头看看图,可以发现,走了好些次已经走过的动作,比如 f(3),走了好几次,那,我们是不是走过一次就不走第二次了,我们试试缓存起来
public static void main(String[] args) {
for (int i = 1; i < 21; i++) {
// System.out.println("fb(i) = " + fb(i));
// System.out.println("fbN2(i) = " + fbN2(i));
dataCache = new int[22];
System.out.println("fbN3(i) = " + fbN3(i));
}
}
static int[] dataCache = new int[0];
/**
* @Description: 减少重复执行次数的递归计算斐波那契数列
* @Author: create by YanXi on 2022/9/12 13:15
* @Email: [email protected]
*
* @param n
* @exception
* @Return: int
*/
public static int fbN3(int n) {
if (n <= 2) {
return 1;
} else if (dataCache[n] > 0) {
return dataCache[n];
} else {
// 没有执行过,所以计算完不能直接返回,先缓存一下,万一之后用呢
int result = fbN3(n - 1) + fbN3(n - 2);
dataCache[n] = result;
return result;
}
}尾递归
所谓尾递归,就是说调用函数一定出现在末尾,没有任何其他操作了,因为编译器在编译代码时如果发现函数末尾没有操作了,这个时候就不会创建新的栈,而是覆盖到前面去
我们实际来说一下,
return fb(n - 1) + fb(n - 2);
fb(n - 1)结束之后,还要参与一个加法运算,所以,这个结果就会入栈
那,我们可以把中间的结果传下去,到最后,也就结束了
public static void main(String[] args) {
for (int i = 1; i < 21; i++) {
// System.out.println("fb(i) = " + fb(i));
// System.out.println("fbN2(i) = " + fbN2(i));
// dataCache = new int[22];
// System.out.println("fbN3(i) = " + fbN3(i));
System.out.println("fbN4(i, 1, 1) = " + fbN4(i, 1, 1));
}
}
/**
* @Description: 尾递归
* @Author: create by YanXi on 2022/9/12 13:39
* @Email: [email protected]
*
* @param n
* @param result 上次结果
* @param pre 上上次的结果
* @exception
* @Return: int
*/
public static int fbN4(int n, int result, int pre) {
if (n <= 2){
// 因为结果带下来了,所以这儿不能返回1,而是返回结果
return result;
}
return fbN4(n - 1,result + pre , result);
}当然,这儿比较绕,尤其是最后尾递归这个参数
我们一个一个来看,第一个n我们肯定要传下去,不然我们都不知道到哪儿了,第二个,上次执行结果,是为了到达结束条件的时候,直接返回结果
注意,注意这儿,上次执行结果,是依赖于 f(n - 1) + f(n - 2)的
而 f(n - 1) 我们拿到了,还缺一个上上次结果,所以我们也要传下去上上次的结果
这样,我们就得到了递归函数的三个参数
写在最后
递归是一个看起来很简洁的写法,同时也是一个很容易混乱的写法,在实际使用中,一定要注意退出条件,如果想不明白,那就不要用递归,用循环或者其他方式去实现
而尾递归,重要的是想怎么往下传递,执行的结果不再返回到最后参与运算,也就是说,传到最后,就结束,不需要进行那么多次回溯的过程
关于尾递归,需要慢慢思考,以时间做积累,多看,多想,才能慢慢理解