《剑指Offer》模块三 思维题【面试官可能考的13道思维算法题】
思维题
1. 扑克牌的顺子【思维题】
原题链接
![]()
1. 判断所有牌中 是否出现 重复
2. 有序sort后 判断是否最大差距 <=4
class Solution {
public:
bool isContinuous( vector<int> nums) {
sort(nums.begin(), nums.end());
for (int i = 1; i < nums.size(); i ++ )
if (nums[i] && nums[i] == nums[i - 1])
return false;
for (auto x : nums)
if (x)
{
return nums.back() - x <= 4;
}
}
};
class Solution {
public boolean isContinuous(int[] nums) {
int n = nums.length;
if (n == 0) return false;
Arrays.sort(nums);
int k = 0;
while (nums[k] == 0) k++;
for (int i = k + 1; i < n; i++)
if (nums[i] == nums[i - 1])
return false;
return nums[n - 1] - nums[k] <= 4;
}
}
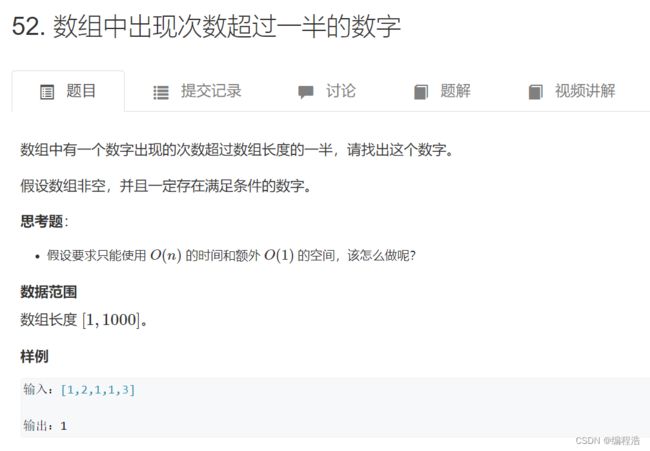
2. 数组中出现次数超过一半的数字
【面试题常考!!!】JZ39 数组中出现次数超过一半的数字【五种方法解决】
原题链接
class Solution {
public:
int moreThanHalfNum_Solution(vector<int>& nums) {
int cnt = 0, val = -1;
for (auto x : nums)
if (x == val)
cnt ++ ;
else
{
if (cnt) cnt -- ;
else
{
cnt = 1;
val = x;
}
}
return val;
}
};
class Solution {
public int moreThanHalfNum_Solution(int[] nums) {
int cnt = 0;
int val = 0;
for (int x : nums) {
if (cnt == 0) {
val = x;
cnt++;
} else {
if (val == x) {
cnt++;
} else {
cnt--;
}
}
}
return val;
}
}
3. 最小的k个数
class Solution {
public:
vector<int> getLeastNumbers_Solution(vector<int> input, int k) {
sort(input.begin(),input.end());
input.erase(input.begin() + k,input.end());
return input;
}
};
class Solution {
public List<Integer> getLeastNumbers_Solution(int [] input, int k) {
Arrays.sort(input);
List<Integer> ret = new LinkedList();
for(int i = 0; i < k; i++){
ret.add(input[i]);
}
return ret;
}
}
优先队列
class Solution {
public List<Integer> getLeastNumbers_Solution(int [] input, int k) {
LinkedList<Integer> res = new LinkedList<>();
PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->(b-a));
for(int n : input){
pq.offer(n);
if(pq.size() > k) pq.poll();
}
while(!pq.isEmpty()){
res.addFirst(pq.poll());
}
return res;
}
}
4. 从1到n整数中1出现的次数
原题链接
![]()
class Solution {
public:
int numberOf1Between1AndN_Solution(int n) {
if (!n) return 0;
vector<int> number;
while (n) number.push_back(n % 10), n /= 10;
long long res = 0;
for (int i = number.size() - 1; i >= 0; i -- )
{
int left = 0, right = 0, t = 1;
for (int j = number.size() - 1; j > i; j -- ) left = left * 10 + number[j];
for (int j = i - 1; j >= 0; j -- ) right = right * 10 + number[j], t *= 10;
res += left * t;
if (number[i] == 1) res += right + 1;
else if (number[i] > 1) res += t;
}
return res;
}
};
5. 数字序列中某一位的数字【数位统计】
原题链接
![]()
class Solution {
public:
int digitAtIndex(int n) {
long long i = 1, s = 9, base = 1;//i表示是几位数,s表示位数共有多少个,base表示位数的起始值。
while(n > i * s) { // 9, 90, 900, 9000, 90000, i * s表示位数总共占多少位。
n -= i * s; // 1000 - 9 - 90 * 2 - 900 * 3 ,当i= 3 时不符合条件,说明是在三位数里面。
i ++;
s *= 10;
base *= 10;
}
int number = base + (n + i - 1) / i - 1; //求位数的第几个数, 1000 - 9 - 180 = n , n / 3 + base - 1(考虑0故减1), 向上取整 n + i - 1。
int r = n % i ? n % i : i; // 除不尽就是第几位,除尽力了就是最后一位。
for (int j = 0; j < i - r; j ++) number /= 10; //求数的第i - r位,取出第i - r位。
return number % 10;
}
};
6. 把数组排成最小的数【比较器】
原题链接
![]()
本题
a+b 和 b+a从小到大排序
class Solution {
public:
static bool cmp(string a, string b)
{
return a + b < b + a;
}
string printMinNumber(vector<int>& nums) {
vector<string> num_strs;
for (auto num : nums) num_strs.push_back(to_string(num));
sort(num_strs.begin(), num_strs.end(), cmp);
string res;
for (auto num : num_strs) res += num;
return res;
}
};
// import java.util.*;
class Solution {
static Comparator<Integer> cmp = new Comparator<Integer>() {
@Override
public int compare(Integer o1,Integer o2) {
String s1 = o1+""+o2;
String s2 = o2+""+o1;
return s1.compareTo(s2);
}
};
public String printMinNumber(int[] nums) {
String res = "";
Integer[] list = new Integer[nums.length];
int n = nums.length;
for(int i = 0; i < n; i++){
list[i] = nums[i];
}
Arrays.sort(list,cmp);
for(int i = 0; i < n; i++){
res += list[i]+"";
}
return res;
}
}
7. 不用加减乘除做加法【二进制 加法】
原题链接
int sum = num1 ^ num2;//不进位的加法
int carry = (num1 & num2)<<1;//进位
![]()
class Solution {
public:
int add(int num1, int num2){
while(num2!=0){
int sum = num1 ^ num2;//不进位的加法
int carry = (num1 & num2)<<1;//进位
num1 = sum;
num2 = carry;
}
return num1;
}
};
class Solution {
public int add(int num1, int num2) {
while (num2 != 0) {
int notCarry = num1 ^ num2;
int Carry = (num1 & num2) << 1;
num1 = notCarry;
num2 = Carry;
}
return num1;
}
}
8. 构建乘积数组
原题链接
![]()
(动归) O(n)
用两个数组left和right,left[i]=A[0]A[1]…*A[i-1], left[i]=A[i-1]*left[i-1]; right[i] = A[i+1]A[i+2]…*A[n-1],则right[i]=A[i+1]*right[i+1]。
最后结果B[i]=left[i]*right[i]。
时间复杂度分析:需要遍历数组,复杂度为O(n)
class Solution {
public:
vector<int> multiply(const vector<int>& A) {
vector<int>left(A.size(),1);
vector<int>right(A.size(),1);
for(int i = 1;i<A.size();i++){
left[i] = A[i-1]*left[i-1];
}
for(int i = A.size()-2;i>=0;i--){
right[i] = A[i+1]*right[i+1];
}
vector<int>B(A.size(),0);
for(int i = 0;i<A.size();i++){
B[i] = left[i]*right[i];
}
return B;
}
};
9. 找出数组中重复的数字
原题链接
![]()
普通思路
我想的是创建一个数组,大小为1010个
然后遍历一遍数组,记录数据出现的个数,如果个数超过1,那么就是重复数据
时间复杂度O(n*logn) 也就是排序的时间复杂度
优化思路
由于本题给了一个限制
所有数据,一定在 0-n-1 之间
也就是比如n是5
最偏激出现的可能就是
0 1 2 3 4 这样的数据
但凡出现一个重复的
那么就是
0 0 1 2 3
问题来了
如何简便的找出重复数据呢?
我们可以这样
比如所给样例为
3 2 1 0 0
第一个数据是3
3 2 1 0 0
i
0 2 1 3 0
i
当把i所指的元素替换成自己角标的数值
0 2 1 3 0
i
0 1 2 3 0
i
0 1 2 3 0
i
此时再替换就出现重复
因为0位置上已经有0
这个思路归结于
所有的数据大小在 0 - n-1 之间
class Solution {
public:
int duplicateInArray(vector<int>& nums) {
int n = nums.size();
for (auto x : nums)
if (x < 0 || x >= n)
return -1;
for (int i = 0; i < n; i ++ ) {
while (nums[nums[i]] != nums[i]) swap(nums[i], nums[nums[i]]);
if (nums[i] != i) return nums[i];
}
return -1;
}
};
10. 不修改数组找出重复的数字
原题链接
![]()
两个错误的普通思路
错误1(空间复杂度不满足)
- 创建一个1010大小的数组A
- 遍历原数组
- ++A[nums[i]]
- 如果A[nums[i]] > 1那么说明重复
错误2(改变了原数组)
- 给原数组从小到大排序
- 然后遍历每每相邻的两个元素,看其是否相等.
- 因为重复的元素一定相等,一定挨着
普通方法(双重循环)
class Solution {
public:
int duplicateInArray(vector<int>& nums) {
for(int i = 0; i < nums.size(); i++)
for(int j = 0; j < nums.size(); j++)
{
if(i==j)
continue;
if(nums[i]==nums[j])
return nums[i];
}
}
};
优化方法(优化循环次数,减去一下不需要循环的数据)
由于所给数据范围是1-n
而数据的长度是n+1
所以一定会出现重复数据的
这种类型题,学过抽屉原理的,应该会明白这道题可以用抽屉原理思考,
关于抽屉原理可以在csdn查一下,就懂了
那么,如何利用抽屉原理思考呢?
![]()
需要注意的一点是
当我们计算出大于mid的个数后
是与n-mid-1的大小进行比较,划分区间(理由是这样才能满足抽屉原理)
class Solution {
public:
int duplicateInArray(vector<int>& nums) {
int n = nums.size();
// cout << n ;
int l = 1,r = n-1;
while(l<r)
{
int mid = (l + r)>> 1;
int cnt = 0;
for(auto x:nums)
if(x>mid)
cnt++;
if(cnt > (n-1-mid))
{
l = mid+1;
}
else
{
r = mid;
}
}
return r;
}
};
11. 二维数组中的查找
原题链接
![]()
普通思路
我的想法是从左上角开始往右下角遍历
但是行不通,
总结就是必须好好观察样例,找到特点规律性质
精彩思路
![]()
class Solution {
public:
bool searchArray(vector<vector<int>> array, int target) {
if (array.empty() || array[0].empty()) return false;
int i = 0, j = array[0].size() - 1;
while (i < array.size() && j >= 0) {
if (array[i][j] == target) return true;
if (array[i][j] > target) j -- ;
else i ++ ;
}
return false;
}
};
12. 替换空格
原题链接
简单题,遍历字符串可以用for(auto : )
![]()
class Solution {
public:
string replaceSpaces(string &str) {
string end;
for(auto x:str)
{
if(x!=' ')
end+=x;
else
end+="%20";
}
return end;
}
};
13. 旋转数组的最小数字
![]()
原题链接
class Solution {
public:
int findMin(vector<int>& nums) {
if(nums.size() == 0)
return -1;
if(nums.size() == 1)
return nums[0];
for(int i = 0; i < nums.size()-1; i++)
{
if(nums[i] > nums[i+1])
{
return nums[i+1];
}
}
return nums[0];
}
};