二叉查找树
二叉查找树
简介
二叉查找树(Binary Search Tree,BST),又叫做二叉排序树、二叉搜索树,是一种对查找和排序都有用的特殊二叉树。
二叉查找树或是空树,或是满足如下三个性质的二叉树:
- 若其左子树非空,则左子树上所有节点的值都小于根节点的值
- 若其右子树非空,则右子树上所有节点的值都大于根节点的值
- 其左右子树都是一棵二叉查找树
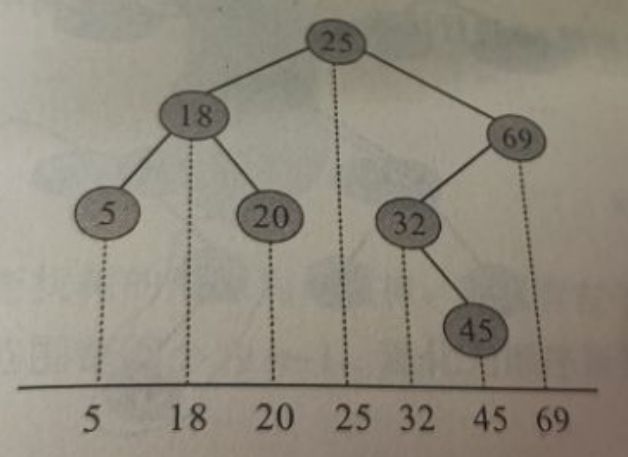
二叉查找树的特性:左子树<根<右子树,即二叉查找树的中序遍历是一个递增序列。
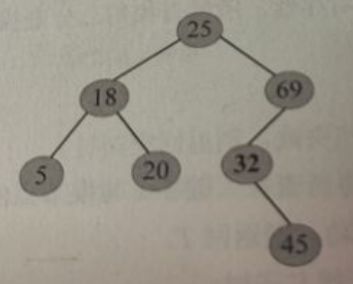
如下图所示,其中序遍历为{5,18,29,25,32,25,69}
我们来定义一下二叉查找树的数据结构:
typedef struct BSTNode{
int data; //节点数据域
BSTNode *lchild,*rchild; //左孩子指针 右孩子指针
}BSTNode,*BSTree;
也就是说我们用类型BSTNode代替了类型struct BSTNode,用类型BSTree代替了类型struct BSTNode*,此时就要注意了BSTree就是一个指针类型哦
二叉查找树的查询
因为二叉查找树的中序遍历有序性,即得到的递增的序列,由于有序,因此其查找与二分查找类似,每次都可以缩小查找范围,查询效率较高。
算法步骤:
- 若二叉查找树为空,则查找失败,返回空指针
- 若二叉查找树非空,则将待查找关键字key与根节点的关键字 T − > d a t a T->data T−>data进行比较:
- 如果 x = T − > d a t a x=T->data x=T−>data,则查找成功,返回查询到的当前节点T
- 如果 x < T − > d a t a x
data x<T−>data,则递归查找左子树 - 如果 x > T − > d a t a x>T->data x>T−>data,则递归查找右子树
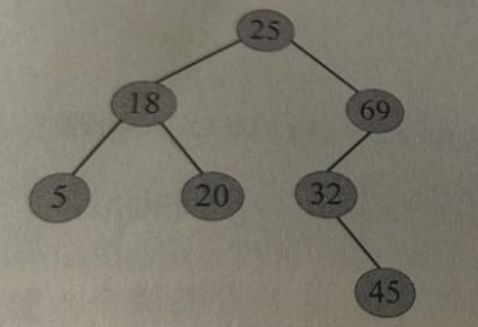
如下图所示,查找关键字32:
(1)将32与二叉查找树的树根25比较,发现 32 > 25 32>25 32>25,于是到右子树中查询,如下图所示:
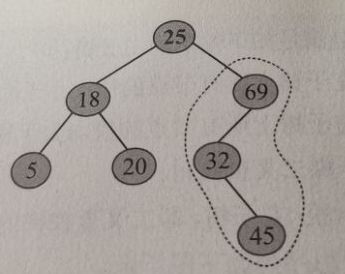
(2)将32与右子树的树根69比较,发现 32 < 69 32<69 32<69,于是到左子树中查询,如下图所示:
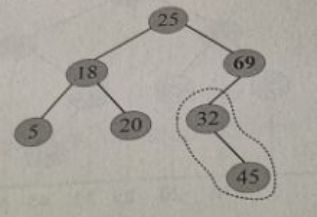
(3)将32与左子树的树根32比较,发现 32 = 32 32=32 32=32,相等,查询成功,返回该节点的指针,如下图所示:
代码:
//二叉排序树的递归查找
BSTree find(BSTree T,int key)
{
//如果二叉排序树为空则返回T为NULL 或者查找成功则返回指向该数据元素结点的指针
if(!T||T->data==key)
return T;
//递归查找左子树
else if(keydata)
return find(T->lchild,key);
//递归查找右子树
else
return find(T->rchild,key);
}
算法分析:
- 时间复杂度:最好情况是 O ( l o g n ) O(logn) O(logn),最坏情况是 O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
二叉查找树的插入
因为二叉查找树的中序遍历存在有序性,所以首先要查找待插入元素的插入位置,当查找不成功时再将待插入元素作为新的叶子节点成为最后一个查找节点的左孩子或者右孩子。
算法步骤:
- 若二叉查找树为空,则创建一个新的节点 S S S,将待插入关键字放入新节点的数据域,然后将 S S S节点作为根节点, S S S节点的左右子树都设置为空。
- 若二叉查找树非空,则将带插入元素e和根节点的关键字 T − > d a t a T->data T−>data比较:
- 如果 e < T − > d a t a e
data e<T−>data,则将 e e e插入到左子树中 - 如果 e > T − > d a t a e>T->data e>T−>data,则将 e e e插入到右子树中
- 如果 e < T − > d a t a e
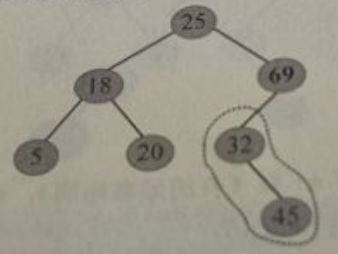
如图,向其中插入元素30:
(1)将30与根节点25比较,发现 25 < 30 25<30 25<30,因此到右子树中查询,如下图:
(2)将30与右子树的树根69比较,发现 30 < 69 30<69 30<69,则到69的左子树中查询,如下图:
(3)将30与左子树的树根32比较,发现 30 < 32 30<32 30<32,在32的左子树中查找,如下图:
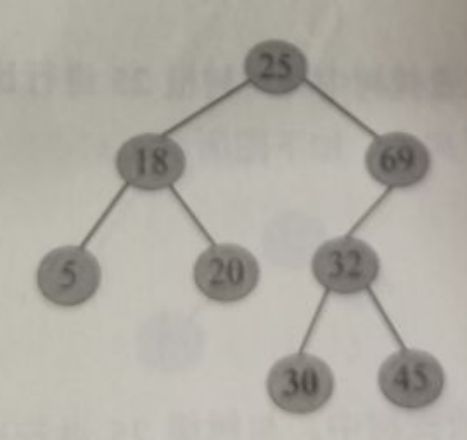
(4)将30作为新的叶子节点插入到32的左子树中,如下图:
代码:
//二叉排序树的插入
void insert(BSTree &T,int e)
{
//如果二叉查找树为空
if(!T)
{
//则创建一个新的节点S
BSTree S=new BSTNode;
//将待插入关键字e放入新节点S的数据域中
S->data=e;
//新节点S的左右子树都为空
S->lchild=S->rchild=NULL;
//将新节点S作为根节点
T=S;
}
//如果二叉排序树非空 则将待插入关键字e与根节点的关键字T->data比较
//如果edata,则说明应该将x插入到左子树中
else if(edata)
insert(T->lchild,e);
//如果e>T->data,则说明应该将x插入到右子树中
else if(e>T->data)
insert(T->rchild,e);
}
算法分析:
在二叉查找树中进行插入操作时需要先查找插入位置,插入本身只需要常数时间,但是查找插入位置的时间复杂度为 O ( l o g n ) O(logn) O(logn)
二叉查找树的创建
二叉查找树的创建可以从空树开始,按照输入关键字的顺序依次进行插入操作,最终得到一棵二叉查找树。
算法步骤:
- 初始化二叉查找树为空树, T = N U L L T=NULL T=NULL
- 输入一个关键字 e e e,将 e e e插入到二叉查找树T中
- 重复步骤2,直到关键字输入完毕。
代码:
//二叉排序树的创建
//二叉查找树的创建可以从空树开始 按照输入关键字的顺序依次进行插入操作 最终得到一棵二叉排序树
void build(BSTree &T)
{
T=NULL; //从空树开始 初始化二叉排序树为空树
int e;
//每输入一个节点
while(cin>>e,e!=-1)
{
insert(T,e); //则把该节点插入到二叉排序树中
}
}
算法分析:
有 n n n个即将插入的元素,因此二叉查找树的创建需要 n n n次插入,每次插入在最好情况和平均情况下都需要 O ( l o g n ) O(logn) O(logn)时间,在最坏情况需要 O ( n ) O(n) O(n)时间,因此在最好情况和平均情况下的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),最坏情况下的时间复杂度为 O ( n 2 ) O(n^2) O(n2)
创建二叉查找树时,输入序列的次序不同, 创建的二叉查找树也是不同的。
二叉查找树的删除
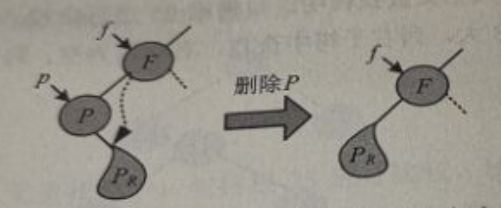
首先在二叉查找树中找到待删除节点,然后执行删除操作。假设指针p指向待删除节点,指针f指向p的父节点。根据待删除节点所在位置的不同,删除操作的处理方法也不同,可以分为以下三种情况:
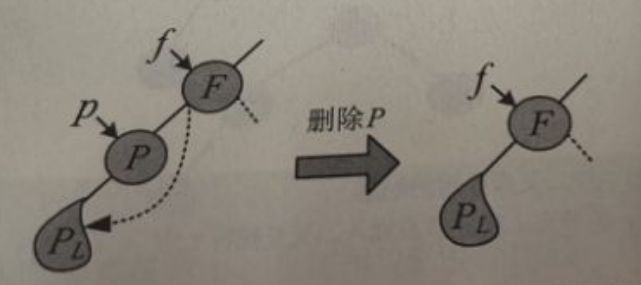
(1)被删除节点的左子树为空:那么令其右子树子承父业代替被删除节点的位置即可。
如下图所示:
(2)被删除节点的右子树为空:那么令其左子树子承父业代替被删除节点的位置即可。
如下图所示:
(3)被删除节点的左右子树都不为空:如果被删除节点的左右子树都不为空,那么就不能采用子承父业的方法了。根据二叉查找树的中序遍历有序性,删除该节点,可以利用其直接前驱或者直接后继来代替被删除节点的位置,然后删除其直接前驱或者其直接后继即可。
那么在中序遍历中,一个节点的直接前驱或者直接后继是哪个节点呢?
其实 x x x的直接前驱就是那些 < x
- 直接前驱:在中序遍历中,节点p的直接前驱就是其左子树中的最右节点。即沿着p的左子树一直访问其右子树,直到没有右子树,这样就找到了最右节点,也就是直接前驱。如图a
- 直接后继:在中序遍历中,节点p的直接后继就是其右子树中的最左节点。即沿着p的右子树一直访问其左子树,直到没有左子树,这样就找到了最左节点,也就是直接后继。如图b
以找直接前驱为栗子:在二叉查找树中删除24。首先找到24的位置p,然后找到p的直接前驱s(22),把22赋值给p的数据域,删除s,删除过程如下图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RK0fgKUd-1630048204711)(https://cdn.jsdelivr.net/gh//3CodeLove/Images@main/20210827140927.png)]
删除节点之后是不是仍然满足二叉查找树的中序遍历有序性呢?
需要注意的是,有一种特殊情况,即p的左孩子没有右子树,s就是其左子树的最右节点(直接前驱),即s代替p,然后删除s即可。因为s为最右节点且没有右子树,删除后,左子树子承父业。
举个栗子:在二叉查找树中删除20,删除过程如下图所示,由图可知,20的左孩子是8,8没有右子树了,那么8就是20的左子树的最右节点了,即8是20的直接前驱。
算法步骤:
- 在二叉查找树中查找待删除关键字的位置,p指向待删除节点,f指向p的父节点。如果查找失败,则返回
- 如果查找成功,则分为三种情况进行删除操作:
- 如果被删除节点的左子树为空,则令其右子树子承父业代替其位置即可
- 如果被删除节点的右子树为空,则令其左子树子承父业代替其位置即可
- 如果被删除节点的左右子树都不为空,则令其直接前驱或者直接后继代替它,再删除其直接前驱或者直接后继即可
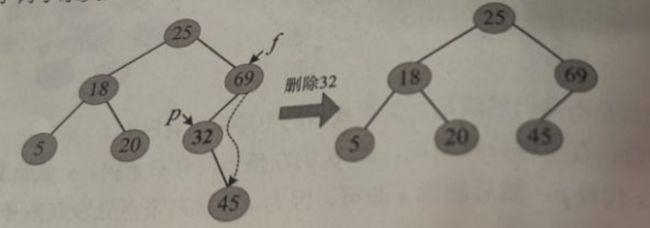
(1)左子树为空。在二叉查找树中删除32,首先查找到32所在的位置,判断其左子树为空,则令其右子树子承父业代替其位置,删除过程如下图:
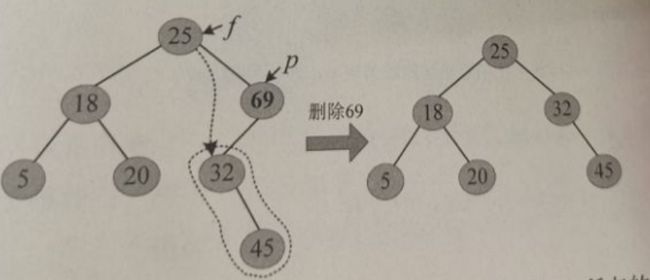
(2)右子树为空。在二叉查找树中删除69,首先查找到69所在的位置,判断其右子树为空,则令其左子树子承父业代替其位置,删除过程如下图:
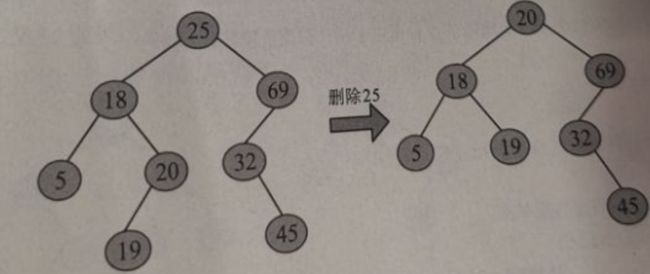
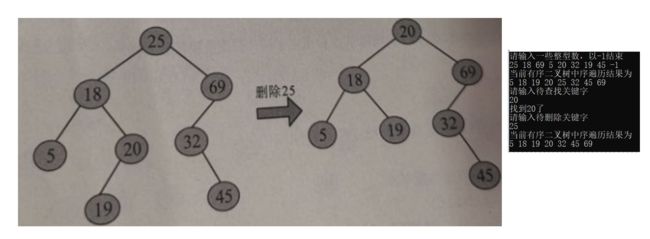
(3)左右子树都不为空。在二叉查找树中删除25,首先查找到25所在的位置,判断其左右子树都不为空,则令其直接前驱(左子树最右节点是20)代替它,在删除其直接前驱20,删除20时i,其左子树代替其位置。删除过程如下图所示:
二叉查找树的删除操作较为复杂,代码要结合上面的图示理解
代码:
//二叉排序树的删除
void del(BSTree &T,int key)
{
//从二叉排序树T中删除关键字等于key的结点
BSTree p=T;
BSTree f=NULL;
BSTree q,s;
if(!T) return; //树为空则返回
while(p)//查找
{
if(p->data==key)
break; //找到关键字等于key的结点p,结束循环
f=p; //f为p的双亲
if (p->data>key)
p=p->lchild; //在p的左子树中继续查找
else
p=p->rchild; //在p的右子树中继续查找
}
if(!p)
return; //找不到被删结点则返回
//三种情况:p左右子树均不空、无右子树、无左子树
if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空
{
q=p;
s=p->lchild;
while(s->rchild)//在p的左子树中继续查找其前驱结点,即最右下结点
{
q=s;
s=s->rchild;
}
p->data=s->data; //s的值赋值给被删结点p,然后删除s结点
if(q!=p)
q->rchild=s->lchild; //重接q的右子树
else
q->lchild=s->lchild; //重接q的左子树
delete s;
}
else
{
if(!p->rchild)//被删结点p无右子树,只需重接其左子树
{
q=p;
p=p->lchild;
}
else if(!p->lchild)//被删结点p无左子树,只需重接其右子树
{
q=p;
p=p->rchild;
}
/*――――――――――将p所指的子树挂接到其双亲结点f相应的位置――――――――*/
if(!f)
T=p; //被删结点为根结点
else if(q==f->lchild)
f->lchild=p; //挂接到f的左子树位置
else
f->rchild=p;//挂接到f的右子树位置
delete q;
}
}
算法分析:
二叉查找树的删除主要是查找的过程,需要 O ( l o g n ) O(logn) O(logn)时间。在删除过程中,如果需要查找被删除节点前驱,则也需要 O ( l o g n ) O(logn) O(logn)时间。所以,在二叉查找树中进行删除操作的时间复杂度为 O ( l o g n ) O(logn) O(logn)
完整代码
以下面这幅图为例子在DevC++上测试:
#include
#include
#include
using namespace std;
typedef struct BSTNode{
int data; //节点数据域
BSTNode *lchild,*rchild; //左孩子指针 右孩子指针
}BSTNode,*BSTree;
//二叉排序树的插入
void insert(BSTree &T,int e)
{
//如果二叉查找树为空
if(!T)
{
//则创建一个新的节点S
BSTree S=new BSTNode;
//将待插入关键字e放入新节点S的数据域中
S->data=e;
//新节点S的左右子树都为空
S->lchild=S->rchild=NULL;
//将新节点S作为根节点
T=S;
}
//如果二叉排序树非空 则将待插入关键字e与根节点的关键字T->data比较
//如果edata,则说明应该将x插入到左子树中
else if(edata)
insert(T->lchild,e);
//如果e>T->data,则说明应该将x插入到右子树中
else if(e>T->data)
insert(T->rchild,e);
}
//二叉排序树的创建
//二叉查找树的创建可以从空树开始 按照输入关键字的顺序依次进行插入操作 最终得到一棵二叉排序树
void build(BSTree &T)
{
T=NULL; //从空树开始 初始化二叉排序树为空树
int e;
//每输入一个节点
while(cin>>e,e!=-1)
{
insert(T,e); //则把该节点插入到二叉排序树中
}
}
//中序遍历 原则:左根右
void InOrderTraverse(BSTree &T)
{
if(T)
{
InOrderTraverse(T->lchild); //左
printf("%d ",T->data); //根
InOrderTraverse(T->rchild); //右
}
}
//二叉排序树的递归查找
BSTree find(BSTree T,int key)
{
//如果二叉排序树为空则返回T为NULL 或者查找成功则返回指向该数据元素结点的指针
if(!T||T->data==key)
return T;
//递归查找左子树
else if(keydata)
return find(T->lchild,key);
//递归查找右子树
else
return find(T->rchild,key);
}
//二叉排序树的删除
void del(BSTree &T,int key)
{
//从二叉排序树T中删除关键字等于key的结点
BSTree p=T;
BSTree f=NULL;
BSTree q,s;
if(!T) return; //树为空则返回
while(p)//查找
{
if(p->data==key)
break; //找到关键字等于key的结点p,结束循环
f=p; //f为p的双亲
if (p->data>key)
p=p->lchild; //在p的左子树中继续查找
else
p=p->rchild; //在p的右子树中继续查找
}
if(!p)
return; //找不到被删结点则返回
//三种情况:p左右子树均不空、无右子树、无左子树
if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空
{
q=p;
s=p->lchild;
while(s->rchild)//在p的左子树中继续查找其前驱结点,即最右下结点
{
q=s;
s=s->rchild;
}
p->data=s->data; //s的值赋值给被删结点p,然后删除s结点
if(q!=p)
q->rchild=s->lchild; //重接q的右子树
else
q->lchild=s->lchild; //重接q的左子树
delete s;
}
else
{
if(!p->rchild)//被删结点p无右子树,只需重接其左子树
{
q=p;
p=p->lchild;
}
else if(!p->lchild)//被删结点p无左子树,只需重接其右子树
{
q=p;
p=p->rchild;
}
/*――――――――――将p所指的子树挂接到其双亲结点f相应的位置――――――――*/
if(!f)
T=p; //被删结点为根结点
else if(q==f->lchild)
f->lchild=p; //挂接到f的左子树位置
else
f->rchild=p;//挂接到f的右子树位置
delete q;
}
}
int main()
{
BSTree T; //整棵二叉排序树的根节点
puts("请输入一些整型数,以-1结束");
//建立一棵二叉排序树
build(T);
puts("当前有序二叉树中序遍历结果为");
//对这棵二叉排序树进行中序遍历
InOrderTraverse(T);
puts("");
int key;
puts("请输入待查找关键字");
scanf("%d",&key);
//在二叉排序树查找关键字key
BSTree ans=find(T,key);
//查找成功
if(ans)
printf("找到%d了\n",key);
else //查找失败
printf("没有找到%d\n",key);
puts("请输入待删除关键字");
scanf("%d",&key);
//在二叉排序树中删除关键字key
del(T,key);
puts("当前有序二叉树中序遍历结果为");
//对删除节点后的这棵二叉排序树进行中序遍历
InOrderTraverse(T);
return 0;
}