背包问题、决策树及python实现

背包问题是最优解问题中的一种，我们先来看一下最优解的定义：在特定条件限制下，按特定需求得出最优结果。

按照这个定义我们做一下下面的分析，有以下一些特征：

• 特定条件限制，比如：某一个空间有固定容量，或固定负重，不可以超出
• 特定需求，需要放入多个多种类型东西，这些东西有重量、价值、体积等属性
• 最优结果，比如：最大价值，最多数量等

举一个例子：

某个小偷半夜潜入某户人家偷盗，这家人家有四样值钱的东西ABCD，ABC的重量分别是｛5,3,2｝，价值分别是｛9,7,8｝，小偷的背包只能放下5磅的东西，请问小偷应该拿那几样？

分析问题：

拿到算法题第一思路，简化问题。
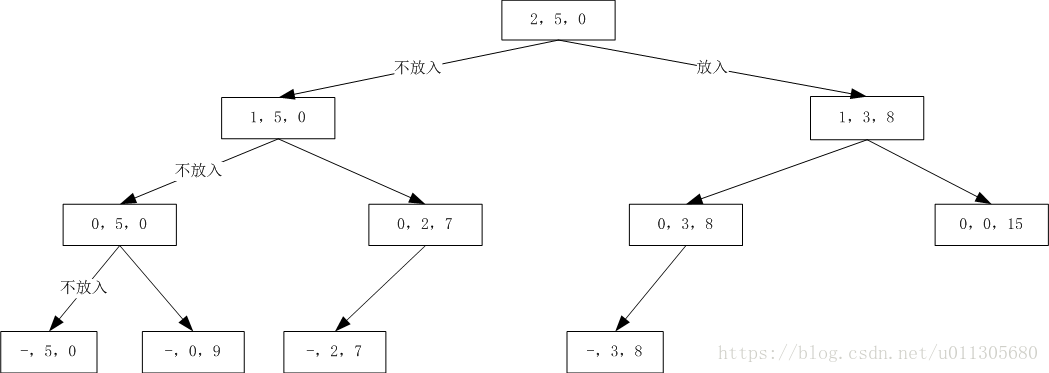
首先我们决定C这个物品放不放，有两个选择，选择的结果是不放我们还有5磅的剩余重量当前价值为0，放了就只有3磅当前价值为8。如果不放，我们来决定是否放B，不放我们还有8磅价值为0，放了还有2磅当前价值为7；如果放了C，那我们如果再决定是否放B，如果不放，还有3磅当前价值8，如果放了还有0磅当前价值15。依此类推，可以看出这是一棵二叉树，这就是我们的决策树

每个节点包含3个数据：Index,surplusWeight,totalValue，index是当前判断的节点的索引，我们从右开始，也就是2；surplusWeight表示当前剩余可放重量；totalValue表示当前已放物品总价值。
在分析前，我们遵循两个原则：最左优先，深度优先；然后采用回溯（backtrack）来生成这颗决策树。作分叉的时候向左表示不放当前节点索引的物品，向右表示放当前节点索引的物品。

1. 第一个节点(2,5,0)，生成左节点表示不放入第三个物品，也就是C，那么左节点是(1,5,0)，表示还剩5磅重量可以放，当前总价值0；
2. (1,5,0)节点继续向左分，表示不放入B，生成节点(0,5,0)；(0,5,0)继续向左分，表示不放入A，生成节点(-,5,0)，结束！
3. 我们开始回溯，回溯到上一个节点(0,5,0)，开始向右分，生成(-,0,9)，结束！
4. 再向上回溯到(1,5,0)，向右分，放入B，生成(0,2,7)；再向左分，生成(-,2,7)；结束！
5. 向上回溯到(0,2,7)，由于只剩下2磅的物体可以放，而0是5磅，所以这个节点没有右结点，只能继续回溯到根节点(2,5,0)，开始向右分，生成(1,3,8)，向左分生成(0,3,8)(-,3,8)，结束！
6. 向上回溯到(0,3,8)，由于0是5磅，所以(0,3,8)没有右结点，继续向上回溯到(1,3,8)，生成右节点(0,0,15)，没有剩余重量了，结束！
   
   从树上我们可以看出最优结果是BC放入，A不放入，最大价值为15。但是我们怎么在程序中实现呢？
   从图中我们可以看出每个非叶子节点的最优值其实是左右两个节点的最优值的较大值，这其实就是决策树的本质了！！！最后根节点的最优值就是整个树的最优值，所以我们可以开始写代码了，如下：

# -*- coding: utf-8 -*-
#dicision tree
def maxVal(w,v,i,aw):
    print 'maxVal called with:',i,aw
    global numCalls
    numCalls+=1
    if i==0:
        if w[i]<=aw:return v[i]
        else:return 0
    without_i=maxVal(w,v,i-1,aw)
    if w[i]>aw:
        return without_i
    else:
        with_i = v[i]+maxVal(w,v,i-1,aw-w[i])
    return max(with_i,without_i)  #最优值为左节点与右节点对比之后的较大值

weights=[5,3,2]
vals=[9,7,8]
numCalls=0
res=maxVal(weights,vals,len(vals)-1,5)
print 'max val = ',res,'number of calls =',numCalls
print 
weights=[1,5,3,4]
vals=[15,10,9,5]
numCalls=0
res=maxVal(weights,vals,len(vals)-1,8)
print 'max val = ',res,'number of calls =',numCalls
# weights=[1,1,5,5,3,3,4,4]
# vals=[15,15,10,10,9,9,5,5]
# numCalls=0
# res=maxVal(weights,vals,len(vals)-1,8)
# print 'max val = ',res,'number of calls =',numCalls

执行结果：

D:\python>python knapsacks.py
maxVal called with: 2 5
maxVal called with: 1 5
maxVal called with: 0 5
maxVal called with: 0 2
maxVal called with: 1 3
maxVal called with: 0 3
maxVal called with: 0 0
max val =  15 number of calls = 7

maxVal called with: 3 8
maxVal called with: 2 8
maxVal called with: 1 8
maxVal called with: 0 8
maxVal called with: 0 3
maxVal called with: 1 5
maxVal called with: 0 5
maxVal called with: 0 0
maxVal called with: 2 4
maxVal called with: 1 4
maxVal called with: 0 4
maxVal called with: 1 1
maxVal called with: 0 1
max val =  29 number of calls = 13
#maxVal called with: 7 8
#... ...
#maxVal called with: 1 3
#maxVal called with: 0 3
#maxVal called with: 0 2
#... ...
#maxVal called with: 1 3
#maxVal called with: 0 3
#maxVal called with: 0 2
#... ...
#maxVal called with: 5 4
#maxVal called with: 4 4
#maxVal called with: 3 4
#... ...
#maxVal called with: 5 4
#maxVal called with: 4 4
#maxVal called with: 3 4
#max val =  48 number of calls = 85

可以看出执行了7次，改成4个物品参数后执行次数为13次，改成8个物品之后是85次。从85次的执行日志可以看出，有很多重复的递归，其实是可以消除的，这个我们叫做“重叠子问题（overlapping sub problems）”，可以通过默记法(memoization) 避免多余的计算。代码如下：

#memoization resolve overlapping sub problems
#默记法解决重叠子问题
def fastMaxVal(w,v,i,aw,m):
    # print 'maxVal called with:',i,aw,m
    global numCalls
    numCalls+=1
    try:
        return m[(i,aw)]
    except KeyError:
        if i==0:
            if w[i]<=aw:
                m[(i,aw)]=v[i]
                return v[i]
            else:
                m[(i,aw)]=0
                return 0
        without_i=fastMaxVal(w,v,i-1,aw,m)
        if w[i]>aw:
            m[(i,aw)]=without_i
            return without_i
        else:
            with_i = v[i]+fastMaxVal(w,v,i-1,aw-w[i],m)
        res=max(with_i,without_i)
        m[(i,aw)]=res
        return res
def maxVal0(w,v,i,aw):
    m={}
    return fastMaxVal(w,v,i,aw,m)

weights=[1,5,3,4]
vals=[15,10,9,5]
numCalls=0
res=maxVal0(weights,vals,len(vals)-1,8)
print 'max val = ',res,'number of calls =',numCalls
# weights=[1,1,5,5,3,3,4,4]
# vals=[15,15,10,10,9,9,5,5]
# numCalls=0
# res=maxVal0(weights,vals,len(vals)-1,8)
# print 'max val = ',res,'number of calls =',numCalls

执行结果：

max val =  29 number of calls = 13
max val =  48 number of calls = 50

从执行结果可以看出n=4的时候并没有减少工作量，但是n=8的时候减少到了50，n越大，优化效果越好。但是有一个需要注意的地方，这个地方m[(i,aw)]的key是i和aw组成的元组。因为i能代表整个一层子节点，所以需要加上aw进一步区分。