SSD目标检测原理详解

论文：SSD: Single Shot MultiBox Detector
代码：https://github.com/weiliu89/caffe/tree/ssd

1. 目标检测简介

当前主流的目标算法主要分为两个类型：
（1）two-stage方法，如R-CNN系算法，其主要思路是先通过启发式方法（selective search）或者CNN网络（RPN）产生一系列稀疏的候选框，然后对这些候选框进行分类与回归，two-stage方法的优势是准确度高；
（2）one-stage方法，如Yolo和SSD，其主要思路是均匀地在图片的不同位置进行密集抽样，抽样时可以采用不同尺度和长宽比，然后利用CNN提取特征后直接进行分类与回归，整个过程只需要一步，所以其优势是速度快，但是均匀的密集采样的一个重要缺点是训练比较困难，这主要是因为正样本与负样本（背景）极其不均衡，导致模型准确度稍低。
不同算法的性能如图1所示，可以看到两类方法在准确度和速度上的差异

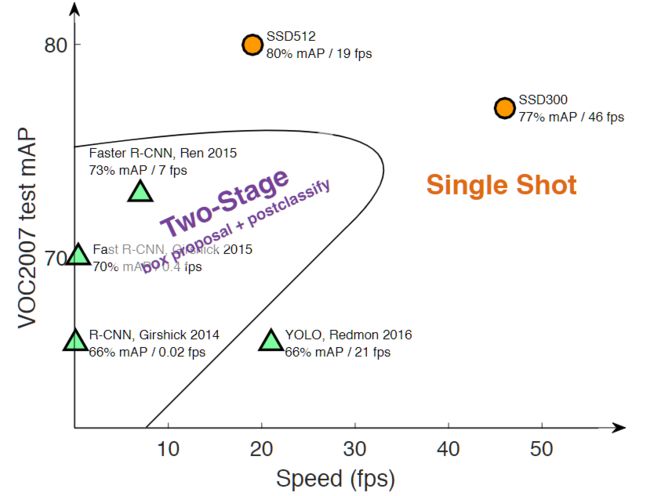
其中SSD512是指输入图片为 $512\times 512$，同理SSD300为输入图片 是$300\times 300$

1.1 SSD优缺点

• 对于Faster R-CNN，其先通过CNN得到候选框，然后再进行分类与回归，而Yolo与SSD可以一步到位完成检测
• 相比Yolo，SSD采用CNN来直接进行检测，而不是像Yolo那样在全连接层之后做检测
• SSD提取了不同尺度的特征图来做检测，大尺度特征图（较靠前的特征图）可以用来检测小物体，而小尺度特征图（较靠后的特征图）用来检测大物体
• SSD采用了不同尺度和长宽比的先验框（Prior boxes, Default boxes，在Faster R-CNN中叫做锚，Anchors）

2. SSD 原理

SSD其基本结构如下图所示。

图2.1 SSD网络结构

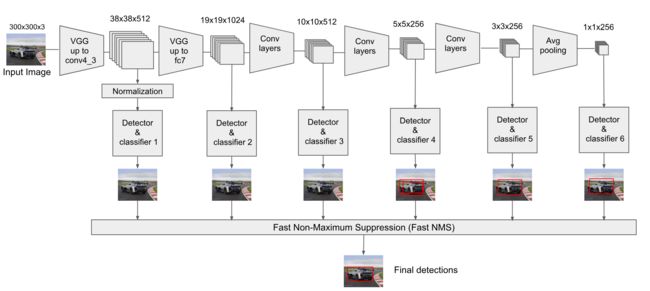
2.1 采用多尺度特征图用于检测

如上如所示，VGG网络的多个特征图都用于检测，这样做的好处是比较大的特征图来用来检测相对较小的目标，而小的特征图负责检测大目标。此外，与Yolo最后采用全连接层不同，SSD直接采用卷积对不同的特征图来进行提取检测结果。对于形状为 $m\times n\times p$ 的特征图，只需要采用 $3\times 3\times p$ 这样比较小的卷积核得到检测值

2.2 设置先验框

SSD借鉴了Faster R-CNN中anchor的理念，每个单元设置尺度或者长宽比不同的先验框，预测的边界框（bounding boxes）是以这些先验框为基准的，在一定程度上减少训练难度。一般情况下，每个单元会设置多个先验框，其尺度和长宽比存在差异如下图所示

图2.2 先验框示意图

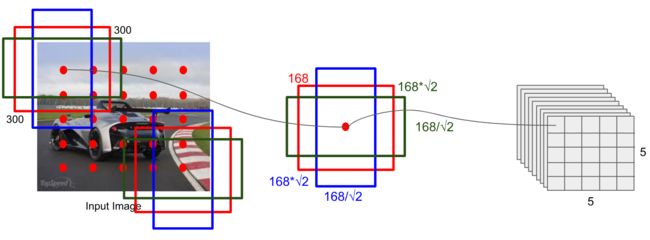
对于每个单元的每个先验框，其都输出一套独立的检测值，对应一个边界框，主要分为两个部分。

• 第一部分是各个类别的置信度或者评分，SSD将背景也当做了一个特殊的类别，如果检测目标共有 $c$ 个类别，SSD其实需要预测 $c+1$ 个置信度值，其中第一个置信度指的是不含目标或者属于背景的评分。后面当我们说 $c$ 个类别置信度时，里面是包含背景那个特殊的类别，即真实的检测类别只有 $c-1$ 个。在预测过程中，置信度最高的那个类别就是边界框所属的类别，特别地，当第一个置信度值最高时，表示边界框中并不包含目标。
• 第二部分就是边界框的 location，包含4个值 $(c_x,c_y,w,h)$ ，分别表示边界框的中心坐标以及宽和高。但是真实预测值其实只是边界框相对于先验框的偏移值(offset)。

先验框位置用 $d=(d^{cx},d^{cy},d^w,d^h)$表示，其对应边界框用 $b=(b^{cx},b^{cy},b^w,b^h)$表示，那么模型输出的预测值 $l$ 其实是 $b$ 相对于 $d$ 的偏移值：

$$\begin{array}{rl}& l^{cx}=(b^{cx}-d^{cx})/d^w\\ & l^{cy}=(b^{cy}-d^{cy})/d^h\\ & l^w=log(b^w/d^w)\\ & l^h=log(b^h/d^h)\end{array}$$

上面这个过程为边界框的编码（encode），预测时需要反向这个过程，即进行解码（decode），从预测值 $l$ 中得到边界框的真实位置 $b$。
$$\begin{array}{rl}& b^{cx}=l^{cx}{d}^w+d^{cx}\\ & b^{cy}=l^{cy}{d}^h+d^{cy}\\ & b^w=exp(l^w)d^w\\ & b_h=exp(l^h)d^h\end{array}$$

在实际的SSD实现中设置了variance超参数来调整检测值。通过bool参数variance_encoded_in_target来控制两种模式，当其为True时，表示variance被包含在预测值中，就是上面那种情况。但是如果是False（一般采用这种方式），就需要手动设置超参数variance通常设置为[0.1, 0.1, 0.2, 0.2]，用来对 $l$ 的4个值进行放缩，此时边界框的编码为

$$\begin{array}{rl}& l^{cx}=(b^{cx}-d^{cx})/(d^w\ast variance[0])\\ & l^{cy}=(b^{cy}-d^{cy})/(d^h\ast variance[1])\\ & l^w=log(b^w/d^w)/variance[2]\\ & l^h=log(b^h/d^h)/variance[3]\end{array}$$

如上式所示，计算loss时 $l^{cx},l^{cy},l^w,l^h$ 分别除以variance，这样可以增大loss，也就增加了梯度，让网络更好的学习。同理可得，此时边界框需要这样解码:

$$\begin{array}{rl}& b^{cx}=(l^{cx}\ast variance[0])d^w+d^{cx}\\ & b^{cy}=(l^{cy}\ast variance[1])d^h+d^{cy}\\ & b^w=exp(l^w\ast variance[2])d^w\\ & b_h=exp(l^h\ast variance[3])d^h\end{array}$$

综上所述，对于一个大小 $m\times n$ 的特征图，共有 $mn$ 个单元，每个单元设置的先验框数目记为 $k$ ，那么每个单元共需要 $(c+4)k$ 个预测值（每个框都有c个类别和四个定位值），所有的单元共需要 $(c+4)kmn$ 个预测值，由于SSD采用卷积做检测，所以就需要 $(c+4)k$ 个卷积核完成这个特征图的检测过程。

2.3 先验框scale缩放比例

SSD的整体网络结构如图2.1所示，分别使用conv4_3，Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2作为检测所用的特征图，共提取了6个特征图，其大小分别是 $(38,38),(19,19),(10,10),(5,5),(3,3),(1,1)$ ，不同特征图上设置的先验框尺寸是不同的。先验框的设置，包括尺度（或者说大小）和长宽比两个方面。对于先验框的尺度，其遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加。

如下图所示越往后边的特征层，它的格子数目越少，每个格子的感受野更大，也就是对应到原图的框就更大，也就是检测的物体就更大。要得到图（a）中的先验框，先通过计算不同层的缩放比获得每一特征层的基础$s_k$值，然后通过不同的长宽比和$s_k$计算真实的长宽应该是多少

图2.3 先验框设置

$s_k$的计算如下所示

$$s_k=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1),k\in \left[1,m\right]$$

其中 $m$ 指的特征图个数，实际为5 ，因为第一层（Conv4_3层）是单独设置的， $s_k$ 表示先验框大小相对于图片的比例，而 $s_{min}$ 和 $s_{max}$ 表示比例的最小值与最大值，paper里面取0.2和0.9。对于第一个特征图，其先验框的尺度比例一般设置为 $s_{min}/2=0.1$ 那么尺度为 $0.1\times 300=30$（此处按输入图片为300*300） 。对于后面的特征图，先验框尺度按照上面公式线性增加，但是实际上是先将尺度比例 $s$ 先扩大100倍，此时增长步长为 $s_{k+1}-s_k=\lfloor \frac{\lfloor s_{\max }\times 100\rfloor -\lfloor s_{\min }\times 100\rfloor }{m-1}\rfloor =17$（注意：方括号代表向下取整），那么$s_k=20+17(k-1)$，可以得到 $s_k$ 的取值为 20， 37， 54， 71，88。将这些比例除以100得到真实scales列表为[0.1,0.2,0.37,0.54,0.71,0.88,1.05]，这里可以发现由于取整的原因，并没有我们设定的0.9这个 $s_{max}$值。而之所以会出现第7个值1.05是为了之后计算长宽比时候的需要。然后再乘以图片大小，可以得到各个特征图的先验框尺度为[30, 60, 111, 162, 213, 264]。

2.4 先验框宽高比 aspect ratio

从图 2.3(a) 可以看出为了适应不同的目标我们需要设置不同的长宽比。每个特征层的每个格要是4个bbox，这里每个特征层里的所有框的scale（缩放比）是相同的，不同的便是他们的长宽比不同。总体上来看一共有5种长宽比，也就是aspect ratio也叫$a_r$，分别为[1, 2, 0.5, 3, 1/3]，对于特定的长宽比，按如下公式计算先验框的宽度与高度（注意：后文中的 $s_k$ 均指的是先验框实际尺度，而不是尺度比例）

$$\begin{gathered} w_k^a=s_k\sqrt{a_r}, \\ {h}_k^a=s_k/\sqrt{a_r} \end{gathered}$$

默认情况下，每个特征图会有一个 $a_r=1$ 且尺度为 $s_k$ 的先验框，除此之外，还会设置一个尺度为 $s_k^{\prime }=\sqrt{s_k\ast s_{k+1}}$ 且 $a_r=1$ 的先验框，这样每个特征图都设置了两个长宽比为1但大小不同的正方形先验框。注意最后一个特征图需要参考一个虚拟 $s_{m+1}=300\times 1.05=315$ 计算 $s_m^{\prime }$。

因此，每个特征图一共有 6 个先验框，分别是2个正方形的框和4个宽高比分别为{2，1/2，3，1/3} 的长方形框，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为 {3, 1/3} 的先验框。

综上2.2和2.3章节所述，当输入图大小为300*300时，得到如下结论：

• 各个特征层缩放比scale的取值分别为：[0.1,0.2,0.37,0.54,0.71,0.88,1.05] (最后一个只是为了后续计算)
• 各个特征层的先验框尺度$s_k=\text{image\_size}\ast \text{scale}$ 分别为 [30, 60, 111, 162, 213, 264, 315] （最后一个只是为了后续计算）
• 每个特征层的先验框的宽高比$a_r$为[1', 1, 2, 0.5, 3, 1/3]（1’是特殊$s_k$的情况）

下面将以Conv4_3和Conv11_2特征图为例，计算其中6个先验框(在原图上)的尺寸， Conv4_3的先验框计算如下

• $a_r=1$，$s_k^{\prime }=\sqrt{s_k\ast s_{k+1}}=\lfloor \sqrt{(30\ast 60)}\rfloor =42$时，$w=42\ast \sqrt{1}=42,h=42/\sqrt{1}=42$
• $a_r=1$，$s_k=30$时，$w=h=30$
• $a_r=0.5$, $s_k=30$时，$w=30\ast \sqrt{0.5}=21，h=30/\sqrt{0.5}=42$
• $a_r=2$, $s_k=30$时，$w=30\ast \sqrt{2}=42，h=30/\sqrt{2}=21$
• $a_r=1/3$, $s_k=30$时，$w=30\ast \sqrt{1/3}=17，h=30/\sqrt{1/3}=51$
• $a_r=3$, $s_k=30$时，$w=30\ast \sqrt{3}=51，h=30/\sqrt{3}=17$

因此最后bbox的6种长宽为[[30,30],[42,42],[42,21],[21,42],[17,51],[51,17]]（注意：上文已经提到过实际过程种Conv4_3特征层仅使用4个先验框，它们不使用长宽比为 {3, 1/3} 的先验框，此处还是计算了，主要是为了演示计算过程）

Conv11_2的先验框计算如下

• $a_r=1$，$s_k^{\prime }=\sqrt{s_k\ast s_{k+1}}=\lfloor \sqrt{(264\ast 315)}\rfloor =288$时，$w=288\ast \sqrt{1}=288,h=288/\sqrt{1}=288$
• $a_r=1$，$s_k=264$时，$w=h=264$
• $a_r=0.5$, $s_k=264$时，$w=264\ast \sqrt{0.5}=186，h=264/\sqrt{0.5}=373$
• $a_r=2$, $s_k=264$时，$w=264\ast \sqrt{2}=373，h=264/\sqrt{2}=186$
• $a_r=1/3$, $s_k=264$时，$w=264\ast \sqrt{1/3}=152，h=264/\sqrt{1/3}=457$
• $a_r=3$, $s_k=264$时，$w=264\ast \sqrt{3}=457，h=264/\sqrt{3}=152$

可以看到越到后面的检测框越大

2.5 先验框中心点

每个单元的先验框的中心点分布在各个单元的中心，即 $\left(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|}\right),i,j\in \left[0,\left|f_k\right|\right)$ ，其中 $|f_k|$
为特征图的大小，这是特征图上的中心点，我们需要将其映射到原始图片上，这里我们使用两个参数，step和offset。

• step 相当于是不同的先验框中心点的距离， step取值为 [8, 16, 32, 64, 100, 300]
• offset 相当于是左上第一个先验框的位置，其他点的位置都基于该点进行平移, offset的取值为0.5

那么特征图第一个像素点的位置对应到原图中为(0.5*8, 0.5*8)=(4, 4)。直觉上先验框的中心点应该就是映射图的相应格的中心点，所以对于conv4_3(38, 38)，那么每个格的step应该四舍五入后300//38=8，在前几层step的确是这样设置的。但是我们发现在第三层开始这样计算后的值应该是30而不是32, 64应该是60，这里一个比较好的解释是首先这里的偏移量很小，一个是2一个是4，而且先验框只是一个设置的框，最后会通过lx,ly,lw,lh通过偏移再得到真实的值，所以偏差一点并没有太大的问题，同时这些值为8的倍数，在底层硬件处理上会可以得到更好的优化。而到了更大的尺寸100和300，如果还使用8的倍数，这样会让偏差过大。

综上，将特征图中的中心点映射到原图中得到的中心点坐标应该为：
$$\left(\frac{i+0.5}{\left|f_k\right|}\ast \text{image\_size[0]}，\frac{j+0.5}{\left|f_k\right|}\ast \text{image\_size[1]}\right),i,j\in \left[0,\left|f_k\right|\right)$$

2.6 构建先验框

通过VGG网络得到了特征图之后，需要对特征图进行卷积得到检测结果，下图给出了一个 $5\times 5$ 大小的特征图的检测过程。

其中Priorbox是根据前面介绍的生成规则得到先验框。检测值包含两个部分：类别置信度和边界框位置，各采用一次 $3\times 3$ 卷积来进行完成。由于每个先验框都会预测一个边界框，所以SSD300一共可以预测 $38\ast 38\ast 4+19\ast 19\ast 6+10\ast 10\ast 6+5\ast 5\ast 63\ast 3\ast 4+1\ast 1\ast 4=8732$个边界框。

name	Out_size	Prior_box_num	Total_num
conv4_3	38x38	4	5776
conv7（fc7）	19x19	6	2166
conv8_2	10x10	6	600
conv9_2	5x5	6	150
conv10_2	3x3	4	36
conv11_2	1x1	4	4
			8732

3. 训练

上文中提到过，模型的输出是先验框和真实边界框的偏移值，这一点非常重要！

3.1 先验框匹配

在训练过程中，首先要确定训练图片中的ground truth（真实边界框）与哪个先验框来进行匹配。SSD的先验框与ground truth的匹配原则主要有两点。

• 对于图片中每个ground truth，找到与其IOU最大的先验框，该先验框与其匹配，这样可以保证每个ground truth一定与某个先验框匹配。通常称与ground truth匹配的先验框为正样本，反之，若一个先验框没有与任何ground truth进行匹配，那么该先验框只能与背景匹配，就是负样本。
• 一个图片中ground truth是非常少的， 而先验框却很多，如果仅按第一个原则匹配，很多先验框会是负样本，正负样本极其不平衡，所以需要第二个原则。第二个原则是：对于剩余的未匹配先验框，若与某个ground truth的 IOU 大于某个阈值（一般是0.5），那么该先验框也与这个ground truth进行匹配。这意味着某个ground truth可能与多个先验框匹配，但是反过来却不可以，因为一个先验框只能匹配一个ground truth，如果多个ground truth与某个先验框 IOU 大于阈值，那么先验框只与IOU最大的那个ground truth进行匹配。

注意：第二个原则一定在第一个原则之后进行，仔细考虑一下这种情况，如果某个ground truth所对应最大 IOU 小于阈值，并且所匹配的先验框却与另外一个ground truth的 IOU 大于阈值，那么该先验框应该匹配前者，首先要确保某个ground truth一定有一个先验框与之匹配。但是，这种情况我觉得基本上是不存在。由于先验框很多，某个ground truth的最大 IOU 肯定大于阈值，所以可能只实施第二个原则既可以了。

3.2 困难负样本挖掘

尽管一个ground truth可以与多个先验框匹配，但是ground truth相对先验框还是太少了，所以负样本相对正样本会很多。为了保证正负样本尽量平衡，SSD采用了hard negative mining，就是对负样本进行抽样，抽样时按照置信度误差（预测背景的置信度越小，误差越大）进行降序排列，选取误差的较大的top-k作为训练的负样本，以保证正负样本比例接近1:3。

3.3 损失函数

损失函数定义为位置误差（locatization loss， loc）与置信度误差（confidence loss, conf）的加权和：

$$L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g))$$

权重系数 $\alpha$ 通过交叉验证设置为1

3.3.1 位置偏移损失

上式中 $N$ 是先验框的正样本数量，其中位置误差$L_{loc}$具体定义如下：

$$L_{loc}(x,l,g)=\sum _{i\in pos}^N\sum _{m\in \{cx,cy,w,h\}}{x}_{ij}^k{\mathrm{smooth}}_{L1}(l_i^m-{\hat{g}}_j^m)$$

这里面
$$\begin{array}{rl}& {\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \mathrm{if}|x|<1\\ |x|-0.5& \mathrm{otherwise},\end{array}\\ & {\hat{g}}_j^{cx}=(g_j^{cx}-d_i^{cx})/d_i^w\\ & {\hat{g}}_j^{cy}=(g_j^{cy}-d_i^{cy})/d_i^h\\ & {\hat{g}}_j^w=\log \left(\frac{g_j^w}{d_i^w}\right)\\ & {\hat{g}}_j^h=\log \left(\frac{g_j^h}{d_i^h}\right)\end{array}$$
其中 $x_{ij}^k\in \{0,1\}$ 为一个指示参数，当 $x_{ij}^k=1$ 时表示第 $i$ 个先验框与第 $j$ 个ground truth匹配，并且ground truth的类别为 $k$ 。 $l$ 为先验框与grounding truth bbox的模型预测的偏移值。而 $g$ 是ground truth的位置参数，$d$是先验框的位置参数，通过$g$和$d$可以算出先验框和grounding truth bbox的真实位置偏移 $\hat{g}$ 。即位置误差损失就是模型预测的位置偏移和真实位置偏移的 $smoot{h}_{L1}$损失。

由于 $x_{ij}^k$ 的存在，所以位置误差仅针对正样本进行计算。值得注意的是，要先对ground truth的
进行编码得到 $\hat{g}$ ，因为预测值 $l$ 是在特征图上预测的，也是编码值。如上文中公式（9）到公式（12）所示，若设置了variance，编码时要加上variance，如下式所示，此处只计算了 ${\hat{g}}_j^{cx}$ 其他三个按类似方式计算。

$${\hat{g}}_j^{cx}=(g_j^{cx}-d_i^{cx})/d_i^w/variance[0]$$

3.3.2 置信度损失

对于置信度误差，采用了softmax loss，即一个多分类问题。

$$L_{conf}(x,c)=-\sum _{i\in \mathcal{P}\circ s}^N{x}_{ij}^{p}log({\hat{c}}_i^p)-\sum _{i\in Neg}log({\hat{c}}_i^0)\mathrm{where}{\hat{c}}_i^p=\frac{\exp (c_i^p)}{{\sum }_p\exp (c_i^p)}$$

3.4 训练部分小结

训练的总体流程如下图所示

图中的default boxes也就是我们所说的先验框，jaccard overlap 计算（Jacard重叠）其实就是 IOU 的计算，其示意图如下
SSD整体的的步骤如下：
（1）通过2.4章节所述方式构建先验框
（2）通过计算 jaccard overlap 找出与grounding truth 对应的先验框，确定正负样本
（3）计算损失，训练模型，修正模型的预测偏移值
（4）训练完毕，推理阶段，模型先预测出偏移值，然后通过公式（5）到（8）推理出目标框的位置

4. 数据增强

以上部分便是SSD的原理，通过上面的章节即可了解SSD的训练过程。在SSD中还通过数据增强来提高模型的泛化能力，此处不在将讲解，其与原理无太大关系，且与其他模型的数据增强基本一致。

了解更多AI算法（CV NLP AIGC LLM）关注 微信公众号 funNLPer

本文主要讲解SSD的原理，并未涉及代码，下一篇博文将结合人脸检测从代码中来深入来了解SSD目标检测

5. 参考

• 目标检测|SSD原理与实现-知乎
• SSD算法详解-CSDN
• SSD: Single Shot MultiBox Detector-在线ppt
• SSD Single Shot MultiBox Detector-deepsystems.io
• 大白话分析——SSD目标检测网络从训练到预测（上）
• 目标识别网络SSD：Pytorch源码分析（一）