数据结构基础：P11.3-散列查找---＞冲突处理方法

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-线性结构—＞应用实例：多项式加法运算
数据结构基础：P2.5-线性结构—＞应用实例：多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构
数据结构基础：P3.3-树(一)—＞二叉树的遍历
数据结构基础：P3.4-树(一)—＞小白专场：树的同构-C语言实现
数据结构基础：P4.1-树(二)—＞二叉搜索树
数据结构基础：P4.2-树(二)—＞二叉平衡树
数据结构基础：P4.3-树(二)—＞小白专场：是否同一棵二叉搜索树-C实现
数据结构基础：P4.4-树(二)—＞线性结构之习题选讲：逆转链表
数据结构基础：P5.1-树(三)—＞堆
数据结构基础：P5.2-树(三)—＞哈夫曼树与哈夫曼编码
数据结构基础：P5.3-树(三)—＞集合及运算
数据结构基础：P5.4-树(三)—＞入门专场：堆中的路径
数据结构基础：P5.5-树(三)—＞入门专场：File Transfer
数据结构基础：P6.1-图(一)—＞什么是图
数据结构基础：P6.2-图(一)—＞图的遍历
数据结构基础：P6.3-图(一)—＞应用实例：拯救007
数据结构基础：P6.4-图(一)—＞应用实例：六度空间
数据结构基础：P6.5-图(一)—＞小白专场：如何建立图-C语言实现
数据结构基础：P7.1-图(二)—＞树之习题选讲：Tree Traversals Again
数据结构基础：P7.2-图(二)—＞树之习题选讲：Complete Binary Search Tree
数据结构基础：P7.3-图(二)—＞树之习题选讲：Huffman Codes
数据结构基础：P7.4-图(二)—＞最短路径问题
数据结构基础：P7.5-图(二)—＞哈利·波特的考试
数据结构基础：P8.1-图(三)—＞最小生成树问题
数据结构基础：P8.2-图(三)—＞拓扑排序
数据结构基础：P8.3-图(三)—＞图之习题选讲-旅游规划
数据结构基础：P9.1-排序(一)—＞简单排序(冒泡、插入)
数据结构基础：P9.2-排序(一)—＞希尔排序
数据结构基础：P9.3-排序(一)—＞堆排序
数据结构基础：P9.4-排序(一)—＞归并排序
数据结构基础：P10.1-排序(二)—＞快速排序
数据结构基础：P10.2-排序(二)—＞表排序
数据结构基础：P10.3-排序(二)—＞基数排序
数据结构基础：P10.4-排序(二)—＞排序算法的比较
数据结构基础：P11.1-散列查找—＞散列表
数据结构基础：P11.2-散列查找—＞散列函数的构造方法

---

一、开放定址法

散列查找的冲突处理方法冲突处理的方法有两种常见的思路

①换个位置存放：开放地址法
②同一位置的冲突对象组织在一起：链地址法(把有冲突的对象都放在一个链表里面)

开放定址法(Open Addressing)

①一旦产生了冲突(该地址已有其它元素)，就按某种规则去寻找另一个空地址。若发生了第i次冲突，下一个地址将试探性地增加 ${\mathrm{d}}_{\mathrm{i}}$，基本公式是：${\mathrm{h}}_{\mathrm{i}}(\mathrm{k}\mathrm{e}\mathrm{y})=(\mathrm{h}(\mathrm{k}\mathrm{e}\mathrm{y})+{\mathrm{d}}_{\mathrm{i}})\%\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}(1\le \mathrm{i}<\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e})$
② ${\mathrm{d}}_{\mathrm{i}}$ 决定了不同的解决冲突方案：线性探测、平方探测、双散列。
线性探测：${\mathrm{d}}_{\mathrm{i}}=\mathrm{i}$，实际上就是往后面一个个找
平方探测：${\mathrm{d}}_{\mathrm{i}}=\pm {\mathrm{i}}^2$，朝两个方向找
双散列：$\mathrm{d}\mathrm{i}=\mathrm{i}\ast {\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})$，再设计一个散列函数，让i乘上它得到地址的偏移量

二、线性探测

线性探测法：以增量序列1,2,……,(TableSize -1)循环试探下一个存储地址。

例子：

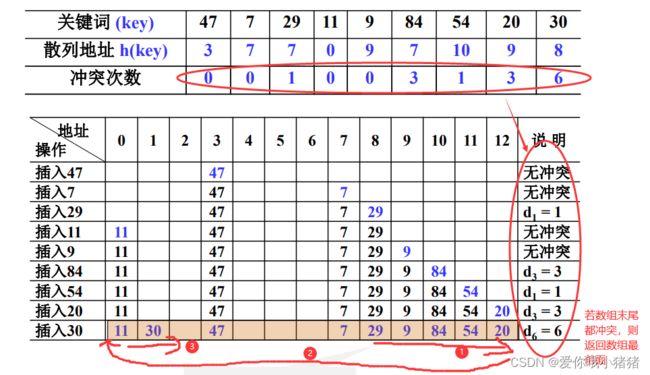
题目描述：设关键词序列为 {47，7，29，11，9，84，54，20，30}，
散列表的表长TableSize =13 (装填因子 α = 9/13 ≈ 0.69)；
散列函数为：H(key) = key mod 11。
用线性探测法处理冲突，列出依次插入后的散列表，并估算查找性
思路：
我们算一下这9个元素所相应的散列函数的值

接着，我们依次将各个关键词插入对应的地方。如果有冲突，则根据冲突次数往后挪动对应的位数。如果一直到数组末尾都还冲突，则返回数组最前面继续往后找。

分析：在这里面我们注意到一个现象：当我们的散列值算出来有冲突集中在某些位置的时候，在这个位置会形成聚集。即这个地方的冲突会越来越多，这就是线性探测的一个问题，会形成聚集现象。

散列表查找性能分析

散列查找的效率主要就是看它的平均查找的次数，或者叫平均查找的长度(ASL)，平均查找长度又分为两种：
①成功平均查找长度(ASLs)：把散列表的每个元素去算算看，我为了找它需要找几次，然后平均值一算就是成功的平均查找长度
②不成功平均查找长度 (ASLu)：确认元素不在表中的平均查找次数。
例子
这是上面那个例子中我们已经构造好的一个散列表，冲突次数我们也标在这里了，我们来算一下它的平均查找长度

①ASLs：每个元素的成功查找长度=冲突次数+1。冲突次数为0，则比较1次就找到。冲突次数为6，则比较7次才找到。于是让所有冲突次数+1并累加起来求均值就得到结果。

ASLs = (1+7+1+1+2+1+4+2+4) / 9 = 23/9 ≈ 2.56
②ASLu：我们不可能枚举所有不在散列表中的元素来看它们查找不成功的查找次数。一般的方式是：将不在散列表中的元素按照关键词分若干类。在这道题中我们根据H(key)的值来分类，H(key)=key%1，结果是从0到10，共11种可能。于是对于每种结果去找它应该存储的位置，如果碰到空位了我们就断定了它一定不在这里面，因为如果我们没有删除的操作发生，他就不应该碰到空位。

ASLu = (3+2+1+2+1+1+1+9+8+7+6) / 11 = 41/11 ≈ 3.73

三、线性探测-字符串的例子

例子：

题目描述：将acos、define、float、exp、char、atan、ceil、floor，顺次存入一张大小为26的散列表中。H(key)=key[0]-’a’，采用线性探测 ${\mathrm{d}}_{\mathrm{i}}=\mathrm{i}$。
思路：
①我们先把不冲突的元素放进去

②接着按照有冲突就往后走的原则继续将剩余元素放进去

③ASLs = (1+1+1+1+1+2+5+3) / 8 = 15/8 ≈ 1.87，不冲突的5个元素查找1次就找到，另外三个冲突的元素分别查找2、5、7次找到，如下图所示：

④ASLu：根据H(key)值分为26种情况：H值为0,1,2,…,25，求出每一类情况要找的次数，结果如下：

ASLu= (9+8+7+6+5+4+3+2+1*18) / 26 = 62/26 ≈ 2.38

四、平方探测法

平方探测法：以增量序列 $1^2,-1^2,2^2,-2^2,......,{\mathrm{q}}^2,-{\mathrm{q}}^2$，且 $\mathrm{q}\le \lfloor \mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}/2\rfloor$ 循环试探下一个存储地址。

例子：

题目描述：
设关键词序列为 {47，7，29，11，9，84，54，20，30}，
散列表表长：TableSize = 11，
散列函数为：H(key) = key mod 11。
用平方探测法处理冲突，列出依次插入后的散列表，并估算ASLs。
思路：
①首先求出各个元素应该在的位置

②接着按照平方探测法的思路去处理冲突的情况，最终元素的存储如下：

③成功平均查找长度直接将各冲突次数+1并累加起来求均值即可。ASLs = (1+1+2+1+1+3+1+4+4) / 9 = 18/9 = 2

分析：

问题：虽然表里有空间，但是平方探测(二次探测)找不到
例子：这里有如下的散列表，且散列函数也已经给出。

假设现在我要插入11这个元素，我们可以发现它一直插不进去，在0和2之间一直来回跳。

解决方案：有定理显示如果散列表长度TableSize是某个4k+3(k是正整数)形式的素数时，平方探测法就可以探查到整个散列表空间。
优点：解决了线性探测的空间聚集的缺点。

五、平方探测法的实现

散列表可以设计成一个结构HashTbl，里面有两个分量：分量cell是个数组，分量TableSize代表当前表的实际大小。

typedef struct
HashTbl *HashTable;
struct HashTbl{
	int TableSize;
	Cell *TheCells;
}H ; 

HashTable InitializeTable( int TableSize )
{
	HashTable H;
	int i;
	if ( TableSize < MinTableSize ){
		Error( "散列表太小" );
		return NULL;
	}
	/* 分配散列表 */
	H = (HashTable)malloc( sizeof( struct HashTbl ) );
	if ( H == NULL )
		FatalError( "空间溢出!!!" );
	//找一个素数，防止表里有空间但是找不到
	H->TableSize = NextPrime( TableSize );
	/* 分配散列表 Cells */
	H->TheCells=(Cell *)malloc(sizeof( Cell )*H->TableSize);
	if( H->TheCells == NULL )
		FatalError( "空间溢出!!!" );
	//将cell做成一个结构，里面包含Element和info，使用info标记状态，Element存放数据
	for( i = 0; i < H->TableSize; i++ )
		H->TheCells[ i ].Info = Empty;
	return H;
}

代码中，Cell这个数组设置为结构数组，其结构如下图所示：

Cell设置为结构数组的原因如下：

我们前面都讨论了往表里面插入元素，也讨论了在这个表里面怎么找元素，我们还没谈到过怎么删除元素。实际上删除元素时，你不能真的把这个元素从这个表里拿掉。拿掉了之后，我们查找的时候会有问题的。如果我把一个元素删除，我仍然放在哈希表里面，我给他做个记号这个记号就说这个元素被删掉了，他对我们后面的查找跟插入有好处：
①首先，我查找的时候碰到被删掉的元素，这个位置做了个记号说被删掉了，我就知道现在还不是空位，还可以继续找。如果你真的把他拿掉了变成空位了，我就会产生误判。
②然后，我插入的时候发现这个元素被删掉了，他不是空位，是原来有元素占着的，现在被删掉了。所以这个时候我插入元素，就可以来替代原来删掉的元素。所以这样的话，我们插入删除操作都可以做，而且不影响我们的查找过程。
③所以这里面我们有种需，求对每个元素有个记号说明他是什么状态。所以我们用个结构，这个结构包含两个东西，一个时Info，另一个就是我们的 data。一开始的时候，表里面每个元素都是空的，所以初始化为Empty

查找操作的代码如下：

Position Find( ElementType Key, HashTable H ) /*平方探测*/
{ 
	Position CurrentPos, NewPos;
	int CNum; /* 记录冲突次数 */
	CNum = 0;
	NewPos = CurrentPos = Hash( Key, H->TableSize ); 
	while( H->TheCells[ NewPos ].Info != Empty && H->TheCells[ NewPos ].Element != Key ) {
	/* 字符串类型的关键词需要 strcmp 函数!! */
		if(++CNum % 2){ /* 判断冲突的奇偶次，奇数就加上平方 */ 
			NewPos = CurrentPos + (CNum+1)/2*(CNum+1)/2;
			while( NewPos >= H->TableSize )
				NewPos -= H->TableSize;
		} else { //偶数就减去平方
			NewPos = CurrentPos - CNum/2 * CNum/2;
			while( NewPos < 0 )
				NewPos += H->TableSize;
		}
	}
	return NewPos;
}

在代码中，根据冲突的次数来找位置，我们不用CurrentPos±i，而使用了CurrentPos + (CNum+1)/2*(CNum+1)/2，这样做是为了做一个映射，方便Cnum的存储。

插入操作代码如下：

void Insert( ElementType Key, HashTable H )
{ /* 插入操作 */
	Position Pos;
	Pos = Find( Key, H );
	if( H->TheCells[ Pos ].Info != Legitimate ) {
		/* 确认在此插入 */
		H->TheCells[ Pos ].Info = Legitimate;
		H->TheCells[ Pos ].Element = Key;
		/*字符串类型的关键词需要 strcpy 函数!! */
	 }
}

在代码中，我们使用了一种懒惰删除

在开放地址散列表中，删除操作要很小心，通常只能“懒惰删除”，即需要增加一个“删除标记(Deleted)”，而并不是真正删除它。 以便查找时不会“断链”。其空间可以在 下次插入时重用。

双散列探测法(Double Hashing)

①双散列探测法: ${\mathrm{d}}_{\mathrm{i}}$ 为 $\mathrm{i}\ast {\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})$，$\mathrm{i}\ast {\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})$ 是另一个散列函数。探测序列成：${\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})$，$2{\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})$，$3{\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})...$
②对任意的key，${\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})\ne 0$
③探测序列还应该保证所有的散列存储单元都应该能够被探测到。选择以下形式有良好的效果：
${\mathrm{h}}_2(\mathrm{k}\mathrm{e}\mathrm{y})=\mathrm{p}-(\mathrm{k}\mathrm{e}\mathrm{y}\%\mathrm{p})$
④其中：$\mathrm{p}<\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e},\mathrm{p}和\mathrm{T}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{S}\mathrm{i}\mathrm{z}\mathrm{e}$都是素数。

再散列

当散列表元素太多(即装填因子 α太大)时，查找效率会下降；
当装填因子过大时，解决的方法是加倍扩大散列表，这个过程叫做再散列(Rehashing)。实用最大装填因子一般取 0.5 <= α<= 0.85
散列表扩大时，原有元素需要重新计算放置到新表中

六、分离链接法

我们前面提到过一种思想，把所有有冲突的元素全部串在一起。比方说我们的2号位置需要放三个元素，我们就把这三个元素用链表串在一起。在2号位置上面有个指针，指向这样的一个链表。所以这种方法呢叫分离链接法

例子：

题目描述：设关键字序列为 47, 7, 29, 11, 16, 92, 22, 8, 3, 50, 37, 89, 94, 21。散列函数取为：h(key) = key mod 11。用分离链接法处理冲突。
思路：按照分离链接法的思路，将冲突元素用链表连接起来，这14个元素在数组中的存储如下：

表中有9个结点只需1次查找，5个结点需要2次查找，查找成功的平均查找次数： ASLs=(9+5*2) / 14 ≈ 1.36

对应代码如下：

typedef struct ListNode *Position, *List;
struct ListNode {
	ElementType Element;
	Position Next;
};
typedef struct HashTbl *HashTable; 
struct HashTbl {
	int TableSize;
	List TheLists;
};
Position Find( ElementType Key, HashTable H )
{ 
	Position P;
	int Pos;
	Pos = Hash( Key, H->TableSize ); /*初始散列位置*/
	P = H->TheLists[Pos]. Next; /*获得链表头*/
	while( P != NULL && strcmp(P->Element, Key) )
		P = P->Next;
	return P;
}

C语言代码：创建开放定址法的散列表

#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType;    /* 关键词类型用整型 */
typedef int Index;          /* 散列地址类型 */
typedef Index Position;     /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型，分别对应：有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;

typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{
    ElementType Data; /* 存放元素 */
    EntryType Info;   /* 单元状态 */
};

typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    Cell *Cells;   /* 存放散列单元数据的数组 */
};

int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */
    int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */

    while( p <= MAXTABLESIZE ) {
        for( i=(int)sqrt(p); i>2; i-- )
            if ( !(p%i) ) break; /* p不是素数 */
        if ( i==2 ) break; /* for正常结束，说明p是素数 */
        else  p += 2; /* 否则试探下一个奇数 */
    }
    return p;
}

HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;

    H = (HashTable)malloc(sizeof(struct TblNode));
    /* 保证散列表最大长度是素数 */
    H->TableSize = NextPrime(TableSize);
    /* 声明单元数组 */
    H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
    /* 初始化单元状态为“空单元” */
    for( i=0; i<H->TableSize; i++ )
        H->Cells[i].Info = Empty;

    return H;
}

C语言代码：平方探测法的查找和插入

Position Find( HashTable H, ElementType Key )
{
    Position CurrentPos, NewPos;
    int CNum = 0; /* 记录冲突次数 */

    NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    /* 当该位置的单元非空，并且不是要找的元素时，发生冲突 */
    while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {
                                           /* 字符串类型的关键词需要 strcmp 函数!! */
        /* 统计1次冲突，并判断奇偶次 */
        if( ++CNum%2 ){ /* 奇数次冲突 */
            NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */
            if ( NewPos >= H->TableSize )
                NewPos = NewPos % H->TableSize; /* 调整为合法地址 */
        }
        else { /* 偶数次冲突 */
            NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */
            while( NewPos < 0 )
                NewPos += H->TableSize; /* 调整为合法地址 */
        }
    }
    return NewPos; /* 此时NewPos或者是Key的位置，或者是一个空单元的位置（表示找不到）*/
}

bool Insert( HashTable H, ElementType Key )
{
    Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */

    if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占，说明Key可以插入在此 */
        H->Cells[Pos].Info = Legitimate;
        H->Cells[Pos].Data = Key;
        /*字符串类型的关键词需要 strcpy 函数!! */
        return true;
    }
    else {
        printf("键值已存在");
        return false;
    }
}

C语言代码：分离链接法的散列表实现

#define KEYLENGTH 15                   /* 关键词字符串的最大长度 */
typedef char ElementType[KEYLENGTH+1]; /* 关键词类型用字符串 */
typedef int Index;                     /* 散列地址类型 */
/******** 以下是单链表的定义 ********/
typedef struct LNode *PtrToLNode;
struct LNode {
    ElementType Data;
    PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/******** 以上是单链表的定义 ********/

typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    List Heads;    /* 指向链表头结点的数组 */
};

HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;

    H = (HashTable)malloc(sizeof(struct TblNode));
    /* 保证散列表最大长度是素数，具体见代码5.3 */
    H->TableSize = NextPrime(TableSize);

    /* 以下分配链表头结点数组 */
    H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));
    /* 初始化表头结点 */
    for( i=0; i<H->TableSize; i++ ) {
         H->Heads[i].Data[0] = '\0';
         H->Heads[i].Next = NULL;
    }

    return H;
}

Position Find( HashTable H, ElementType Key )
{
    Position P;
    Index Pos;
    
    Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 */
    /* 当未到表尾，并且Key未找到时 */ 
    while( P && strcmp(P->Data, Key) )
        P = P->Next;

    return P; /* 此时P或者指向找到的结点，或者为NULL */
}

bool Insert( HashTable H, ElementType Key )
{
    Position P, NewCell;
    Index Pos;
    
    P = Find( H, Key );
    if ( !P ) { /* 关键词未找到，可以插入 */
        NewCell = (Position)malloc(sizeof(struct LNode));
        strcpy(NewCell->Data, Key);
        Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
        /* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
        NewCell->Next = H->Heads[Pos].Next;
        H->Heads[Pos].Next = NewCell; 
        return true;
    }
    else { /* 关键词已存在 */
        printf("键值已存在");
        return false;
    }
}

void DestroyTable( HashTable H )
{
    int i;
    Position P, Tmp;
    
    /* 释放每个链表的结点 */
    for( i=0; i<H->TableSize; i++ ) {
        P = H->Heads[i].Next;
        while( P ) {
            Tmp = P->Next;
            free( P );
            P = Tmp;
        }
    }
    free( H->Heads ); /* 释放头结点数组 */
    free( H );        /* 释放散列表结点 */
}

小测验

1、设有一组记录的关键字为 {19，14，23，1，68，20，84，27，55，11，10，79}，用分离链接法构造散列表，散列函数为H(key)= key mod 13。问：散列地址为1的链中有几个记录？

A. 1
B. 2
C. 3
D. 4

答案：D

2、设一个散列表的大小是11, 散列函数是H(key)=key mod 11. 若采用平方探测（)冲突解决方法，将4个元素{14，38，61，86}顺序插入散列表中。如果再插入元素49，则该元素将被放在什么位置？

A. 4
B. 6
C. 9
D. 10

答案：A

3、假设一散列表的大小是11,散列函数是H(key)=key mod 11，用线性探测法解决冲突。先将4个元素{14，38，61，86}按顺序插入初始为空的散列表中。如果再插入元素49，则该元素被插入到表中哪个位置（下标）？

A. 4
B. 5
C. 6
D. 7

答案：D