数据结构与算法之1——数据结构基础知识

数据结构和算法相当于兵法，如果我们常看兵法，便可做到胸有成竹，有时会事半功倍！同样，如果我们常看数据结构与算法，我们写程序时也能游刃有余、明察秋毫，遇到问题时亦能入木三分、迎刃而解.
数据结构和算法是一名程序开发人员的必备基本功，不是一朝一夕就能练成绝世高手的。冰冻三尺非一日之寒，需要我们平时不断的主动去学习积累。

算法的五大特性：

1. 输入
2. 输出
3. 有穷性：算法在有限步骤之后会自动结束，而不会无限循环，而且每一步都是在有限的时间内完成的。
4. 确定性：算法中的每一步都有确定的含义，不会出现二义性。
5. 可行性：算法的每一步骤都是可行的，也就是每一步都会执行有限的次数后完成。

算法的执行效率

我们都知道，一个算法好坏直观上都是通过算法执行的快慢来做评判的，但是如果一个算法在两台不同的机器上执行，一个机器cpu较好，一个较差，此时执行时间明显是有差异的，所以单靠执行时间来评判算法的好坏是不一定客观准确地。
假定算法执行的每一个基本操作的时间单位是固定的，那么一个算法有多少个基本操作就代表要花费多少个时间单位。所以我们可以用这种通过评判一个算法的基本操作的方法，来客观反映一个算法的时间效率，也就是“大O表示法”。

“大O记法”：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度，记为T(n)

大O表示法的理解：

对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

• 算法完成工作最少需要多少基本操作，即最优时间复杂度
• 算法完成工作最多需要多少基本操作，即最坏时间复杂度
• 算法完成工作平均需要多少基本操作，即平均时间复杂度

对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的几条基本计算规则

1. 基本操作，即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度
   比如下面这道题：
   如果 a+b+c=1000，且 a^2+b2=c²（a,b,c 为自然数），如何求出所有a、b、c可能的组合?
   第一次尝试算法核心部分：

for a in range(1001):
	for b in range(1001):
		for c in range(1001):
			if a*a+b*b==c*c and a+b+c=1000:
				print("(a,b,c:%d,%d,%d)",%(a,b,c))

时间复杂度：
T(n) = O(nnn) = O(n³)
第二次尝试：

for a in range(1001):
	for b in range(1001):
		c=1000-a-b
		if a*a + b*b =c * c:
		print("(a,b,c:%d,%d,%d)",%(a,b,c))

时间复杂度：
T(n) = O(nnn) = O(n²)

常见时间复杂度

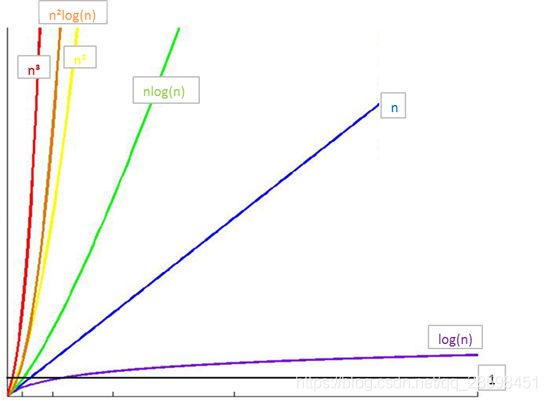
所消耗的时间从小到大：
O(1)2)2log(n)) 3)n)n)

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法
总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种：

• 插入
• 删除
• 修改
• 查找
• 排序